Solution -「NOI.AC 省选膜你赛」寄蒜几盒

题目

题意简述

  给定一个含有 \(n\) 个顶点的凸多边形（ \(n\) 是偶数），对于每一对相对的边（即中间有 \(\frac{n}2-1\) 条其它边），延长它们以将平面分割为多块，并把包含原凸包的一块染色（包含边界）。再给出 \(q\) 个询问，询问一个点 \(p\) 所在位置是否被染色。

数据规模

  强制在线，\(n,q\le10^5\)。

题解

题意转化

  首先，考虑某个点“被染色”的条件：存在一对相对边，若两边不平行，则该点在这对边延长所构成的劣角内部；若两边平行，则该点在它们所在两条直线的异侧。下图表现了第一种情况：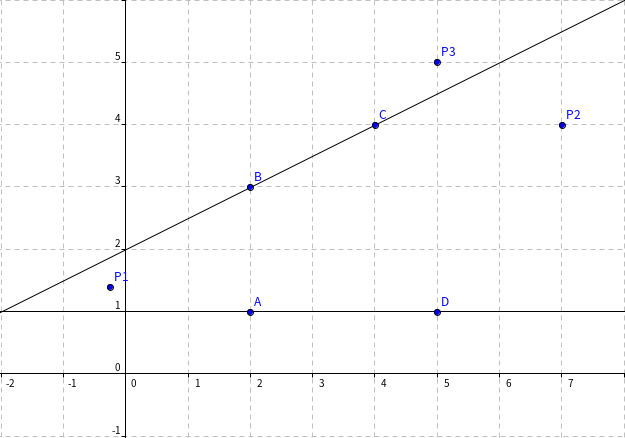

  在图中，如果我们把凸多边形（四边形 \(ABCD\)）看作障碍物，那么 \(P1\) 看不到 \(AD,BC\) 两边，\(P2\) 亦是如此，而二者都被相对边 \((AD,BC)\) 染色了。相反，对于 \(P3\)，它能看到 \(BC\) 这条边，所以没有被这对边染色。

  尝试把这个结论推广，对于任意一点 \(P\)，若存在 \(P\) 看不到的一对相对边，\(P\) 就会被染色，反之则不会被染色。所以，对于不会被染色的 \(P\)，它至少能看到多边形 \(\frac{n}2\) 条边。

算法构建

  第一步，我们要得到判断“一组相对边是否能染色某个点”的方法。还是以上图为例：

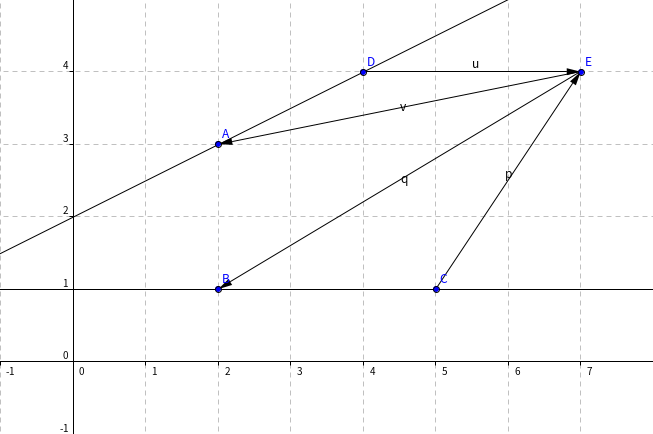
  对于 \(E\) 点，我们求出向量 \(\boldsymbol{u}=\vec{DE},\boldsymbol{v}=\vec{EA},\boldsymbol{p}=\vec{CE},\boldsymbol{q}=\vec{EB}\)（注意在这里 \(B,C,D,A\) 四点是按逆时针排列的）。并记 \(a=\boldsymbol{u}\times\boldsymbol{v},b=\boldsymbol{p}\times\boldsymbol{q}\)，可以发现，当 \((a=0\lor b=0)\lor(a<0\land b>0)\) 为真时，\(E\) 被这组边染色。

---

  第二步，还需要判断“一个点能否看到多边形上的某个点”。其实很简单，只需要令第一步中 \(D,C\) 重合，\(A,B\) 分别为多边形上的前驱和后继顶点，如第一步判断能否染色就行啦~

---

  第三步，如何求 \(P\) 能够看到几条边呢？不难想到二分：先取出一个会被看到的凸多边形上的点，再分别向两侧扩展。但怎么找到这个点呢？

  \(O(n)\) 找肯定是不可取的。我们耍一个小聪明：随便取一个点，设其在凸多边形上的下标为 \(i\)，并取出 \((i,i+1),(i+\frac{n}2,i+\frac{n}2+1)\) 这组对边，作第一步的判断。如果判断成功，就直接得出答案啦；否则，\(P\) 就一定能看到这四个点中的两个（某一条边），再用第二步的方法就可以找到我们需要的点了。

---

  最后，二分即可。

代码

#include <ctime>
#include <cstdio>
#include <cstdlib>
#include <utility>

typedef long long LL;
typedef __int128 LLL;

inline LL rint () {
	LL x = 0, f = 1; char s = getchar ();
	for ( ; s < '0' || '9' < s; s = getchar () ) f = s == '-' ? -f : f;
	for ( ; '0' <= s && s <= '9'; s = getchar () ) x = x * 10 + ( s ^ '0' );
	return x * f;
}

const int MAXN = 1e5;
int T, N, Q;

struct Point { LLL x, y; } P[MAXN + 5];

struct Vector {
	LLL x, y;
	Vector () {}
	Vector ( const Point p ): x ( p.x ), y ( p.y ) {}
	Vector ( const LLL tx, const LLL ty ): x ( tx ), y ( ty ) {}
	Vector ( const Point s, const Point t ): x ( t.x - s.x ), y ( t.y - s.y ) {}
	inline LLL operator * ( const Vector t ) const { return x * t.y - y * t.x; }
};

inline bool visible ( const Point s, const int indx ) {
	LLL t1 = Vector ( P[indx], s ) * Vector ( s, P[indx % N + 1] );
	LLL t2 = Vector ( P[indx], s ) * Vector ( s, P[( indx - 2 + N ) % N + 1] );
	bool ret = t1 > 0 || t2 < 0;
	return ret;
}

int main () {
	srand ( time ( 0 ) ^ 20120712 );
	T = rint (), N = rint ();
	for ( int i = 1; i <= N; ++ i ) P[i].x = rint (), P[i].y = rint ();
	Q = rint ();
	int cnt = 0;
	for ( Point R; Q --; ) {
		R.x = rint (), R.y = rint ();
		if ( T ) R.x ^= 1ll * cnt * cnt * cnt, R.y ^= 1ll * cnt * cnt * cnt;
		int p = rand () % N + 1, q = ( p + N / 2 - 1 ) % N + 1;
		LLL t1 = Vector ( P[p], R ) * Vector ( R, P[p % N + 1] );
		LLL t2 = Vector ( P[q % N + 1], R ) * Vector ( R, P[q] );
		if ( ! t1 || ! t2 || ( t1 < 0 && t2 > 0 ) ) {
			puts ( "DA" ), ++ cnt;
			continue;
		}
		int rpos = visible ( R, p ) ? p : q;
		int l = 0, r = N - 1, mid;
		while ( l < r ) {
			mid = l + r + 1 >> 1;
			if ( visible ( R, ( rpos - mid - 1 + N ) % N + 1 ) ) l = mid;
			else r = mid - 1;
		}
		int prelen = l;
		l = 0, r = N - 1;
		while ( l < r ) {
			mid = l + r + 1 >> 1;
			if ( visible ( R, ( rpos + mid - 1 ) % N + 1 ) ) l = mid;
			else r = mid - 1;
		}
		int suflen = l;
		if ( prelen + suflen >= N >> 1 ) puts ( "NE" );
		else puts ( "DA" ), ++ cnt;
	}
	return 0;
}