删除其他列Table.SelectColumns（Power Query 之 M 语言）
数据源：
“姓名”“基数”“个人比例”“个人缴纳”“公司比例”“公司缴纳”“总计”，共七列
目标：
只保留“姓名”列
操作过程：
选取待保留的列》【主页】》【删除列】》【删除其他列】
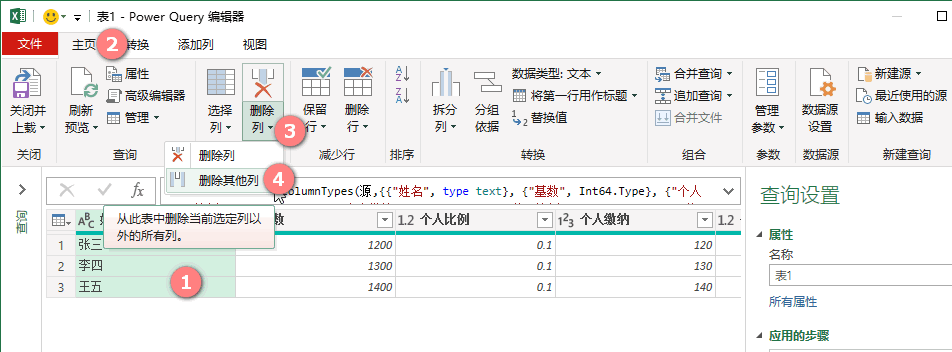
【主页】》【选择列】》取消打勾待删除的列》【确定】
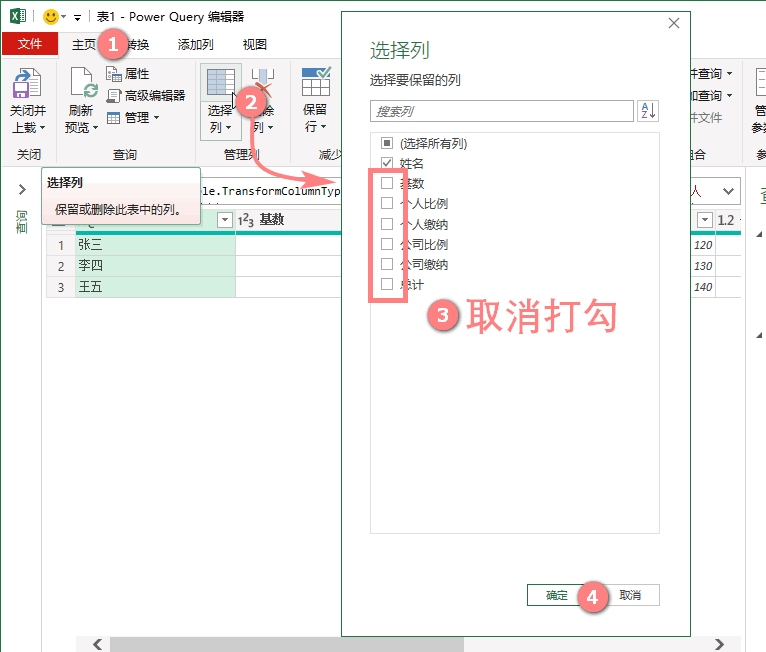
M公式：
= Table.SelectColumns( 表, {"待保留列名1",..., "待保留列名n"}, 处理不存在的列)
说明：
最终效果：
查询表只剩“姓名“列了……
多说一句：
如果不使用M公式，直接操作的话，列数多的时候，用【选择列】的方式来“咔嚓”掉不需要的列，无疑是最方便快捷的；
如果要写M公式的话，肯定是挑列数少的那种啦，七列里只删除一列用Table.RemoveColumns，只留一列用Table.SelectColumns，千万别死心眼，盯着一个函数不放，会把键盘累气虚滴~
扩展：
删除其他列Table.SelectColumns（Power Query 之 M 语言）的更多相关文章
- Table.RemoveLastN删除后面N….RemoveLastN（Power Query 之 M 语言）
数据源: "姓名""基数""个人比例""个人缴纳""公司比例""公司缴纳"&qu ...
- M函数目录（Power Query 之 M 语言）
2021-12-11更新 主页(选项卡) 管理列(组) 选择列 选择列Table.SelectColumns 删除列 删除列Table.RemoveColumns 删除其他列Table.SelectC ...
- 选择…Select…（Power Query 之 M 语言）
选择行: 筛选Table.SelectRows-文本与数值 筛选Table.SelectRows-日期与时间 保留错误行:= Table.SelectRowsWithErrors( 表, {" ...
- 删除列Table.RemoveColumns（Power Query 之 M 语言）
数据源: "姓名""基数""个人比例""个人缴纳""公司比例""公司缴纳"&qu ...
- Excel.CurrentWorkbook数据源（Power Query 之 M 语言）
数据源: 任意超级表 目标: 将超级表中的数据加载到Power Query编辑器中 操作过程: 选取超级表中任意单元格(选取普通表时会自动增加插入超级表的步骤)>数据>来自表格/区域 M公 ...
- M语言的写、改、删（Power Query 之 M 语言）
M语言基本上和其他语言一样,用敲键盘的方式写入.修改.删除,这个是废话. M语言可以在[编辑栏]或[高级编辑器]里直接写入.修改.删除,这个也是废话. M语言还有个地方可以写入.修改.删除,就是[自定 ...
- 自定义函数（Power Query 之 M 语言）
数据源: 任意工作簿 目标: 使用自定义函数实现将数据源导入Power Query编辑器 操作过程: PowerQuery编辑器>主页>新建源>其他源>空查询 编辑栏内写入公式 ...
- M语言的藏身之地（Power Query 之 M 语言）
M函数和M公式是Power Query专用的函数与公式,M代码是Power Query专用的用于实现查询功能的代码.M函数公式和M代码统称M语言. 查看M公式:[编辑栏] 查看方法:在Power Qu ...
- Table.AlternateRows删除间隔….Alternate…（Power Query 之 M 语言）
数据源: "姓名""基数""个人比例""个人缴纳""公司比例""公司缴纳"&qu ...
随机推荐
- [hdu7032]Command and Conquer: Red Alert 2
令$(x,y,z)$为狙击手的坐标,其攻击范围即以$(x,y,z)$为中心的$(2k)^{3}$的立方体 为了避免$k$的影响(二分答案会多一个$\log$),不妨将其变为以$(x,y,z)$为左下 ...
- [atAGC034F]RNG and XOR
令$N=2^{n}$先将$\forall 0\le i<N,a_{i}$除以$\sum_{i=0}^{N-1}a_{i}$,即变为概率 令$f_{i}$表示$i$的答案(第一次变成$i$的期望步 ...
- Docker极简入门：使用Docker运行Java程序
运行简单的Java程序 先在当前目录创建App.java文件 public class App{ public static void main(String[] args){ String os = ...
- 和安卓对接老是ping不通？试试内网映射
https://ngrok.cc/download.html
- [省选联考 2021 A/B 卷] 图函数
考虑到一件事情首先\(u -> u\)是可行的. 所以其实对于\(f(u,G')\) 只要考虑\([1,u]\)的点. 那么考虑其条件等价于\(u -> i\) 和 \(i -> u ...
- 【Matrix-tree Theorem学习笔记】
定义度数矩阵\(D(G)\): 定义邻接矩阵\(C(G)\): 定义\(Laplace\)矩阵\(A\) \( A(G) = D(G) - C(G) \) 记图\(G\)的所有生成树权值和为\(t(G ...
- IOI 2020 国家集训队作业
\(\checkmark\) 试题一 完成情况 试题二 完成情况 试题三 完成情况 cf549E cf674G arc103_f \(\checkmark\) cf594E agc034_f agc0 ...
- SourceTree使用图解-转
这篇文档的目的是:让使用Git更轻松. 看完这篇文档你能做到的是: 1.简单的用Git管理项目. 2.怎样既要开发又要处理发布出去的版本bug情况. SourceTree是一个免费的Git图形化管理工 ...
- 【NetCore】RabbitMQ 封装
RabbitMQ 封装 代码 https://gitee.com/wosperry/wosperry-rabbit-mqtest/tree/master 参考Abp事件总线的用法,对拷贝的Demo进行 ...
- 从零构建Java项目（Maven+SpringBoot+Git） #02 奥斯丁项目
前两天我说要写个项目来持续迭代,有好多小伙伴都表示支持和鼓励,项目的第一篇这不就来了么~我给项目取了个名字,英文名叫做:austin,中文名叫做:奥斯丁 名字倒没有什么特别的含义,我单纯觉得这个名字好 ...