北航OO第一单元作业总结(Retake)

前言：当我写这篇博客的时候，我的心情是复杂的，因为这实际上是我第二次写这篇博客——我今年重修的这门课。我对去年的成绩心有不甘——在激烈的竞争下，我虽然尽可能完成了所有作业（仅一次作业未通过弱测），但爆炸的强测分数让我最终分数很低。由于我没有进入补给站，相比于一些进补给站的同学，我没有了拯救写得稀烂的作业的机会，因此最终我的分数不如大部分补给站的同学。今年重修本次课程，我必须完成全部12次代码作业，并且要参加实验课。我不止一次动摇过，但想到这门课是最核心的专业课之一，我没有学好它，不仅仅是没有获得良好的分数，而且也表明我对于关键的工程的能力掌握得很差，我自己也清楚课程中的有些知识我掌握得并不好。最终我下定决心要学好这门课，因此选择了重修。

---

第一次作业

架构设计：　　

　　关于作业需求分析我就不过多介绍（去年已经分析过了），比去年的第一次作业仅仅增加了因子的乘法。我上学期学习了编译课程，其中语法分析部分的递归下降分析方法让我受益匪浅，我深刻体会到该方法的方便之处。因此，从第一次作业开始，我的架构就进行了谨慎的设计，我决定完全采用递归下降分析法。递归下降分析法就是为每一个待分析的非终结符编写一个子程序。由于在之后的作业中不出意外应该会加入WRONG FORMAT格式判断，可能会产生回溯问题，因此在调用分析方法时，我为了节省方法数量，让每个非终结符的判断形式（即判断WRONG FORMAT）方法以及解析方法无需分开，我设计了一个ReturnPair类，其中包含分析返回的元素以及对应源字符串的长度。内部的元素采用Object，这样就无需为所有非终结符设计一个公共子类，使用时调用instance of或getClass就可以判断元素的具体类型。如果解析失败（WRONG FORMAT），就返回null，表示调用递归子程序失败。

　　UML类图如下：

　　

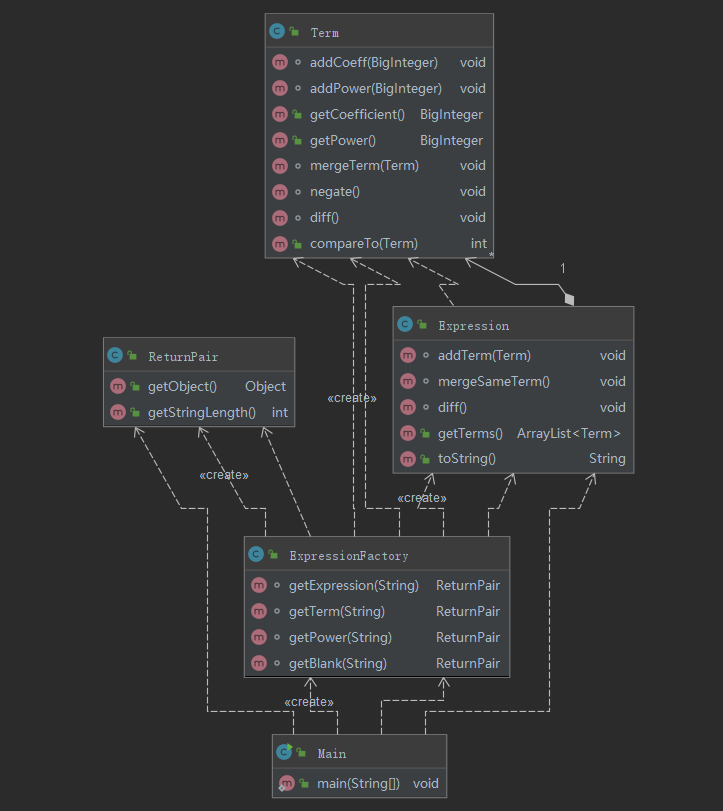
　　递归下降分析法的优点是显而易见的。我感受到的最大的优点就是调试非常方便，如果有运行不符合预期的数据，经过单步调试，很容易发现是哪个递归子程序出了问题，对其进行修改即可，不会影响到其他元素的分析。如果采用大正则的方式分析，一旦正则表达式出了差错，很容易出现找不到bug的情况。因此，我在本次作业中仅仅在最底层元素（不会调用其他元素的递归子程序）的分析中用到了正则表达式来减少工作量，并且一直沿用到第三次作业。

　　为了减小类之间的耦合程度，我在设计时采用工厂模式，将解析字符串的各级子程序放进工厂类中。由于本次因子仅包括幂函数，因此因子中仅需存储系数和指数即可包含全部信息；在求导时利用导数的加法法则逐项求导即可。

　　关于输出优化方面，实际上第一次作业的优化方式相对固定，主要就是合并同类项、系数为±1时的处理、指数为特殊情况的处理、首项符号处理等内容，可以很容易达到最优结果。

复杂度分析：

　　ev(G)意为基本复杂度。基本复杂度是用来衡量程序非结构化程度的，非结构成分降低了程序的质量，增加了代码的维护难度，使程序难于理解。因此，基本复杂度高意味着非结构化程度高，难以模块化和维护。实际上，消除了一个错误有时会引起其他的错误。iv(G)意为模块设计复杂度。模块设计复杂度是从模块流程图中移去那些不包含调用子模块的判定和循环结构后得出的圈复杂度，因此模块设计复杂度不能大于圈复杂度，通常是远小于圈复杂度。圈复杂度v(G)用来衡量一个模块判定结构的复杂程度，数量上表现为线性无关的路径条数，即合理的预防错误所需测试的最少路径条数。使用Idea的MetricsReloaded插件可以方便地分析ev(G)、iv(G)和v(G)。

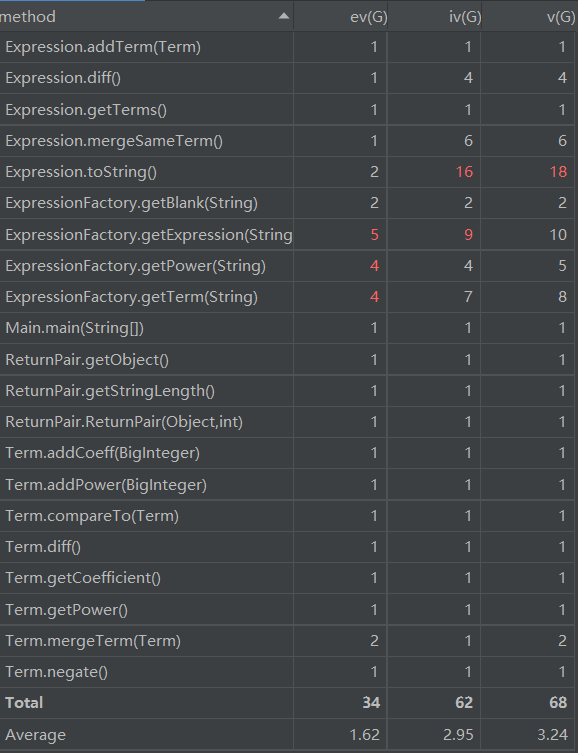
　　不管是纵向对比（与我去年的第一次作业对比）还是横向对比，我的方法整体平均复杂度都偏高。我认为可能的原因是我采用了递归下降分析法导致方法较多，同时我预留了错误处理接口。不过我认为我大多数方法的圈复杂度并没有达到需要重构的地步，我认为以略微提高复杂度为代价来采用较好的架构是值得的。

评测结果分析

　　由于我设计了评测机进行了相对充分的测试，在强测阶段我没有被测出bug。但是因为评测机数据的随机性，我并没有测出系数为-1时由于优化导致的输出格式错误，导致互测被hack。因此在设计评测机时，也要注意考虑特殊数据。同时强测中我有一些点的性能分没有拿满，由于我的强迫症，我在知道首项为正、指数为2时输出“x*x”的情况下仍然没有采用。因此我反思：没必要和分数过不去。由于可以利用评测机，因此我也发现了一些屋内其他人的bug，挽回了一些分数。

第二次作业

架构设计：

　　今年的课程第二次作业就加入了嵌套表达式以及基本的三角函数，因此我的以递归下降分析法为基础架构的就体现出了优势。和上一次作业相比，我仅仅变动了因子的设计（区分不同类型的因子），以及改变部分递归子程序的逻辑，不需要加入太多新的方法，总体来说非常方便。五种不同的因子（常数、幂函数、sin(x)、cos(x)、(表达式)）分别对应不同的求导方法。值得一提的是，对于项和表达式的存储，一开始我想采用树形结构存储，进行链式求导，但是考虑到去年部分同学遇到当表达式嵌套层数很多时因递归层数过深而导致程序超时的情况，我最终采用了ArrayList来存储并列的因子和项。对于项中连乘因子的求导，可以运用下面的公式得到（左边取对数进行求导即可得到该公式）：

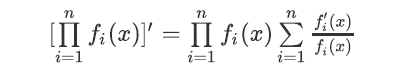
　　UML类图如下：

　　

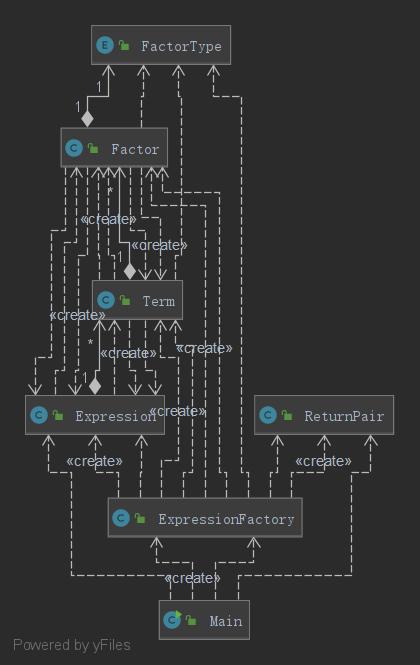
　　和上一次作业相比，这次作业我增加了FactorType这一枚举类，用于区分不同的因子类型。实际上，我曾经考虑过将不同的因子类型设计成Factor的子类，但考虑到将它们设计成子类时，这些子类并不具有独特的方法，因此这一操作就没有必要。

复杂度分析：

　　本次作业方法较多，下面给出关键方法的圈复杂度分析：

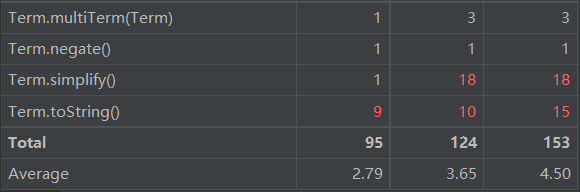
　　可以看出，复杂度较高的方法为输出以及优化方法（需要进行较多的特判）。

评测结果分析：

　　本次强测也没有被测出bug。但是没想到的是，我没有看清楚指导书里的需求，我忽视了在sin(x)和cos(x)中可能出现的空格，因为这一个bug互测被hack了十几次（大部分是被同一个人hack的）。这里要感谢课程组出的数据，如果覆盖面再广一些我可能进不了互测。

第三次作业

架构设计：

　　本次作业在上一次的基础上增加了三角函数内的表达式嵌套以及WRONG FORMAT的判断。由于之前架构的设计，我早就预留了WRONG FORMAT的接口，因此对于WRONG FORMAT的判断完全不是问题。由于三角函数支持嵌套，我在上一次作业的基础上增加了两个三角函数类：Sine和Cosine，UML类图如下：

　　

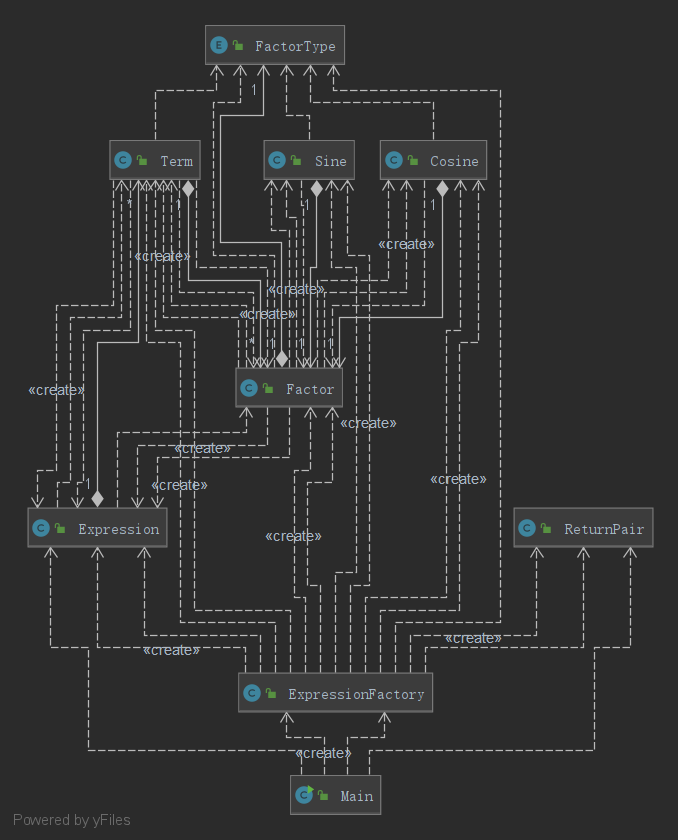
　　Sine类和Cosine类仅包含一个内部嵌套的表达式(Expression)以及自身的求导方法。值得一提的是，我为了减少求导时的时间复杂度，我在解析嵌套表达式时增加了一个简化的方法，即：如果表达式中仅含有一项，则可以在求导时去掉该层括号，这样避免了三角函数内嵌套过多时TLE。

　　主要方法的圈复杂度如图：

　　

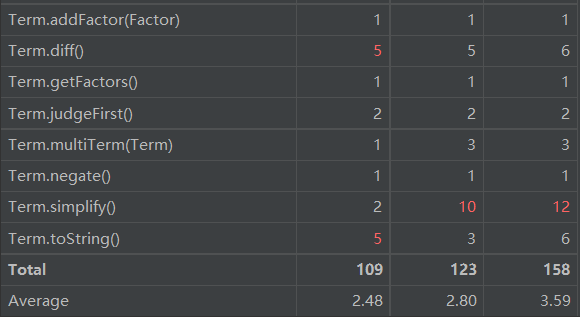
　　由于我本次作业并没有进行太多输出上的优化，因此比第二次作业的平均复杂度还要低一些。顺便提一下，我去年写的第三次作业平均ev(G)、iv(G)、v(G)分别为2.05、2.43、3.07，比今年更低，性能分也更差，因此方法过于简单有时可能意味着性能的降低。

评测结果分析：

　　强测阶段依然没有出现bug。然而在互测阶段，我又双叒叕忽略了生成规则中的空白，导致被hack。从哪里跌倒，就从哪里再跌倒一次。

总结分析

　　首先是对所有作业出现的bug进行总结。我完全没有沿用去年写的代码，全部重新设计了架构，不过我仍然没想到会出现不少bug。本单元我出现的bug全部集中在两个方面：优化时对于特殊情况的输出格式错误，以及遗漏了指导书中的某些细节。因此我认为，在拿到任务之后首先要做的应该是系统地分析需求并设计，而不是觉得“我会写”之后立马上手。同时，也不能过度依赖自动化评测，有些边缘数据还是需要自己动手测试的。出现bug的方法普遍圈复杂度以及行数都较多，但是我经过分析发现想要达到一定的性能很难将方法设计的很简单，这种问题想解决只有靠不断地测试。

　　在互测寻找其他人bug方面，我第一次作业使用了评测机以及shell脚本，发现了屋内成员的bug。但第二次作业和第三次作业我本身设计就有bug，而评测机又是根据我的设计写的，因此没有起到作用。我尝试使用一些边缘数据以及极端数据（例如大量括号嵌套）来hack，但是并没有成功。

　　关于重构的问题一直令人头疼。去年我就遇到了三次作业两次重构的情况，今年我吸取教训，在有了经验之后，第一次作业就采用容易迭代的架构，因此本单元的作业我一次都没有重构过。

　　总的来说，第二次学习本单元感觉和第一次完全不同，主要在设计理念和细节实现上具有更深的理解，到目前为止，我认为这次重修还是值得的。