【简】题解 AWSL090429 【聚会】

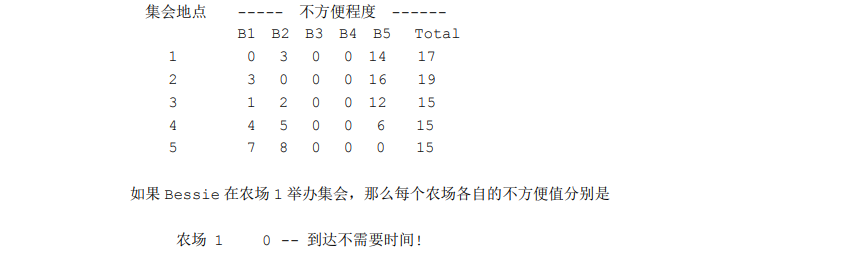
这题直接换根dp 记录在要转移的点的子树中有多少牛

#include<bits/stdc++.h>
using namespace std;
#define ll long long
#define C getchar()-48
inline ll read()
{
    ll s=0,r=1;
    char c=C;
    for(;c<0||c>9;c=C) if(c==-3) r=-1;
    for(;c>=0&&c<=9;c=C) s=(s<<3)+(s<<1)+c;
    return s*r;
}
const ll N=1e5+10,inf=1e18;
ll n,ans,mn=inf,zg;
ll c[N];
ll sz[N];
ll link[N],e[N<<1],nxt[N<<1],v[N<<1],top;
inline void llo(ll xx,ll yy,ll vv)
{
    e[++top]=yy,nxt[top]=link[xx],link[xx]=top,v[top]=vv;
}
inline void dfs(ll x,ll fa,ll deep)
{
    sz[x]=c[x];ans+=c[x]*deep;
    for(ll i=link[x];i;i=nxt[i])
    {
        ll u=e[i];
        if(u==fa) continue;
        dfs(u,x,deep+v[i]);
        sz[x]+=sz[u];
    }
}
inline void dfs2(ll x,ll fa,ll ans)
{
    mn=min(mn,ans);
    for(ll i=link[x];i;i=nxt[i])
    {
        ll u=e[i];
        if(u==fa) continue;
        dfs2(u,x,(ans+(zg-sz[u])*v[i]-(sz[u])*v[i]));
    }
}
int main()
{
    freopen("gather.in","r",stdin);
    freopen("gather.out","w",stdout);
    n=read();
    for(ll i=1;i<=n;i++) c[i]=read(),zg+=c[i];
    for(ll i=1;i<n;i++)
    {
        ll x=read(),y=read(),v=read();
        llo(x,y,v);llo(y,x,v);
    }
    dfs(1,0,0);
    dfs2(1,0,ans);
    cout<<mn;
    return 0;
}