【C/C++】two pointers/归并排序/原理/理解/实现/算法笔记4.6

1.two pointers

思路：对序列进行扫描的时候，根据序列本身的特性用两个下标i和j对序列进行扫描，从而降低算法复杂度。

·例1 在递增序列中找a + b = M

while (i<j)
   {
      if(a[i] + a[j] == M)
      {
         i++;
         j++;
      }
      else if (a[i] + a[j] < M)
      {
         i++;
      }
      else j--;
   }

·例2 序列合并问题

思路：将两个从小到大排序的序列排序出一个新的从小到大排序的序列

用两个标记i和j比较A和B中哪个小就填入哪个，剩下的多的填完。

int merge(int A[], int B[], int C[], int n, int m) //n：A长度 m：B长度 从小到大排序
{
   int i = 0, j = 0;
   int index = 0;
   while(i < n && j < m)
   {
      if (A[i] <= B[j])
      {
         C[index++] = A[i++];
      }
      else
      {
         C[index++] = B[j++];
      }
   }
   while (i < n) C[index++] = A[i++];
   while (j < m) C[index++] = B[j++];
   return index;
}

2. 归并排序

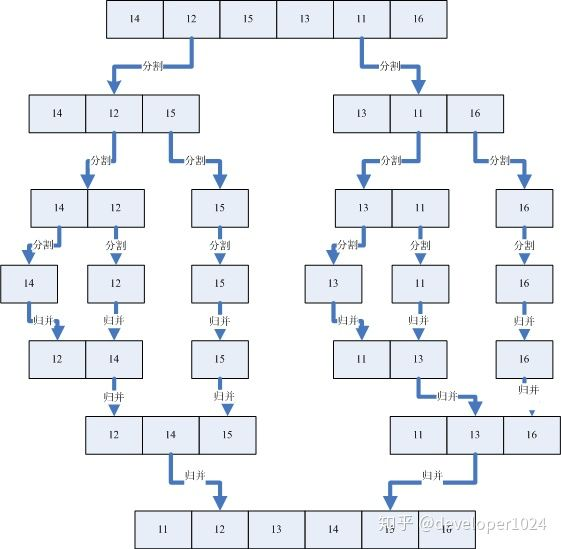
我找到一个动图特别好理解，尤其是最后分成每个是一个。

思路：2路归并排序，就是把待排序数组每次两两分组，分到每组只剩一个以后开始合并。

合并的时候遵从上面例2的方式。

因为分组是按照数组的顺序分组的，所以分组对数组的顺序其实是没有改变的。每次使用mergeSort递归只是为了获得一个更新以后的坐标，然后带入上面的序列合并的坐标位置。

真正改变的是在合并的时候

可以说这个排序是由合并本身实现的

递归边界条件是left < right，因为最后只剩一个的时候是left = right

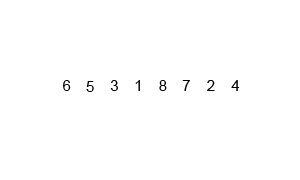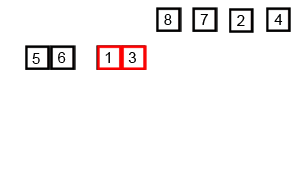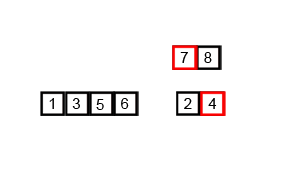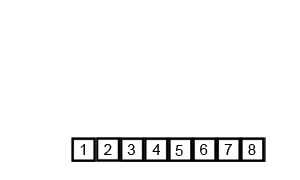
归并排序的实现：

1.递归方式

#include <iostream>
using namespace std;
const int maxn = 100;

//从小到大排序 合并函数
void merge(int A[], int L1, int R1, int L2, int R2)
{
   int temp[maxn];
   int index = 0; //记录temp的数
   int i = L1;
   int j = L2;
   while (i <= R1 && j <= R2)
   {
      if (A[i] <= A[j])
      {
         temp[index++] = A[i++];
      }
      else
      {
         temp[index++] = A[j++];
      }
   }
   while (i <= R1)
   {
      temp[index++] = A[i++];
   }
   while (j <= R2)
   {
      temp[index++] = A[j++];
   }
   for(i = 0; i < index; i++)
   {
      A[L1 + i] = temp[i];
   }
}

//分裂
void mergeSort(int A[], int left, int right)
{
   if (left < right)
   {
      int mid = (left + right)/2;
      mergeSort(A, left, mid);
      mergeSort(A, mid + 1, right);
      merge(A, left, mid, mid+1, right);  //注意这句一定要在if判断里面 这样才能退到边缘以后直接返回每一层的输出
   }
}

int main()
{
   int a[] = {6,5,3,1,8,7,2,4};
   mergeSort(a, 0, 7);
   int len = sizeof(a)/sizeof(a[0]);
   for(int i = 0; i < len; i++)
   {
      printf("%d ", a[i]);
   }
   printf("\n");
   system("pause");
}

这里我要加一些自己的理解。

测试序列：6 5 3 1 8 7 2 4

按照上述的原理，会被分成6 5；3 1；8 7；2 4；

当我们只剩下两个的时候，以6 5为例

他们分别是A[0]和A[1]

这个时候，left = 0， right = 1

计算出的mid = (left + right)/2 = 0

mid + 1 = 2

就是这个时候的left = 1 = mid, mid + 1 = 2 = right

把此时的数据带入下一步的mergeSort(A, left, mid)会因为left = right = 0而不满足mergesort中的left < right而导致无法进行下一步

这个时候就达到了递归转折退回的地方，回到了left = 0， right = 1的地方

带入merge函数，相当于执行merge(a, 0, 0, 1, 1)

其实就是排序了

以此类推

这是另外一种将mergesort和merge合并的写法

#include <stdio.h>
#include <stdlib.h>

// 归并排序（C-递归版）
void merge_sort_recursive(int arr[], int reg[], int start, int end) {
    if (start >= end)
        return;
    int len = end - start, mid = (len >> 1) + start;
    int start1 = start, end1 = mid;
    int start2 = mid + 1, end2 = end;
    merge_sort_recursive(arr, reg, start1, end1);
    merge_sort_recursive(arr, reg, start2, end2);
    int k = start;
    while (start1 <= end1 && start2 <= end2)
        reg[k++] = arr[start1] < arr[start2] ? arr[start1++] : arr[start2++];
    while (start1 <= end1)
        reg[k++] = arr[start1++];
    while (start2 <= end2)
        reg[k++] = arr[start2++];
    for (k = start; k <= end; k++)
        arr[k] = reg[k];
}
void merge_sort(int arr[], const int len) {
    int reg[len];
    merge_sort_recursive(arr, reg, 0, len - 1);
}

int main()
{
    int a[] = {6,5,3,1,8,7,2,4};
    int len = sizeof(a)/sizeof(a[0]);
    merge_sort(a, len);
    for (int i = 0; i < len; i++)
    {
        printf("%d ", a[i]);
    }
    system("pause");
}

2、非递归实现（迭代）

（注意：n = len，相同意思，指待排序的数组长度）

由二分的性质，直接对A[]进行排序（合并）

方法是：先取step = 2，然后对前step/2和后step/2进行合并排序。

如果组内元素 <= step/2，则不操作

当step/2 > n的时候结束排序

为什么不是step = n的时候结束呢？

因为如果n是奇数的话，step得多出一个（看图，每次最后一个因为不满足mid + 1 <= n而无法排序的最后一个数，在第一轮step = 2的时候就被排除在外了，多么可怜）

而要注意的是，多出一个step不能用step <= n+1来，因为step的变化是2倍变化的（step *= 2）

所以这里只能是step/2 <= n

我自己画了一个图来理解：

其实我们可以用step/2 < n就可以了:

因为如果长度为偶数的话，只需要满足 step <= n，举个栗子





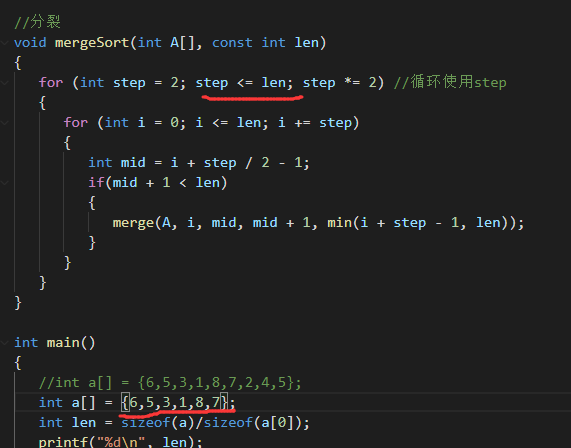
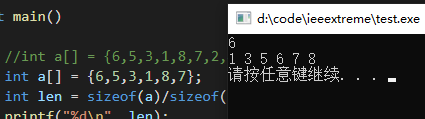
但是注意，不能是step < n，不然当数组长度刚好为step的倍数的时候最后会少一个，导致最后一个没法把两个合并。



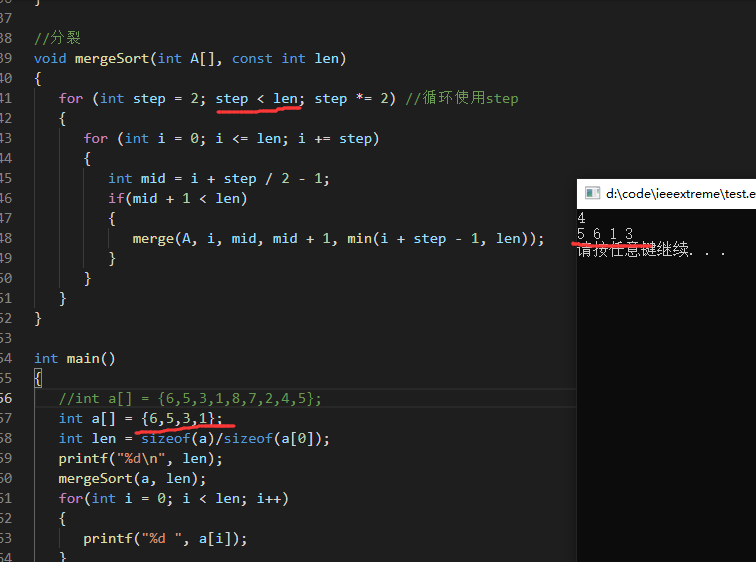
43和46行的等于好像也可以去掉，我觉得没有太大影响？