[JZOJ6088] [BZOJ5376] [loj #2463]【2018集训队互测Day 1】完美的旅行【线性递推】【多项式】【FWT】

Description

Solution

我们考虑将问题一步步拆解

第一步求出\(F_{S,i}\)表示一次旅行按位与的值为S，走了i步的方案数。

第二步答案是\(F_{S,i}\)的二维重复卷积，记答案为\(S_{S,i}\)，那么\(F_{S,i}\times S_{T,j}\)能够贡献到\(S_{S\&T,i+j}\)。

上下两部分是两个问题，我们分开来看。

考虑第一步

设原矩阵为A

根据定义，$$F_{S,i}=\sum\limits_{x&y=T}A^i_{x,y}$$

容易看出F是线性的，用题解的话来说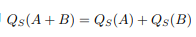，，并且内部的数乘可以移到外面

记\(f(x)\)为矩阵A的特征多项式，它是个n次多项式，根据Cayley-Hamilton定理我们有\(f(A)=0\)

可以看出F只看i这一维的话就是一个n阶线性递推。

记\(c\)就是\(x^i\)对\(f(x)\)取模的多项式系数。

我们有$$F_{S,i}=\sum\limits_{x&y=T}\sum\limits_{j=0}^{n-1}c_jA{j}_{x,y}$$

这里\(A^0\)是单位矩阵，左对角线为1，因此对于任意S，\(F_{S,0}=1\)（当然在做完以后，我们是要去掉0的，因为不允许走0步）

交换主体$$F_{S,i}=\sum\limits_{j=0}^{{n-1}c_j\sum\limits_{x&y=T}A}{j}_{x,y}$$

后面的东西就是\(F_{S,j}\)

那么就有$$F_{S,i}=\sum\limits_{j=0}^{n-1}c_jF_{S,j}$$

暴力出前n-1项的\(F\)，这是\(O(n^4)\)的

求特征多项式有很多种方法就不赘述了， 一种比较好想的做法是带入n+1个值求行列式，然后高斯消元或者拉格朗日插值求出特征多项式，这也是\(O(n^4)\)的（实际上可以\(O(n^3)\)）。

多项式取模每次只会乘一个x，直接计算最高次项的影响，时间是\(O(n)\)的

这样我们就在\(O(n^4+mn^2)\)的时间复杂度内做完了前半部分。

考虑第二步的问题：

\(F_{S,i}\)二维重复卷积，记答案为\(S_{S,i}\)，那么\(F_{S,i}\times S_{T,j}\)能够贡献到\(S_{S\&T,i+j}\)。

如果只有第二维，那很简单，直接就是\(\sum F(x)^i={1\over 1-F(x)}\)，多项式求逆就好了。

但是我们现在有了第一维

考虑将第二维固定做一遍FWT的and卷积（就是枚举第二维i，看做一个一维的集合幂\(F_i(S)\)）

那么现在所有的第一维and卷积都变成了点乘，

即原本\(F_{S\&T,i+j}+=F_{S,i}\times F_{T,j}\)

现在都变成了\(F_{S,i+j}+=F_{S,i}\times F_{S,j}\)

我们发现这时再固定第一维（枚举每个S，把\(F_S(x)\)看做一个独立的多项式），那么就变成了一维的普通幂级数重复拼接，套用多项式求逆即可。

这样我们就得到了第二维重复拼接的结果，它实际上同时进行了第一维的重复卷积。

此时按照一开始做FWT的时候固定第二维，逆FWT回去，就是最终的答案。

这一部分的复杂度是\(O(mn\log m)\)的，常数比较大。

因此我们就在\(O(mn\log m+n^4+mn^2)\)的时间复杂度解决了。

Code

（BZOJ被卡常了。。写的很丑）

#include <bits/stdc++.h>
#define fo(i,a,b) for(int i=a;i<=b;++i)
#define fod(i,a,b) for(int i=a;i>=b;--i)
#define N 20005
#define T 70
#define M 65536
#define L 16
#define LL long long
#define mo 998244353
using namespace std;
int n,m;
LL a[T][M+1],ny[M+1],c[T][T];

LL ksm(LL k,LL n)
{
	LL s=1;
	for(;n;n>>=1,k=k*k%mo) if(n&1) s=s*k%mo;
	return s;
}
//polynomial
LL ap[T][M+1],ans[T][M+1],cd[T],ct[T];
int n1;
namespace polynomial
{
	LL wi[M+1],wg[M+1];
	int bit[M+1],l2[M+1];
	void prp(int num)
	{
		fo(i,0,num)
		{
			wi[i]=wg[i*(M/num)];
			bit[i]=(bit[i>>1]>>1)|((i&1)<<(l2[num]-1));
		}
	}
	void pre()
	{
		ny[1]=1;
		fo(i,2,M) ny[i]=(-ny[mo%i]*(LL)(mo/i)%mo+mo)%mo;
		fo(i,1,L) l2[1<<i]=i;
		fod(i,M,2) if(!l2[i]) l2[i]=l2[i+1];
		wg[0]=1,wg[1]=ksm(3,(mo-1)/M);
		fo(i,2,M) wg[i]=wg[i-1]*wg[1]%mo;
	}
	void NTT(LL *a,bool pd,int num)
	{
		fo(i,0,num-1) if(i<bit[i]) swap(a[i],a[bit[i]]);
		for(int m=2,h=1,l=num>>1;m<=num;h=m,m<<=1,l>>=1)
		{
			int c=(!pd)?l:-l;
			for(int j=0;j<num;j+=m)
			{
				LL *x=a+j,*y=a+j+h,*w=(!pd)?wi:wi+num;
				fo(i,0,h-1)
				{
					LL v=*y * *w%mo;
					*y=(*x-v+mo)%mo;
					*x=(*x+v)%mo;
					x++,y++,w+=c;
				}
			}
		}
		if(pd) fo(i,0,num-1) a[i]=a[i]*ny[num]%mo;
	}
	void inv(int n,LL *a,LL *b)
	{
		static LL u1[M+1],u2[M+1];
		b[0]=ksm(a[0],mo-2);
		for(int m=1,t=2,num=4;m<n;m=t,t=num,num<<=1)
		{
			prp(num);
			fo(i,0,num-1) u1[i]=u2[i]=0;
			fo(i,0,m-1) u1[i]=b[i];
			fo(i,0,t-1)	u2[i]=a[i];
			NTT(u1,0,num),NTT(u2,0,num);
			fo(i,0,num-1) u1[i]=u1[i]*u1[i]%mo*u2[i]%mo;
			NTT(u1,1,num);
			fo(i,0,t-1) b[i]=((LL)2*b[i]-u1[i]+mo)%mo;
			fo(i,t,num-1) b[i]=0;
		}
	}
	void gmod()
	{
		LL v=ksm(cd[n1],mo-2)*ct[n1]%mo;
		fo(i,0,n1) ct[i]=(ct[i]-v*cd[i]%mo+mo)%mo;
	}
}

using namespace polynomial;

//matrix
LL c1[T][T],al[T][T];

namespace matrix
{
	void ti()
	{
		static LL z[T][T];
		memset(z,0,sizeof(z));
		fo(i,0,n-1)
		{
			fo(k,0,n-1)
			{
				fo(j,0,n-1) z[i][j]=(z[i][j]+c1[i][k]*c[k][j])%mo;
			}
		}
		fo(i,0,n-1) fo(j,0,n-1) c1[i][j]=z[i][j];
	}

	LL det(int k)
	{
		static LL z[T][T];
		memcpy(z,c,sizeof(c));
		fo(i,0,n-1) z[i][i]=(z[i][i]-k+mo)%mo;
		LL v=1;
		fo(i,0,n-1)
		{
			fo(k,i,n-1)
			{
				if(z[k][i])
				{
					if(k!=i) swap(z[k],z[i]),v=-v;
					break;
				}
			}
			if(!z[i][i]) return 0;
			LL vn=ksm(z[i][i],mo-2);
			fo(k,i+1,n-1)
			{
				if(z[k][i])
				{
					LL v=z[k][i]*vn%mo;
					fo(j,i,n-1) z[k][j]=(z[k][j]-v*z[i][j])%mo;
				}
			}
		}
		fo(i,0,n-1) v=v*z[i][i]%mo;
		return v;
	}
	void gauss()
	{
		fo(i,0,n)
		{
			fo(k,i,n)
			{
				if(al[k][i])
				{
					if(k!=i) swap(al[k],al[i]);
					break;
				}
			}
			if(!al[i][i]) continue;
			LL v=ksm(al[i][i],mo-2)%mo;
			fo(k,i,n+1) al[i][k]=al[i][k]*v%mo;
			fo(k,i+1,n)
			{
				if(al[k][i])
				{
					v=al[k][i];
					fo(j,i,n+1) al[k][j]=(al[k][j]-v*al[i][j])%mo;
				}
			}
		}
		fod(i,n,0)
		{
			if(al[i][i])
			{
				fod(k,i-1,0)
				{
					if(al[k][i])
					{
						LL v=al[k][i];
						fo(j,i,n+1) al[k][j]=(al[k][j]-v*al[i][j])%mo;
					}
				}
			}
		}
	}
}
using namespace matrix;

void FWT(int t,bool pd)
{
	for(int m=2,h=1;m<=n;h=m,m<<=1)
		for(int j=0;j<n;j+=m)
			fo(i,0,h-1) a[i+j][t]=(a[i+j][t]+((!pd)?1:-1)*a[i+j+h][t]+mo)%mo;
}

int main()
{
	cin>>n>>m;
	pre();
	fo(i,0,n-1)
		fo(j,0,n-1)
			scanf("%lld\n",&c[i][j]),c1[i][j]=c[i][j];

	fo(i,0,n)
	{
		LL v=i;
		al[i][0]=1;
		fo(j,1,n) al[i][j]=v,v=v*(LL)i%mo;
		al[i][n+1]=det(i);
	}

	gauss();

	fo(i,0,n) cd[i]=al[i][n+1];
	n1=n;
	fo(i,0,n-1) a[i][0]=1;
	while(cd[n1]==0) n1--;
	fo(i,1,n1-1)
	{
		fo(x,0,n1-1) fo(y,0,n-1) a[x&y][i]=(a[x&y][i]+c1[x][y])%mo;
		ti();
	}
	ct[n1-1]=1;
	fo(i,n1,m)
	{
		fod(j,n1,1) ct[j]=ct[j-1];
		ct[0]=0;
		gmod();
		fo(x,0,n-1) fo(j,0,n1-1) a[x][i]=(a[x][i]+ct[j]*a[x][j]%mo+mo)%mo;
	} 

	fo(i,0,n-1) a[i][0]=0;
	memset(ap,0,sizeof(ap));
	fo(j,1,m) FWT(j,0);
	fo(i,0,n-1)
	{
		a[i][0]++;
		fo(j,1,m) a[i][j]=-a[i][j];
		inv(m+1,a[i],ap[i]);
	}

	fo(j,1,m)
	{
		fo(i,0,n-1) a[i][j]=ap[i][j];
		FWT(j,1);
	}

	LL ans=0;
	fo(i,0,n-1) fo(j,1,m) ans^=a[i][j];
	printf("%lld\n",ans);
}