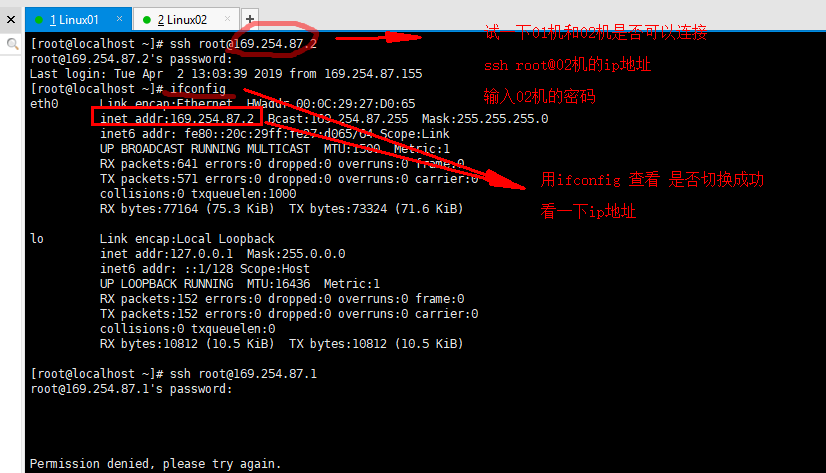
先试一下 01机和02机是否可以切换成功

使用 ssh root@ip地址

输入密码

ifconfig查看ip是否正确

切换回01机

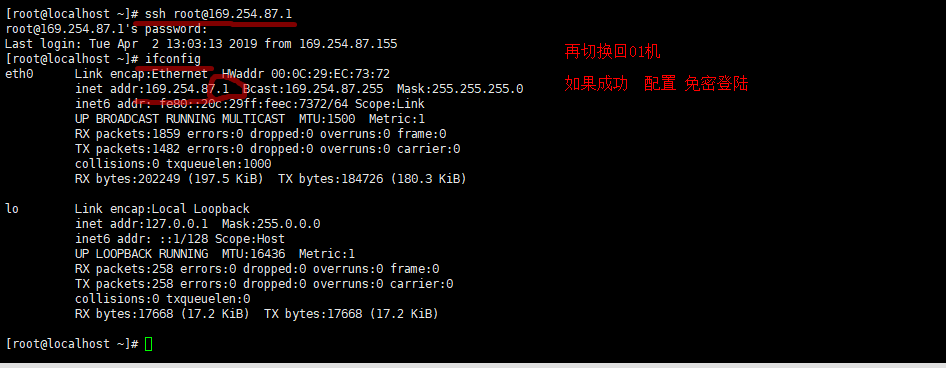
01机配置的秘钥

查看隐形文件

01机配置秘钥

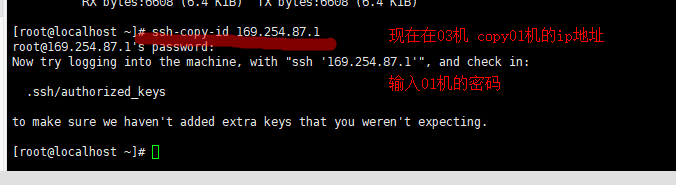
输入  ssh-copy-id   02机的ip地址

输入  ssh-copy-id   03机的ip地址

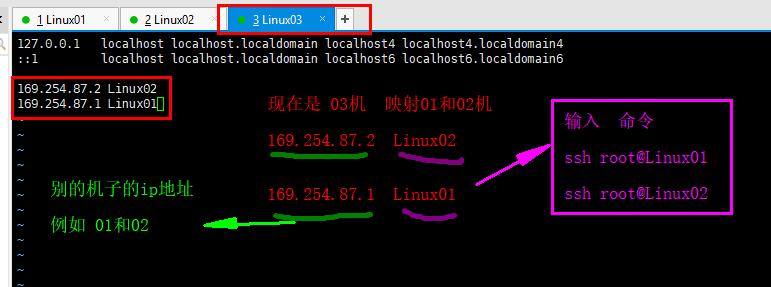
输入 vim /etc/hosts  命令

进入编辑

作为一个真正的程序员，首先应该尊重编程，热爱你所写下的程序，他是你的伙伴，而不是工具。

Linux01机和Linux02机的切换 和秘钥的配置的更多相关文章

  1. 解决方案-问题001：物理机、虚机等等Linux操作系统/usr/bin目录权限误操作,导致无法切换root

    导语:平常运维人员会误操作一些目录权限,导致一些问题,那么如何恢复呢? 问题:物理机.虚机等等Linux操作系统/usr/bin目录权限误操作,导致无法切换root? 实验环境: ip地址 是否目录正 ...

  2. ansible 安装 使用 命令 笔记 生成密钥 管控机 被管控机 wget epel源

      ansible 与salt对比 相同 都是为了同时在多台机器上执行相同的命令 都是python开发 不同 agent(saltstack需要安装.ansible不需要) 配置(salt配置麻烦,a ...

  3. ansible Ansible Galaxy ansible-playbook 安装 使用 命令 笔记 生成密钥 管控机 被管控机 wget epel源

    笔记 ansible 安装 与salt对比 相同 都是为了同时在多台机器上执行相同的命令 都是python开发 不同 agent(saltstack需要安装.ansible不需要) 配置(salt配置 ...

  4. 获取本机 Android 默认sha1 秘钥

    获取本机 Android 默认sha1 秘钥: 以Windows操作系统为例,打开CMD,运行以下指令将得到所有默认秘钥. keytool -list -v -keystore C:\Users\pa ...

  5. 我的小前端 （1）—— 安卓机和ios机的区别

    没有什么特别新技术,就是记录我做移动端遇到的问题 2016-02-16 微信,支付宝和APP都会遇到这些问题 一.安卓机和ios机的区别 1.常用 <head>        <me ...

  6. 01_Weblogic课程之概念篇：代理服务器，web服务器，应用程序服务器，JNDI概念，JTA概念，Java消息服务，Java验证和授权（JAAS）,Java管理扩展，Web客户机，客户机应用程序

     1 什么是服务器 Weblogic中服务器分为两种,一种是受管服务器,另外一种是管理服务器. Weblogic课程(Weblogic是Oracle公司的,最开始的是BEA公司的) 一 系统管理 ...

  7. Openstack中用秘钥对(keypair)生成和访问虚机的方法

    Openstack中用镜像文件生成的image来创建虚机(VM或Instance)时, 通常不支持用户名加密码的ssh方式登录访问该VM,而是用秘钥对(keypair)方式. 这里以Centos的镜像 ...

  8. SAP客户端 测试机、开发机、生产机

     SAP客户端 测试机.开发机.生产机     客户端(即Client),是SAP组织架构里最高层的组织单元,所有数据,包括静态数据(科目.客户.供应商.物料.资产等).业务数据(采购订单.销售订单. ...

  9. 如何配置 Oracle VirtualBox 中的客户机与物理机网络

    当你在 Oracle VirtualBox 虚拟机软件 中安装了各种操作系统时,你可能需要实现物理机与虚拟机之间的相互访问. 在这篇文章中,我们将会以最简单明了的方式来说明如何配置客户机与 Linux ...

随机推荐

  1. vue事件双向绑定

    事件 案例: vue的事件绑定原理:改变图片的背景颜色问题来实现这个框架的使用方法, new Vue({ el:"", data:{}, methord:{}, computed: ...

  2. AB实验的高端玩法系列3 - AB组不随机？观测试验？Propensity Score

    背景 都说随机是AB实验的核心,为什么随机这么重要呢?有人说因为随机所以AB组整体不存在差异,这样才能准确估计实验效果(ATE) \[ ATE = E(Y_t(1) - Y_c(0)) \] 那究竟随 ...

  3. 前端技术之：如何在控制台将JS class实例输出为JSON格式

    有一个类: class Point { constructor(x, y) { this.x = x; this.y = y; } } 如果我们在控制台中输出其实例: console.log(new ...

  4. lua程序设计（一）

    摘要:lua程序设计第二版学习笔记 脚本语言的基础语法大都比较简单,这里只列举一些lua独有,或者需要特别注意的语法点. 书中前三章的内容是一些惯常的引言,基础数据类型,运算符等内容,相对简单,这里就 ...

  5. 有关logistic(sigmoid)函数回归

    在神经网络中,经常用到sigmoid函数,y = 1 / (1+e-x) 作为下一级神经元的激活函数,x也就是WX(下文,W以θ符号代替)矩阵计算结果. 这个函数通常用在进行分类,通常分为1或0的逻辑 ...

  6. 微服务SpringCloud之GateWay服务化和过滤器

    Spring Cloud Gateway 提供了一种默认转发的能力,只要将 Spring Cloud Gateway 注册到服务中心,Spring Cloud Gateway 默认就会代理服务中心的所 ...

  7. CSP-S 46 题解

    改完题了,就稍写一下题解,顺便反思一下! 其实这次考试挺水的,然而我也挺水的,看了考试结束后的成绩,就吃-*了! T1 set 这个我考试的时候实在是没有想到如何去判断-1,然后我就觉得这神仙题没法解 ...

  8. 易初大数据 2019年11月13日 Linux 王庆超

    ★安装Red Hat Enterprise Linux7.41 ◆1通过键盘的方向键选择“lnstall Red Hat Enterprise Linux7.4”选项来直接安装Linux 系统. ◆2 ...

  9. servlet三大组件

    servlet大致可以分为三个:简单servlet.过滤servlet.监听servlet servlet: servlet的创建 创建一个类并实现Servlet接口. 重写service方法. 在服 ...

  10. java笔试面试第一天

    好久未曾启用我的博客,最近来上海找工作,想将笔试面试的过程做个记录,毕竟有总结才有提高嘛.今天算是笔试面试正式开始第一天吧,以下就是我的笔试总结(没有原题了,只有知识点): 笔试题1:java sta ...