postgresql12 b-tree v4空间上和性能上的优化

在 pg v11 和 v12 上 常见测试用例

CREATE TABLE rel (
a bigint NOT NULL,
b bigint NOT NULL
);

ALTER TABLE rel
ADD CONSTRAINT rel_pkey PRIMARY KEY (a, b);

CREATE INDEX rel_b_idx ON rel (b);

\d rel
Table "public.rel"
Column | Type | Collation | Nullable | Default
--------+--------+-----------+----------+---------
a | bigint | | not null |
b | bigint | | not null |
Indexes:
"rel_pkey" PRIMARY KEY, btree (a, b)
"rel_b_idx" btree (b)

• 它确保“a”和“b” 两字段的每种组合最多有一个条目。
• 它可以加快与给定“b”相关的所有“a”的搜索速度。

加入测试数据

INSERT INTO rel (a, b)
   SELECT i, i / 10000
   FROM generate_series(1, 20000000) AS i;

/* 收集统计信息 */
VACUUM (ANALYZE) rel;

B-tree索引提高1：插入很多重复的索引和数值
当我们比较的b列索引的大小的第一个区别是显而易见的：

v11:
\di+ rel_b_idx
                           List of relations
 Schema |    Name     | Type  |  Owner   | Table |  Size  | Description
--------+-------------+-------+----------+-------+--------+-------------
 public | rel_b_idx | index | postgres | rel   | 545 MB |
(1 row)
v12:
\di+ rel_b_idx

 Schema |    Name     | Type  |  Owner   | Table |  Size  | Description
--------+-------------+-------+----------+-------+--------+-------------
 public | rel_b_idx | index | postgres | rel   | 408 MB |
(1 row)

v11 比 v12 还要大 33%

每一个b列在index发生10000次，因此会有很多叶子节点的所有密钥是相同的（每个叶子节点可以包含几百项）。

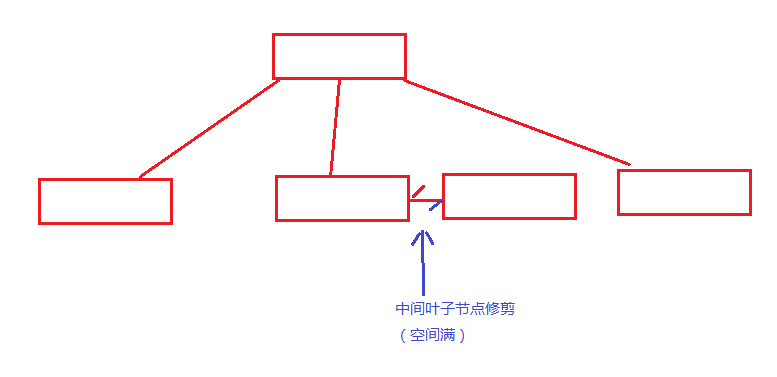
V12之前，叶子页必须是分立的，有时是最右边的叶子节点，但有时不是。最右边的叶子节点总是朝着右端，

以优化单调递增插入拆分。与此相反，其他叶子节点是在中间，其中浪费的空间分割。

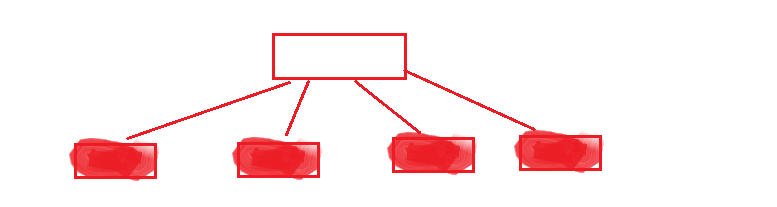
与V12，该表的行的物理地址（“元组ID”或TID）是索引关键字的一部分，所以重复的索引条目存储在表的顺序。

这会造成这样的条目索引扫描访问的物理顺序表，它可以是一个显著的性能优势，特别是在机械磁盘。

换句话说，重复索引条目的相关性将是完美的。而且，仅由重复的页将在右端分裂，产生密集索引。

加入类似的优化多列索引，但它并不适用于我们的主键索引，因为重复不是在第1列。

主键索引在V11和V12紧凑，因为第一列是单调递增的，所以叶页拆分在最右边的页面总是发生。

PostgreSQL的已经有针对的优化。

B-tree索引提高2：内部索引页面的压缩存储

对于主键索引的改进是不那么明显，因为它们几乎在尺寸在V11和V12相同。我们必须更深入的挖掘这里。

首先，观察指标，只有在这两个V11和V12（块缓存）扫描：

在v11:
EXPLAIN (ANALYZE, BUFFERS, COSTS off, SUMMARY off, TIMING off)
S
SELECT a, b FROM rel
W
WHERE a = 420024 AND b = 42;

                          QUERY PLAN
-
---------------------------------------------------------------

 Index Only Scan using rel_pkey on rel (actual rows=1 loops=1)

   Index Cond: ((a = 420024) AND (b = 42))

   Heap Fetches: 0

   Buffers: shared hit=5
(
(4 rows)

在v12:
EXPLAIN (ANALYZE, BUFFERS, COSTS off, SUMMARY off, TIMING off)
S
SELECT a, b FROM rel
W
WHERE a = 420024 AND b = 42;

                          QUERY PLAN
-
---------------------------------------------------------------

 Index Only Scan using rel_pkey on rel (actual rows=1 loops=1)

   Index Cond: ((a = 420024) AND (b = 42))

   Heap Fetches: 0

   Buffers: shared hit=4
(
(4 rows)

在v12中，将读取少一（索引）的块，这意味着该索引少一级。
由于索引的大小几乎相同，因此必须意味着内部页面可以容纳更多的索引条目。
在v12中，索引具有更大的扇出度。

如上所述，PostgreSQL的V12引入的TID作为索引关键字，这会浪费在内部索引页的空间过多量的一部分。

所以同一个commit引入的来自内部 Page “冗余”索引属性。该TID是多余的，

因为是从包含子句非键属性（V11这些也从内部索引页除去）。

不过，PostgreSQL的V12也可以截断不需要的表行识别这些指标的属性。

在我们的主键索引，出价是一个冗余列，并从内部索引页，

从而节省了8个字节的每个索引条目空间。让我们一起来看看与pageinspect扩展内部索引页：

在 v11:
SELECT * FROM bt_page_items('rel_pkey', 2550);

 itemoffset |    ctid    | itemlen | nulls | vars |                      data
-
------------+------------+---------+-------+------+-------------------------------------------------

          1 | (2667,88)  |      24 | f     | f    | cd 8f 0a 00 00 00 00 00 45 00 00 00 00 00 00 00

          2 | (2462,0)   |       8 | f     | f    | 

          3 | (2463,15)  |      24 | f     | f    | d6 c0 09 00 00 00 00 00 3f 00 00 00 00 00 00 00

          4 | (2464,91)  |      24 | f     | f    | db c1 09 00 00 00 00 00 3f 00 00 00 00 00 00 00

          5 | (2465,167) |      24 | f     | f    | e0 c2 09 00 00 00 00 00 3f 00 00 00 00 00 00 00

          6 | (2466,58)  |      24 | f     | f    | e5 c3 09 00 00 00 00 00 3f 00 00 00 00 00 00 00

          7 | (2467,134) |      24 | f     | f    | ea c4 09 00 00 00 00 00 40 00 00 00 00 00 00 00

          8 | (2468,25)  |      24 | f     | f    | ef c5 09 00 00 00 00 00 40 00 00 00 00 00 00 00

          9 | (2469,101) |      24 | f     | f    | f4 c6 09 00 00 00 00 00 40 00 00 00 00 00 00 00

         10 | (2470,177) |      24 | f     | f    | f9 c7 09 00 00 00 00 00 40 00 00 00 00 00 00 00
.
...

        205 | (2666,12)  |      24 | f     | f    | c8 8e 0a 00 00 00 00 00 45 00 00 00 00 00 00 00
(
(205 rows)

在数据输入我们所看到的援助和出价字节。该实验在 little-endian 机器上进行的，
所以在第6行的数目将是0x09C3E5和0x3F的或（十进制数）639973和63.每个索引条目是24个字节宽，这8个字节是所述元组报头。

在 v12:
SELECT * FROM bt_page_items('rel_pkey', 2700);

 itemoffset |   ctid   | itemlen | nulls | vars |          data
-
------------+----------+---------+-------+------+-------------------------

          1 | (2862,1) |      16 | f     | f    | ab 59 0b 00 00 00 00 00

          2 | (2576,0) |       8 | f     | f    | 

          3 | (2577,1) |      16 | f     | f    | 1f 38 0a 00 00 00 00 00

          4 | (2578,1) |      16 | f     | f    | 24 39 0a 00 00 00 00 00

          5 | (2579,1) |      16 | f     | f    | 29 3a 0a 00 00 00 00 00

          6 | (2580,1) |      16 | f     | f    | 2e 3b 0a 00 00 00 00 00

          7 | (2581,1) |      16 | f     | f    | 33 3c 0a 00 00 00 00 00

          8 | (2582,1) |      16 | f     | f    | 38 3d 0a 00 00 00 00 00

          9 | (2583,1) |      16 | f     | f    | 3d 3e 0a 00 00 00 00 00

         10 | (2584,1) |      16 | f     | f    | 42 3f 0a 00 00 00 00 00
.
...

        286 | (2861,1) |      16 | f     | f    | a6 58 0b 00 00 00 00 00
(
(286 rows)

该数据仅包含a列，因为a列已经被截断了。这减少了索引项的大小为16，让更多的条目适合索引页上。

升级注意事项
由于索引存储在V12被改变，新的B-tree索引第4版已经推出。

由于与pg_upgrade不改变数据文件升级，索引仍然会在3.0版本升级后。
PostgreSQL的V12可以使用这些指标，但上述的优化将不可用。
你需要重新索引的索引将其升级到4.0版本（这已经在PostgreSQL的V12变得更加容易与REINDEX兼）。

其他B-tree索引功能在推出V12
有PostgreSQL中V12添加了一些其他方面的改进。如下简单列表：

1. 减少B树索引插入，以提高性能锁定开销。
2. REINDEX CONCURRENTLY，重建无停机时间的索引。
3. 完善与许多属性的索引仅索引扫描性能。
4. 添加视图 pg_stat_progress_create_index 报到CREATE INDEX和REINDEX进展。

补充一下btree version4代码

/*
 * lib/btree.c    - Simple In-memory B+Tree
 *
 * As should be obvious for Linux kernel code, license is GPLv2
 *
 * Copyright (c) 2007-2008 Joern Engel <joern@purestorage.com>
 * Bits and pieces stolen from Peter Zijlstra's code, which is
 * Copyright 2007, Red Hat Inc. Peter Zijlstra
 * GPLv2
 *
 * see http://programming.kicks-ass.net/kernel-patches/vma_lookup/btree.patch
 *
 * A relatively simple B+Tree implementation.  I have written it as a learning
 * exercise to understand how B+Trees work.  Turned out to be useful as well.
 *
 * B+Trees can be used similar to Linux radix trees (which don't have anything
 * in common with textbook radix trees, beware).  Prerequisite for them working
 * well is that access to a random tree node is much faster than a large number
 * of operations within each node.
 *
 * Disks have fulfilled the prerequisite for a long time.  More recently DRAM
 * has gained similar properties, as memory access times, when measured in cpu
 * cycles, have increased.  Cacheline sizes have increased as well, which also
 * helps B+Trees.
 *
 * Compared to radix trees, B+Trees are more efficient when dealing with a
 * sparsely populated address space.  Between 25% and 50% of the memory is
 * occupied with valid pointers.  When densely populated, radix trees contain
 * ~98% pointers - hard to beat.  Very sparse radix trees contain only ~2%
 * pointers.
 *
 * This particular implementation stores pointers identified by a long value.
 * Storing NULL pointers is illegal, lookup will return NULL when no entry
 * was found.
 *
 * A tricks was used that is not commonly found in textbooks.  The lowest
 * values are to the right, not to the left.  All used slots within a node
 * are on the left, all unused slots contain NUL values.  Most operations
 * simply loop once over all slots and terminate on the first NUL.
 */

#include <linux/btree.h>
#include <linux/cache.h>
#include <linux/kernel.h>
#include <linux/slab.h>
#include <linux/module.h>

#define MAX(a, b) ((a) > (b) ? (a) : (b))
#define NODESIZE MAX(L1_CACHE_BYTES, 128)

struct btree_geo {
    int keylen;
    int no_pairs;
    int no_longs;
};

struct btree_geo btree_geo32 = {
    .keylen = ,
    .no_pairs = NODESIZE / sizeof(long) / ,
    .no_longs = NODESIZE / sizeof(long) / ,
};
EXPORT_SYMBOL_GPL(btree_geo32);

#define LONG_PER_U64 (64 / BITS_PER_LONG)
struct btree_geo btree_geo64 = {
    .keylen = LONG_PER_U64,
    .no_pairs = NODESIZE / sizeof(long) / ( + LONG_PER_U64),
    .no_longs = LONG_PER_U64 * (NODESIZE / sizeof(long) / ( + LONG_PER_U64)),
};
EXPORT_SYMBOL_GPL(btree_geo64);

struct btree_geo btree_geo128 = {
    .keylen =  * LONG_PER_U64,
    .no_pairs = NODESIZE / sizeof(long) / ( +  * LONG_PER_U64),
    .no_longs =  * LONG_PER_U64 * (NODESIZE / sizeof(long) / ( +  * LONG_PER_U64)),
};
EXPORT_SYMBOL_GPL(btree_geo128);

#define MAX_KEYLEN    (2 * LONG_PER_U64)

static struct kmem_cache *btree_cachep;

void *btree_alloc(gfp_t gfp_mask, void *pool_data)
{
    return kmem_cache_alloc(btree_cachep, gfp_mask);
}
EXPORT_SYMBOL_GPL(btree_alloc);

void btree_free(void *element, void *pool_data)
{
    kmem_cache_free(btree_cachep, element);
}
EXPORT_SYMBOL_GPL(btree_free);

static unsigned long *btree_node_alloc(struct btree_head *head, gfp_t gfp)
{
    unsigned long *node;

    node = mempool_alloc(head->mempool, gfp);
    if (likely(node))
        memset(node, , NODESIZE);
    return node;
}

static int longcmp(const unsigned long *l1, const unsigned long *l2, size_t n)
{
    size_t i;

    for (i = ; i < n; i++) {
        if (l1[i] < l2[i])
            return -;
        if (l1[i] > l2[i])
            return ;
    }
    return ;
}

static unsigned long *longcpy(unsigned long *dest, const unsigned long *src,
        size_t n)
{
    size_t i;

    for (i = ; i < n; i++)
        dest[i] = src[i];
    return dest;
}

static unsigned long *longset(unsigned long *s, unsigned long c, size_t n)
{
    size_t i;

    for (i = ; i < n; i++)
        s[i] = c;
    return s;
}

static void dec_key(struct btree_geo *geo, unsigned long *key)
{
    unsigned long val;
    int i;

    for (i = geo->keylen - ; i >= ; i--) {
        val = key[i];
        key[i] = val - ;
        if (val)
            break;
    }
}

static unsigned long *bkey(struct btree_geo *geo, unsigned long *node, int n)
{
    return &node[n * geo->keylen];
}

static void *bval(struct btree_geo *geo, unsigned long *node, int n)
{
    return (void *)node[geo->no_longs + n];
}

static void setkey(struct btree_geo *geo, unsigned long *node, int n,
           unsigned long *key)
{
    longcpy(bkey(geo, node, n), key, geo->keylen);
}

static void setval(struct btree_geo *geo, unsigned long *node, int n,
           void *val)
{
    node[geo->no_longs + n] = (unsigned long) val;
}

static void clearpair(struct btree_geo *geo, unsigned long *node, int n)
{
    longset(bkey(geo, node, n), , geo->keylen);
    node[geo->no_longs + n] = ;
}

static inline void __btree_init(struct btree_head *head)
{
    head->node = NULL;
    head->height = ;
}

void btree_init_mempool(struct btree_head *head, mempool_t *mempool)
{
    __btree_init(head);
    head->mempool = mempool;
}
EXPORT_SYMBOL_GPL(btree_init_mempool);

int btree_init(struct btree_head *head)
{
    __btree_init(head);
    head->mempool = mempool_create(, btree_alloc, btree_free, NULL);
    if (!head->mempool)
        return -ENOMEM;
    return ;
}
EXPORT_SYMBOL_GPL(btree_init);

void btree_destroy(struct btree_head *head)
{
    mempool_free(head->node, head->mempool);
    mempool_destroy(head->mempool);
    head->mempool = NULL;
}
EXPORT_SYMBOL_GPL(btree_destroy);

void *btree_last(struct btree_head *head, struct btree_geo *geo,
         unsigned long *key)
{
    int height = head->height;
    unsigned long *node = head->node;

    if (height == )
        return NULL;

    for ( ; height > ; height--)
        node = bval(geo, node, );

    longcpy(key, bkey(geo, node, ), geo->keylen);
    return bval(geo, node, );
}
EXPORT_SYMBOL_GPL(btree_last);

static int keycmp(struct btree_geo *geo, unsigned long *node, int pos,
          unsigned long *key)
{
    return longcmp(bkey(geo, node, pos), key, geo->keylen);
}

static int keyzero(struct btree_geo *geo, unsigned long *key)
{
    int i;

    for (i = ; i < geo->keylen; i++)
        if (key[i])
            return ;

    return ;
}

void *btree_lookup(struct btree_head *head, struct btree_geo *geo,
        unsigned long *key)
{
    int i, height = head->height;
    unsigned long *node = head->node;

    if (height == )
        return NULL;

    for ( ; height > ; height--) {
        for (i = ; i < geo->no_pairs; i++)
            if (keycmp(geo, node, i, key) <= )
                break;
        if (i == geo->no_pairs)
            return NULL;
        node = bval(geo, node, i);
        if (!node)
            return NULL;
    }

    if (!node)
        return NULL;

    for (i = ; i < geo->no_pairs; i++)
        if (keycmp(geo, node, i, key) == )
            return bval(geo, node, i);
    return NULL;
}
EXPORT_SYMBOL_GPL(btree_lookup);

int btree_update(struct btree_head *head, struct btree_geo *geo,
         unsigned long *key, void *val)
{
    int i, height = head->height;
    unsigned long *node = head->node;

    if (height == )
        return -ENOENT;

    for ( ; height > ; height--) {
        for (i = ; i < geo->no_pairs; i++)
            if (keycmp(geo, node, i, key) <= )
                break;
        if (i == geo->no_pairs)
            return -ENOENT;
        node = bval(geo, node, i);
        if (!node)
            return -ENOENT;
    }

    if (!node)
        return -ENOENT;

    for (i = ; i < geo->no_pairs; i++)
        if (keycmp(geo, node, i, key) == ) {
            setval(geo, node, i, val);
            return ;
        }
    return -ENOENT;
}
EXPORT_SYMBOL_GPL(btree_update);

/*
 * Usually this function is quite similar to normal lookup.  But the key of
 * a parent node may be smaller than the smallest key of all its siblings.
 * In such a case we cannot just return NULL, as we have only proven that no
 * key smaller than __key, but larger than this parent key exists.
 * So we set __key to the parent key and retry.  We have to use the smallest
 * such parent key, which is the last parent key we encountered.
 */
void *btree_get_prev(struct btree_head *head, struct btree_geo *geo,
             unsigned long *__key)
{
    int i, height;
    unsigned long *node, *oldnode;
    unsigned long *retry_key = NULL, key[MAX_KEYLEN];

    if (keyzero(geo, __key))
        return NULL;

    if (head->height == )
        return NULL;
    longcpy(key, __key, geo->keylen);
retry:
    dec_key(geo, key);

    node = head->node;
    for (height = head->height ; height > ; height--) {
        for (i = ; i < geo->no_pairs; i++)
            if (keycmp(geo, node, i, key) <= )
                break;
        if (i == geo->no_pairs)
            goto miss;
        oldnode = node;
        node = bval(geo, node, i);
        if (!node)
            goto miss;
        retry_key = bkey(geo, oldnode, i);
    }

    if (!node)
        goto miss;

    for (i = ; i < geo->no_pairs; i++) {
        if (keycmp(geo, node, i, key) <= ) {
            if (bval(geo, node, i)) {
                longcpy(__key, bkey(geo, node, i), geo->keylen);
                return bval(geo, node, i);
            } else
                goto miss;
        }
    }
miss:
    if (retry_key) {
        longcpy(key, retry_key, geo->keylen);
        retry_key = NULL;
        goto retry;
    }
    return NULL;
}
EXPORT_SYMBOL_GPL(btree_get_prev);

static int getpos(struct btree_geo *geo, unsigned long *node,
        unsigned long *key)
{
    int i;

    for (i = ; i < geo->no_pairs; i++) {
        if (keycmp(geo, node, i, key) <= )
            break;
    }
    return i;
}

static int getfill(struct btree_geo *geo, unsigned long *node, int start)
{
    int i;

    for (i = start; i < geo->no_pairs; i++)
        if (!bval(geo, node, i))
            break;
    return i;
}

/*
 * locate the correct leaf node in the btree
 */
static unsigned long *find_level(struct btree_head *head, struct btree_geo *geo,
        unsigned long *key, int level)
{
    unsigned long *node = head->node;
    int i, height;

    for (height = head->height; height > level; height--) {
        for (i = ; i < geo->no_pairs; i++)
            if (keycmp(geo, node, i, key) <= )
                break;

        if ((i == geo->no_pairs) || !bval(geo, node, i)) {
            /* right-most key is too large, update it */
            /* FIXME: If the right-most key on higher levels is
             * always zero, this wouldn't be necessary. */
            i--;
            setkey(geo, node, i, key);
        }
        BUG_ON(i < );
        node = bval(geo, node, i);
    }
    BUG_ON(!node);
    return node;
}

static int btree_grow(struct btree_head *head, struct btree_geo *geo,
              gfp_t gfp)
{
    unsigned long *node;
    int fill;

    node = btree_node_alloc(head, gfp);
    if (!node)
        return -ENOMEM;
    if (head->node) {
        fill = getfill(geo, head->node, );
        setkey(geo, node, , bkey(geo, head->node, fill - ));
        setval(geo, node, , head->node);
    }
    head->node = node;
    head->height++;
    return ;
}

static void btree_shrink(struct btree_head *head, struct btree_geo *geo)
{
    unsigned long *node;
    int fill;

    if (head->height <= )
        return;

    node = head->node;
    fill = getfill(geo, node, );
    BUG_ON(fill > );
    head->node = bval(geo, node, );
    head->height--;
    mempool_free(node, head->mempool);
}

static int btree_insert_level(struct btree_head *head, struct btree_geo *geo,
                  unsigned long *key, void *val, int level,
                  gfp_t gfp)
{
    unsigned long *node;
    int i, pos, fill, err;

    BUG_ON(!val);
    if (head->height < level) {
        err = btree_grow(head, geo, gfp);
        if (err)
            return err;
    }

retry:
    node = find_level(head, geo, key, level);
    pos = getpos(geo, node, key);
    fill = getfill(geo, node, pos);
    /* two identical keys are not allowed */
    BUG_ON(pos < fill && keycmp(geo, node, pos, key) == );

    if (fill == geo->no_pairs) {
        /* need to split node */
        unsigned long *new;

        new = btree_node_alloc(head, gfp);
        if (!new)
            return -ENOMEM;
        err = btree_insert_level(head, geo,
                bkey(geo, node, fill /  - ),
                new, level + , gfp);
        if (err) {
            mempool_free(new, head->mempool);
            return err;
        }
        for (i = ; i < fill / ; i++) {
            setkey(geo, new, i, bkey(geo, node, i));
            setval(geo, new, i, bval(geo, node, i));
            setkey(geo, node, i, bkey(geo, node, i + fill / ));
            setval(geo, node, i, bval(geo, node, i + fill / ));
            clearpair(geo, node, i + fill / );
        }
        if (fill & ) {
            setkey(geo, node, i, bkey(geo, node, fill - ));
            setval(geo, node, i, bval(geo, node, fill - ));
            clearpair(geo, node, fill - );
        }
        goto retry;
    }
    BUG_ON(fill >= geo->no_pairs);

    /* shift and insert */
    for (i = fill; i > pos; i--) {
        setkey(geo, node, i, bkey(geo, node, i - ));
        setval(geo, node, i, bval(geo, node, i - ));
    }
    setkey(geo, node, pos, key);
    setval(geo, node, pos, val);

    return ;
}

int btree_insert(struct btree_head *head, struct btree_geo *geo,
        unsigned long *key, void *val, gfp_t gfp)
{
    BUG_ON(!val);
    return btree_insert_level(head, geo, key, val, , gfp);
}
EXPORT_SYMBOL_GPL(btree_insert);

static void *btree_remove_level(struct btree_head *head, struct btree_geo *geo,
        unsigned long *key, int level);
static void merge(struct btree_head *head, struct btree_geo *geo, int level,
        unsigned long *left, int lfill,
        unsigned long *right, int rfill,
        unsigned long *parent, int lpos)
{
    int i;

    for (i = ; i < rfill; i++) {
        /* Move all keys to the left */
        setkey(geo, left, lfill + i, bkey(geo, right, i));
        setval(geo, left, lfill + i, bval(geo, right, i));
    }
    /* Exchange left and right child in parent */
    setval(geo, parent, lpos, right);
    setval(geo, parent, lpos + , left);
    /* Remove left (formerly right) child from parent */
    btree_remove_level(head, geo, bkey(geo, parent, lpos), level + );
    mempool_free(right, head->mempool);
}

static void rebalance(struct btree_head *head, struct btree_geo *geo,
        unsigned long *key, int level, unsigned long *child, int fill)
{
    unsigned long *parent, *left = NULL, *right = NULL;
    int i, no_left, no_right;

    if (fill == ) {
        /* Because we don't steal entries from a neighbour, this case
         * can happen.  Parent node contains a single child, this
         * node, so merging with a sibling never happens.
         */
        btree_remove_level(head, geo, key, level + );
        mempool_free(child, head->mempool);
        return;
    }

    parent = find_level(head, geo, key, level + );
    i = getpos(geo, parent, key);
    BUG_ON(bval(geo, parent, i) != child);

    if (i > ) {
        left = bval(geo, parent, i - );
        no_left = getfill(geo, left, );
        if (fill + no_left <= geo->no_pairs) {
            merge(head, geo, level,
                    left, no_left,
                    child, fill,
                    parent, i - );
            return;
        }
    }
    if (i +  < getfill(geo, parent, i)) {
        right = bval(geo, parent, i + );
        no_right = getfill(geo, right, );
        if (fill + no_right <= geo->no_pairs) {
            merge(head, geo, level,
                    child, fill,
                    right, no_right,
                    parent, i);
            return;
        }
    }
    /*
     * We could also try to steal one entry from the left or right
     * neighbor.  By not doing so we changed the invariant from
     * "all nodes are at least half full" to "no two neighboring
     * nodes can be merged".  Which means that the average fill of
     * all nodes is still half or better.
     */
}

static void *btree_remove_level(struct btree_head *head, struct btree_geo *geo,
        unsigned long *key, int level)
{
    unsigned long *node;
    int i, pos, fill;
    void *ret;

    if (level > head->height) {
        /* we recursed all the way up */
        head->height = ;
        head->node = NULL;
        return NULL;
    }

    node = find_level(head, geo, key, level);
    pos = getpos(geo, node, key);
    fill = getfill(geo, node, pos);
    if ((level == ) && (keycmp(geo, node, pos, key) != ))
        return NULL;
    ret = bval(geo, node, pos);

    /* remove and shift */
    for (i = pos; i < fill - ; i++) {
        setkey(geo, node, i, bkey(geo, node, i + ));
        setval(geo, node, i, bval(geo, node, i + ));
    }
    clearpair(geo, node, fill - );

    if (fill -  < geo->no_pairs / ) {
        if (level < head->height)
            rebalance(head, geo, key, level, node, fill - );
        else if (fill -  == )
            btree_shrink(head, geo);
    }

    return ret;
}

void *btree_remove(struct btree_head *head, struct btree_geo *geo,
        unsigned long *key)
{
    if (head->height == )
        return NULL;

    return btree_remove_level(head, geo, key, );
}
EXPORT_SYMBOL_GPL(btree_remove);

int btree_merge(struct btree_head *target, struct btree_head *victim,
        struct btree_geo *geo, gfp_t gfp)
{
    unsigned long key[MAX_KEYLEN];
    unsigned long dup[MAX_KEYLEN];
    void *val;
    int err;

    BUG_ON(target == victim);

    if (!(target->node)) {
        /* target is empty, just copy fields over */
        target->node = victim->node;
        target->height = victim->height;
        __btree_init(victim);
        return ;
    }

    /* TODO: This needs some optimizations.  Currently we do three tree
     * walks to remove a single object from the victim.
     */
    for (;;) {
        if (!btree_last(victim, geo, key))
            break;
        val = btree_lookup(victim, geo, key);
        err = btree_insert(target, geo, key, val, gfp);
        if (err)
            return err;
        /* We must make a copy of the key, as the original will get
         * mangled inside btree_remove. */
        longcpy(dup, key, geo->keylen);
        btree_remove(victim, geo, dup);
    }
    return ;
}
EXPORT_SYMBOL_GPL(btree_merge);

static size_t __btree_for_each(struct btree_head *head, struct btree_geo *geo,
                   unsigned long *node, unsigned long opaque,
                   void (*func)(void *elem, unsigned long opaque,
                        unsigned long *key, size_t index,
                        void *func2),
                   void *func2, int reap, int height, size_t count)
{
    int i;
    unsigned long *child;

    for (i = ; i < geo->no_pairs; i++) {
        child = bval(geo, node, i);
        if (!child)
            break;
        if (height > )
            count = __btree_for_each(head, geo, child, opaque,
                    func, func2, reap, height - , count);
        else
            func(child, opaque, bkey(geo, node, i), count++,
                    func2);
    }
    if (reap)
        mempool_free(node, head->mempool);
    return count;
}

static void empty(void *elem, unsigned long opaque, unsigned long *key,
          size_t index, void *func2)
{
}

void visitorl(void *elem, unsigned long opaque, unsigned long *key,
          size_t index, void *__func)
{
    visitorl_t func = __func;

    func(elem, opaque, *key, index);
}
EXPORT_SYMBOL_GPL(visitorl);

void visitor32(void *elem, unsigned long opaque, unsigned long *__key,
           size_t index, void *__func)
{
    visitor32_t func = __func;
    u32 *key = (void *)__key;

    func(elem, opaque, *key, index);
}
EXPORT_SYMBOL_GPL(visitor32);

void visitor64(void *elem, unsigned long opaque, unsigned long *__key,
           size_t index, void *__func)
{
    visitor64_t func = __func;
    u64 *key = (void *)__key;

    func(elem, opaque, *key, index);
}
EXPORT_SYMBOL_GPL(visitor64);

void visitor128(void *elem, unsigned long opaque, unsigned long *__key,
        size_t index, void *__func)
{
    visitor128_t func = __func;
    u64 *key = (void *)__key;

    func(elem, opaque, key[], key[], index);
}
EXPORT_SYMBOL_GPL(visitor128);

size_t btree_visitor(struct btree_head *head, struct btree_geo *geo,
             unsigned long opaque,
             void (*func)(void *elem, unsigned long opaque,
                       unsigned long *key,
                       size_t index, void *func2),
             void *func2)
{
    size_t count = ;

    if (!func2)
        func = empty;
    if (head->node)
        count = __btree_for_each(head, geo, head->node, opaque, func,
                func2, , head->height, );
    return count;
}
EXPORT_SYMBOL_GPL(btree_visitor);

size_t btree_grim_visitor(struct btree_head *head, struct btree_geo *geo,
              unsigned long opaque,
              void (*func)(void *elem, unsigned long opaque,
                       unsigned long *key,
                       size_t index, void *func2),
              void *func2)
{
    size_t count = ;

    if (!func2)
        func = empty;
    if (head->node)
        count = __btree_for_each(head, geo, head->node, opaque, func,
                func2, , head->height, );
    __btree_init(head);
    return count;
}
EXPORT_SYMBOL_GPL(btree_grim_visitor);

static int __init btree_module_init(void)
{
    btree_cachep = kmem_cache_create("btree_node", NODESIZE, ,
            SLAB_HWCACHE_ALIGN, NULL);
    return ;
}

static void __exit btree_module_exit(void)
{
    kmem_cache_destroy(btree_cachep);
}

/* If core code starts using btree, initialization should happen even earlier */
module_init(btree_module_init);
module_exit(btree_module_exit);

MODULE_AUTHOR("Joern Engel <joern@logfs.org>");
MODULE_AUTHOR("Johannes Berg <johannes@sipsolutions.net>");
MODULE_LICENSE("GPL");

总结

拥有许多重复的条目索引, V12 更有优势 , 推荐 pg_upgrade后用 REINDEX CONCURRENTLY 重新索引。