AutoCAD中的螺旋究竟是什么螺旋？

AutoCad从很早的时候就开始提供了螺旋线的功能，它的用法相对简单，非常适合用来对等距螺旋的理论进行演练。

选择螺旋线工具，首先画出一个基准圆，再向内（或向外）移动鼠标，拖出一个旋转3个周期的螺旋。

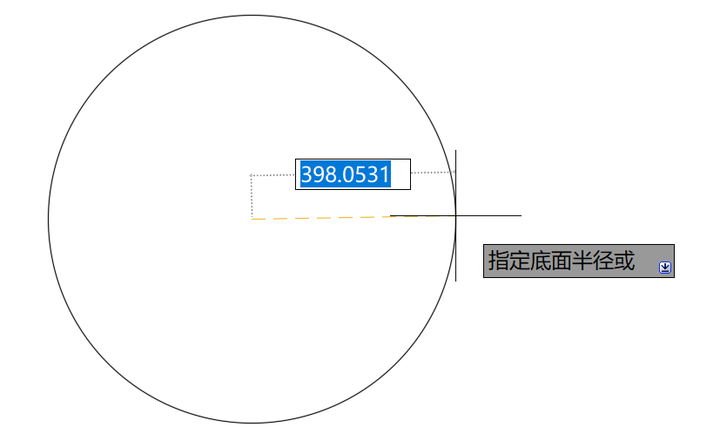
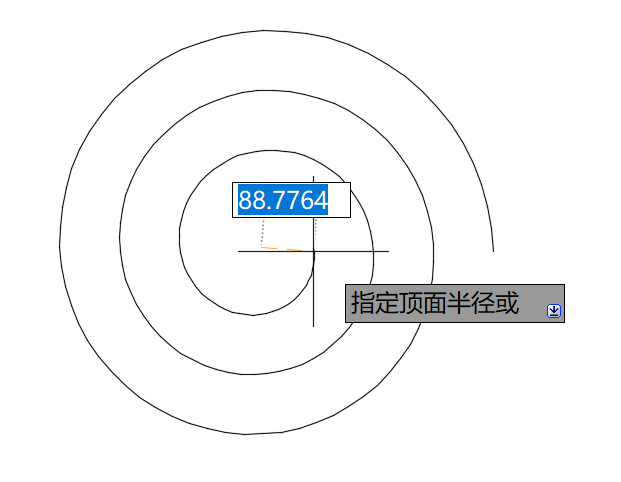
Autocad中把螺旋的起点称作底面半径，结束点称为顶面半径（这里的螺旋功能是可以画三维螺旋的）。拖动底面半径的起点时，螺旋整体会变化。拖动顶面半径时，底面半径是固定不变的。因此，在使用时，应尽量先指定好底面半径，之后调整顶面半径来控制螺旋的大小。

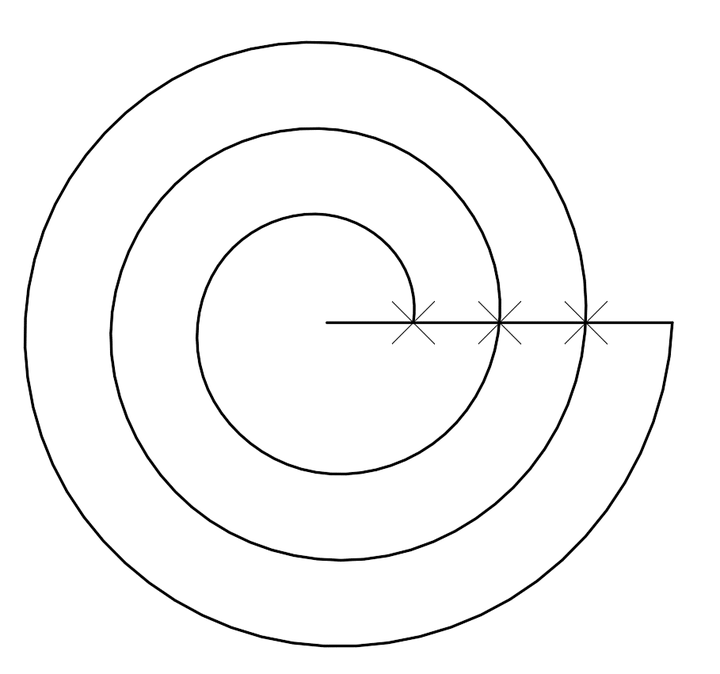
从螺旋的特征来看，在这三个旋转周期中，每一个周期，螺旋外扩相同的距离，因此，它属于典型的等距螺旋。

按照等距螺旋的理论，螺旋是由直线运动与圆周运动的叠加而产生的轨迹。若直线运动与圆周运动的速度之比是固定值，则会产生等距离外扩的螺旋，因此，把这一类的螺旋称为等距（离外扩）螺旋，也可以称为等速度比螺旋。

根据直线与圆周的位置关系及速度比的变化，等距螺旋分为以下几种主要的类别。

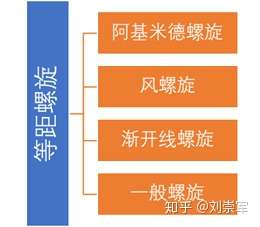等距螺旋的分类

直线过圆心，速度比恒定时，会产生阿基米德螺旋。速度比为1，直线与圆周相切，运动方向相反时，会产生渐开线螺旋。【速度比】等于【直线距圆心的距离】与【圆周半径】的比值时，会产生风螺旋。其它的速度比与直线位置没有直接关系的螺旋，早些时候，我称它们为自由螺旋，但是“自由”这个两字已经被香港青年们玩坏了，所以，改称为一般螺旋好了。

理论铺垫了这么多，还没开始我们的问题，CAD中的螺旋研究是什么螺旋？怎么证明呢？

一点点来看，我们先画一个底边半径为60，每个旋转周期外扩20的螺旋，顶面半径为60+3*20=120的螺旋，如下图所示：

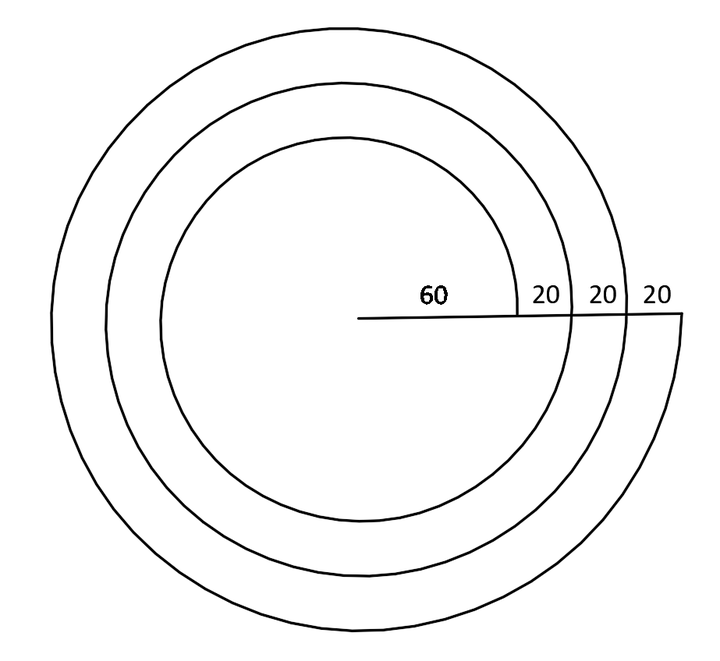
从这张图进行判断，螺旋如果继续向内收缩，再经过3个螺旋周期，它必将通过圆心。所以我们可以直接画一个从圆心开始，每周期外扩20的螺旋，可以得到下面的红色部分的螺旋（具体绘制步骤：先画底边半径60，再指向圆心，令顶面半径为0）：

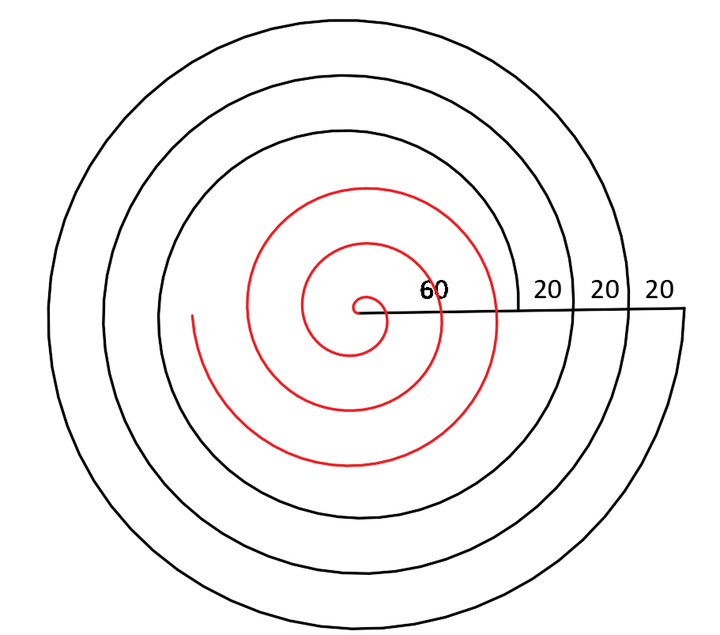
理论上说红色螺旋与黑色螺旋采用了相同的参数，从位置关系上看，它们之间相差了180度。将红色螺旋旋转180度，再上下镜像一下，见证奇迹的时间到了，它们是一致的，并且是标准的阿基米德螺旋。

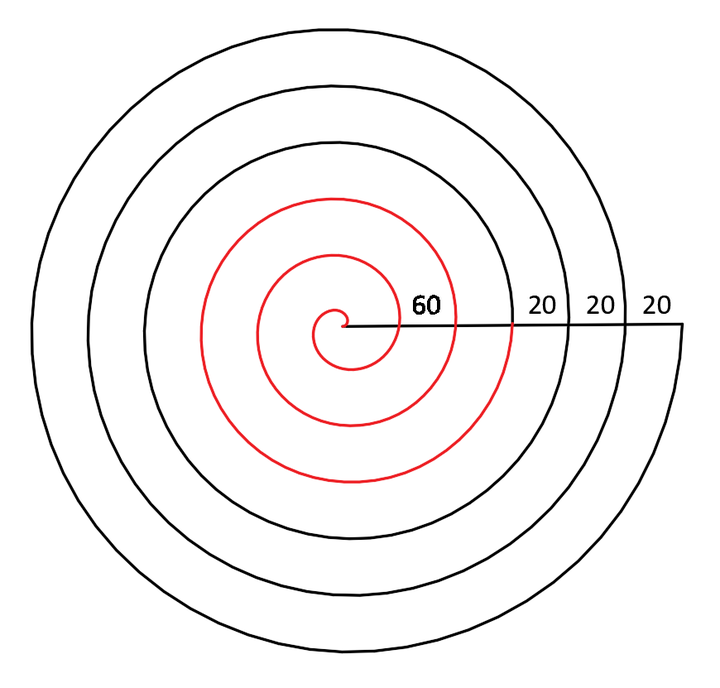
上面的螺旋是按照数据计算得到的结果，螺旋通过圆心是符合预期的结果。那么如果将底面半径设计为100，顶面半径为10，3个旋转周期中每周期收缩30，螺旋将会是下面的样子，这样的螺旋是否还会通过圆心呢？

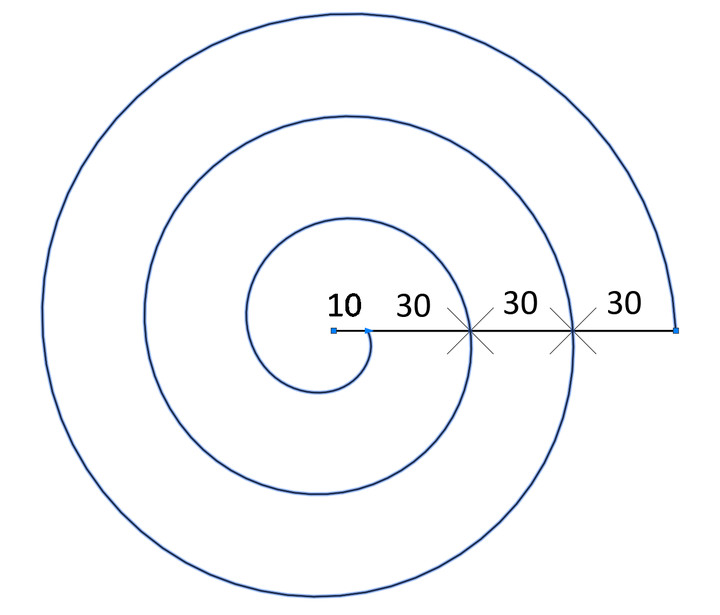
若按照30距离单位收缩，可以预见，下一回合完成后，螺旋会进入到外扩的过程中，并且可以通过距离圆心20单位的位置点。我们直接从这个20距离点开始画螺旋，外扩30，3个周期，顶面半径为20+3*30=110。得到下面的效果。

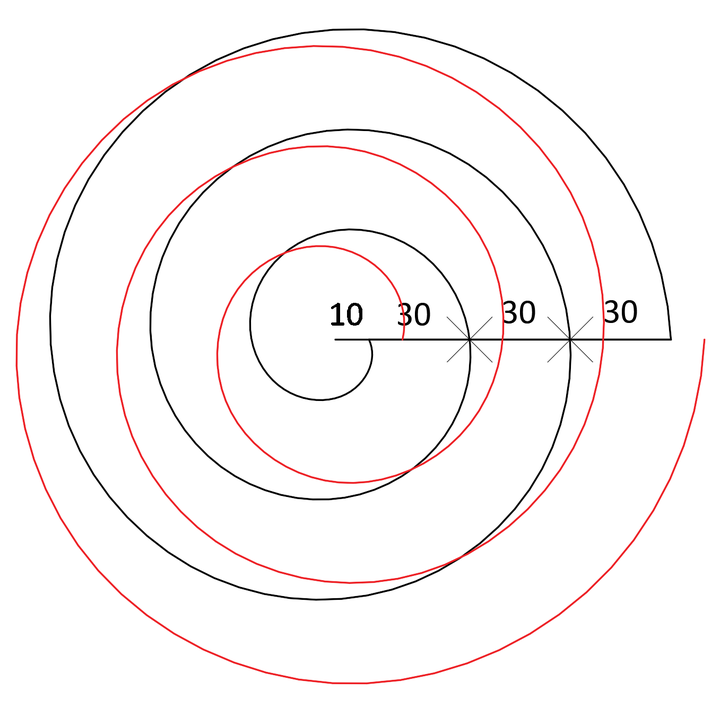
根据等距螺旋的理论，完整的螺旋是轴对称图形，可以找到一条过圆心的直线，将螺旋的外扩部分与内收部分对称起来。上图中红色螺旋与黑色螺旋的交点位于同一条线上，可以按照我们所了解的对称性，进行一下验证。

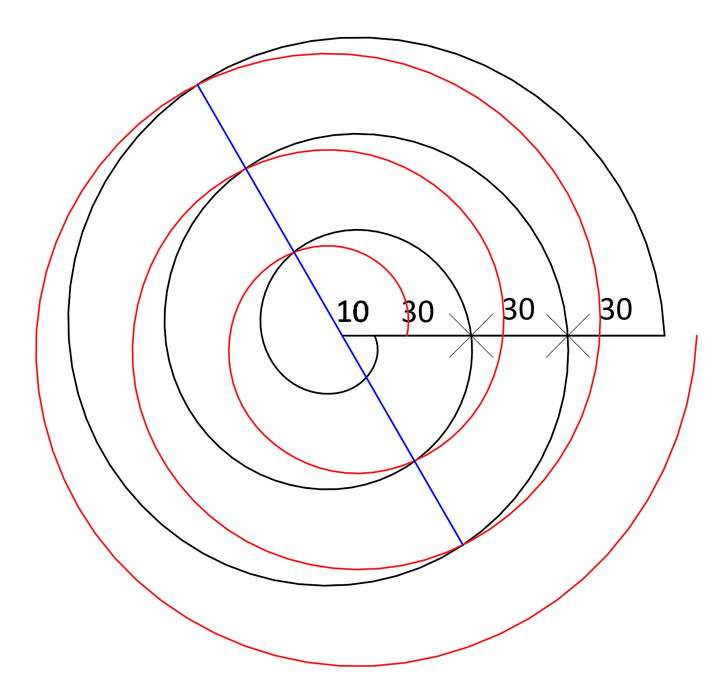
如果螺旋画得够准的话，连接螺旋线的交点得到的对称轴会通过圆心，如上图中的蓝色线条所示。通过对称轴将黑色螺旋进行镜像，得到的镜像部分会将红色螺旋完全覆盖，即两部分螺旋会重合，如下图所示。

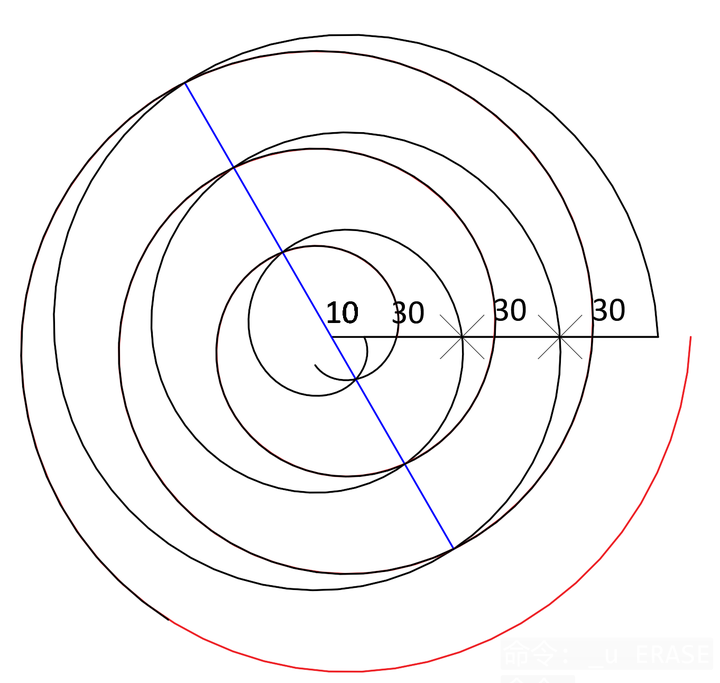
通过以上的操作，可以发现计算关系相同的两条件螺旋可以是镜像关系，但作为螺旋运动来说，它们是怎样通过圆心并且进行连接的呢？

我们可以按照阿基米德螺旋的方式，沿水平向右方向来画一条底面半径为90，顶面半径为0的螺旋，来比较一下。（下图中删除掉了镜像得到的黑色螺旋）

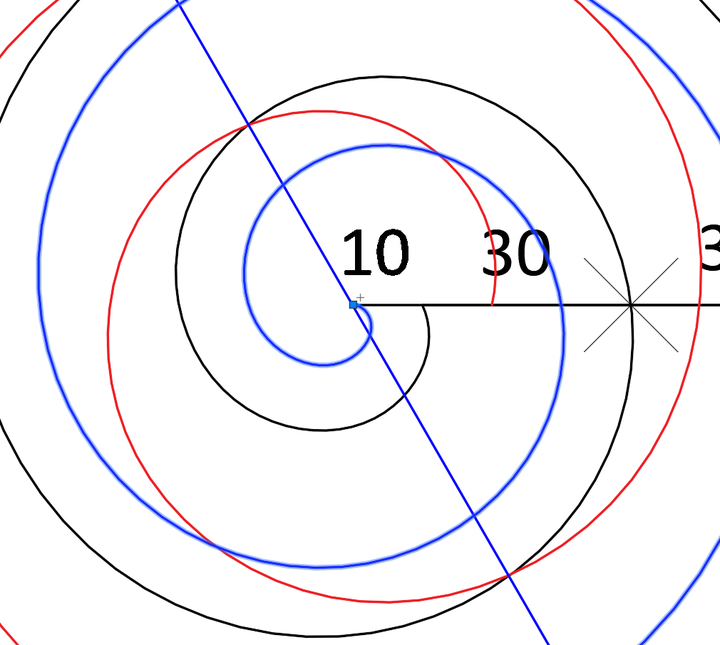
我们相信蓝色螺旋与另外两个螺旋是相同的，只是初始方向不一样，通过旋转蓝色螺旋必然会与黑色螺旋重合。

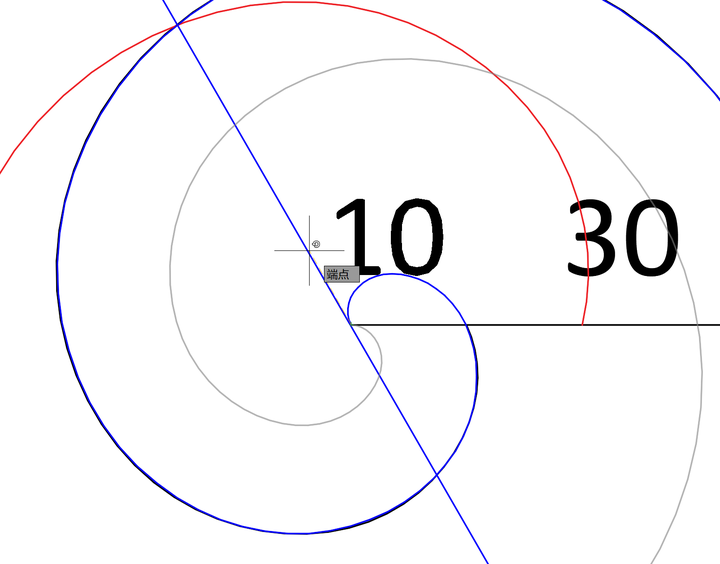
旋转时会发现，当旋转至对称轴时，蓝色螺旋会与黑色螺旋重合。对称轴再一次发挥了作用，而这个不是巧合，是必然。我们已经知道黑色螺旋与红色螺旋沿对称轴互为镜像，所以只需将蓝色螺旋进行镜像可得到穿过圆心的红色螺旋。

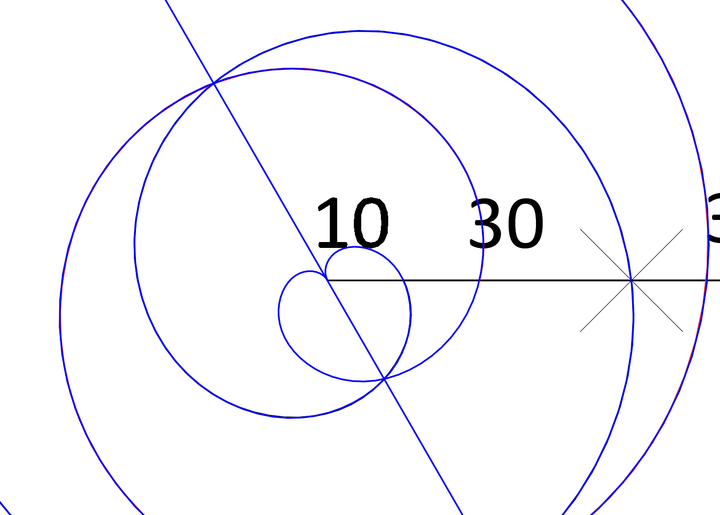
上图中两条蓝色螺旋虽然通过了圆心，但并未实现平滑连接的效果，这不符合我们关于螺旋运动是平滑而连续的特性。

它们实际上是离开圆心之后，出门左转，与出门右转的关系，这是阿基米德螺旋所特有的对称特性。也就是说前面绘制的黑色螺旋与红色螺旋，它们分别位于左转和右转 两个方向的螺旋之上，这两个螺旋沿对称轴对称。

再来分析一下，对称轴可以看作是阿基米德螺旋初始运动的方向，那么它必然也是螺旋在圆心位置的切线，我们沿对称轴过圆心画一条绿色垂线，如下图所示。

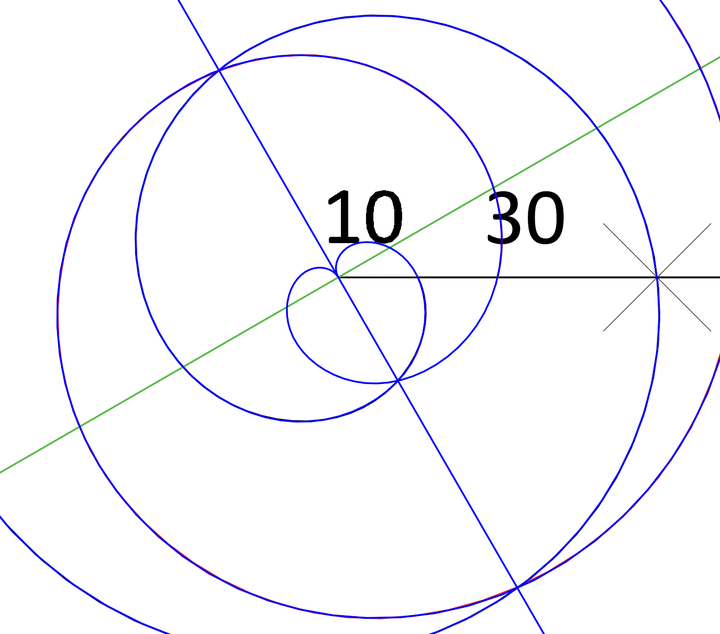
沿对称轴的垂线，对螺旋做镜像（或者逆时针螺旋旋转180度），可以得到平滑衔接的阿基米德螺旋。

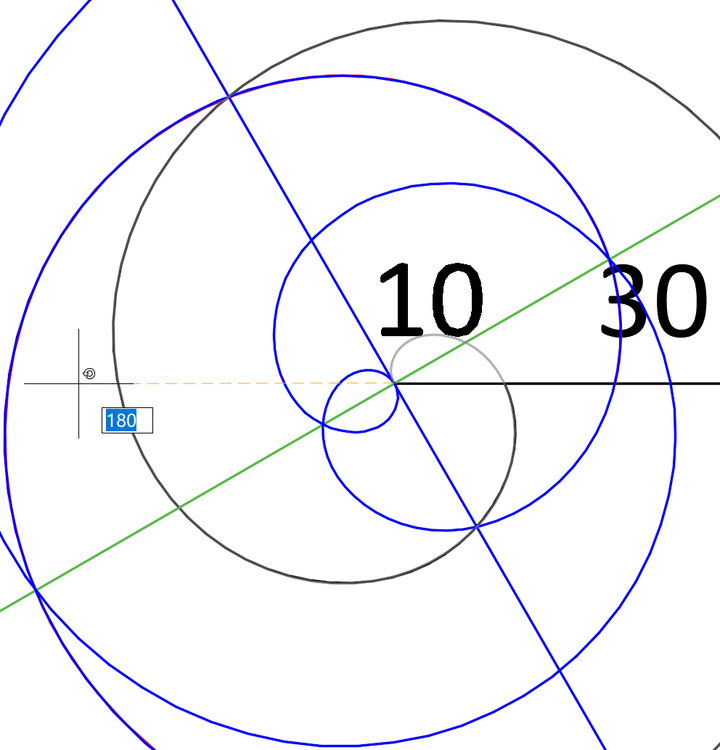
最终的效果如下图所示：

我们绘制出了红色螺旋向内连续进行螺旋运动时所形成的完整轨迹，同时也从多种角度证明了，Autocad中的螺旋无论内边、外边的半径怎样设置，它们始终还是属于阿基米德螺旋，不能用来实现渐开线以及风螺旋。

由于Autocad中的螺旋外扩或收缩的方向是穿过圆心的，所以它仍然是阿基米德螺旋。下次我们可以尝试一下在CAD中对渐开线及风螺旋线进行一下对比。

这届的学生有点可爱，不认识我的人可以猜猜看，答案很明显哦。

感谢你们的支持，希望等距螺旋之路越走越远~