ndt算法学习

　　NDT算法原理：

　　　　NDT算法的基本思想是先根据参考数据（reference scan）来构建多维变量的正态分布， 如果变换参数能使得两幅激光数据匹配的很好，那么变换点在参考系中的概率密度将会很大。

因此，可以考虑用优化的方法求出使得概率密度之和最大的变换参数，此时两幅激光点云数 据将匹配的最好。

算法流程：

1. 将空间（reference scan）划分成各个格子cell
2. 将点云投票到各个格子

3. 计算格子的正态分布PDF参数

   

4. 将第二幅scan的每个点按转移矩阵T的变换

5. 第二幅scan的点落于reference的哪个 格子，计算响应的概率分布函数

   

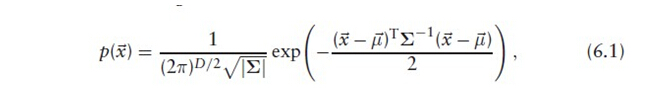
6. 求所有点的最优值，目标函数为

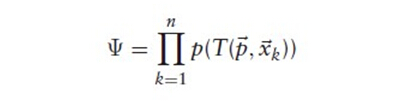
    NDT算法关键点：

1、将二维空间划分为固定大小网格，每个网格至少包括3个点（一般5个）

2、计算网格中点集的均值μ

3、计算网格中点集的协方差矩阵Σ

4、网格中的观测到点x的概率p(x)服从正态分布N( μ,Σ)。

 NDT关键代码示例：

    

1、加载输入点云和目标点云

auto target_cloud = read_cloud_point("cloud1.pcd");

auto input_cloud = read_cloud_point("cloud2.pcd");

2、点云滤波

approximate_voxel_filter.setLeafSize(0.5, 0.5, 0.5);

approximate_voxel_filter.setInputCloud(input_cloud);

approximate_voxel_filter.filter(*filtered_cloud);

3、配置点云参数

pcl::NormalDistributionsTransform<pcl::PointXYZ, pcl::PointXYZ> ndt;

ndt.setTransformationEpsilon(0.01); //收敛数

ndt.setStepSize(0.1); //步长

ndt.setResolution(1.0); //格子边长

ndt.setMaximumIterations(30); //迭代次数

ndt.setInputSource(filtered_cloud);

ndt.setInputTarget(target_cloud);

4、设置初始值

Eigen::AngleAxisf init_rotation(0.0, Eigen::Vector3f::UnitZ());

Eigen::Translation3f init_translation (0, 0, 0);

Eigen::Matrix4f init_guess = (init_translation * init_rotation).matrix();

5、开始配准

pcl::PointCloud<pcl::PointXYZ>::Ptr output_cloud (new pcl::PointCloud<pcl::PointXYZ>);

ndt.align(*output_cloud, init_guess);

6、保存配准的点云图

pcl::transformPointCloud(*input_cloud, *output_cloud, ndt.getFinalTransformation());

pcl::io::savePCDFileASCII("cloud3.pcd", *output_cloud);