[考试反思]1113csp-s模拟测试114：一梦

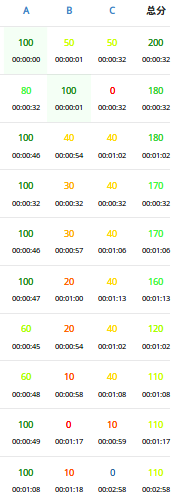
自闭。不废话。写一下低错。

T1：觉得信心赛T1不会很恶心一遍过样例直接没对拍（其实是想写完T2之后回来对拍的）

状态也不好，基本全机房都开始码了我还没想出来（skyh已经开T2了）。想了40多分钟。

区别不大。真是人才。

而且反向的单调栈没reverse。爆零。

T2：100多分钟打表找到了一个仅适用于n,a<=5的规律（我还以为它是普适的，但其实n<=5,a<=5也不完全对）。浪费时间太多。

这次说实在的不是故意刚它的，因为打表不断有新进展所以很开心就没看时间。

T3：最后7分钟写的暴力得了和前198分钟一样的分数。

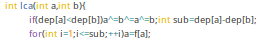
丢30分。求lca都不会打了。

真他妈难度中等有区分度看来我女队也混不了了2333。。。

把出题人挂起来婊

对自己没话可说了。那就干脆别废话了吧。

T1：A

可以发现，他给的二次函数没有c。有什么特性？一定经过原点？这个没什么用。

是可以整体除以x得到一次函数，正负分情况讨论。那么就剩下一个单调栈维护凸包板子。

写了对拍20分钟肯定是能调出来的。

 #include<cstdio>
 #include<algorithm>
 using namespace std;
 #define int long long
 struct line{
     int k,b;
     friend bool operator<(line A,line B){
         return A.k<B.k||(A.k==B.k&&A.b<B.b);
     }
 }l[];
 int ans[],sta[],top,negans[];
 int cal(int o,int x){return l[o].k*x*x+l[o].b*x;}
 long double mp(int o,int p){return (.0L+l[o].b-l[p].b)/(l[p].k-l[o].k);}
 main(){
     freopen("A.in","r",stdin);freopen("A.out","w",stdout);
     int n,q,x;scanf("%lld%lld",&n,&q);
     for(int i=;i<=n;++i)scanf("%lld%lld",&l[i].k,&l[i].b);
     sort(l+,l++n);
     for(int i=;i<=n;++i){
         while(top&&l[sta[top]].k==l[i].k&&l[sta[top]].b<l[i].b)top--;
         while(top&&mp(sta[top],i)<)top--;
         while(top>&&mp(sta[top-],sta[top])>=mp(sta[top-],i))top--;
         sta[++top]=i;
     }//for(int i=1;i<=top;++i)printf("%lld %lld\n",l[sta[i]].k,l[sta[i]].b);printf("%lld\n",l[2].k-l[3].k);
     int ptr=;
     for(int X=;X<;++X){
         while(ptr<top&&cal(sta[ptr],X)<=cal(sta[ptr+],X))ptr++;
         ans[X]=cal(sta[ptr],X);
     }
     top=;ptr=;
     for(int i=n;i;--i){
         while(top&&l[sta[top]].k==l[i].k&&l[sta[top]].b>l[i].b)top--;
         while(top>&&mp(sta[top-],sta[top])>=mp(sta[top-],i))top--;
         sta[++top]=i;
     }reverse(sta+,sta++top);
     for(int X=-;X>-;--X){
         while(ptr<top&&cal(sta[ptr],X)<=cal(sta[ptr+],X))ptr++;
         negans[-X]=cal(sta[ptr],X);
     }
     while(q--)scanf("%lld",&x),printf("%lld\n",x>=?ans[x]:negans[-x]);
 }

T2：B

除了第一个以外，其余的每一位是不互相影响的。

那么答案就是$a_1 + \sum\limits_{i=2)^{n} f(a_1,a_i) $

关键在于计算$f$函数。可以发现这个$f$函数的含义：

第一个物品被选完了，第二个物品期望被选多少个。

枚举它选了多少个，计算出概率，特殊处理被选完的情况，概率就是1-前面没被选的概率之和。

$f(a,b)=\sum\limits_{i=0}^{b-1} \frac{i \times C_{a+i-1}^{i}}{2^{a+i}} \ + b \ - \sum\limits_{i=0}^{b-1}\frac{b \times C_{a+i-1}^{i}}{2^{a+i}}$

+b前面的部分就是没选完，后面的部分就是选完了的剩余情况。组合数就是枚举这么多次选择恰好把它选完的方案数，除总方案数就是概率。

要-1的原因是最后一步要默认选择的是a而不是b。否则会重复计数。

再看本题的特殊之处，每次调用$f$函数的时候，第一个参数$a$都是一致的。

那么只要处理出来a这一列就好了。

可以发现，b每增大1，式子的变化之处并不多，前后的和式都多了一项。线性递推预处理即可。

 #include<cstdio>
 #include<iostream>
 using namespace std;
 #define int long long
 #define mod 323232323
 #define S 1000005
 int qpow(int b,int t,int a=){for(;t;t>>=,b=b*b%mod)if(t&)a=a*b%mod;return a;}
 int fac[S],inv[S],pw[S],ipw[S],F[S],G[S],ans,x;
 int C(int b,int t){return b<t?:fac[b]*inv[t]%mod*inv[b-t]%mod;}
 void f(){
     int totpos=;
     for(int i=;i<;++i){
         F[i]=((i?F[i-]:)+i*C(x-+i,i)%mod*ipw[x+i])%mod;
         totpos=(totpos+C(x-+i,i)*ipw[x+i])%mod;
         G[i]=(+i)*(+mod-totpos)%mod;
     }
     for(int i=S-;i;--i)F[i]=(F[i-]+G[i-])%mod;
 }
 main(){
     freopen("B.in","r",stdin);freopen("B.out","w",stdout);
     fac[]=;
     for(int i=;i<S;++i)fac[i]=fac[i-]*i%mod;
     inv[S-]=qpow(fac[S-],mod-);
     for(int i=S-;~i;--i)inv[i]=inv[i+]*(i+)%mod;
     pw[]=;
     for(int i=;i<S;++i)pw[i]=pw[i-]*%mod;
     ipw[S-]=qpow(pw[S-],mod-);
     for(int i=S-;~i;--i)ipw[i]=ipw[i+]*%mod;
     int n,y;scanf("%lld%lld",&n,&x);n--;ans=x;f();
     while(n--)scanf("%lld",&y),ans=(ans+F[y])%mod;
     printf("%lld\n",ans);
 }

T3：C

不想写。细节多，题解还那么垃圾。

$O(n\ log \ n \ log \ a_i)$的暴力看懂了。就是离线询问（否则会MLE）枚举每一位的答案贡献。

首先对于每次询问我们把或当成加法。求出路径上所有点的权值和，以及距离之和。

然后把或当成加法的多余贡献就是两个值相与的值，求出每个答案与后的值从上面那个值里扣除就是答案。

可以发现二进制串在递增序列上是有循环节的。先考虑u到lca的贡献。

处理数组dp[i][j]表示从i号节点开始的完整循环节的长度为$2^j$的祖先链上的当前处理的这一位的$a_i$值与循环节的1的撞上的数的个数。

然后对于非完整循环节特殊处理一下。我的想法是（强调：这是我自己yy的可能不对）：

再处理一个数组f[i][j]表示从i号点开始的长度为$2^j$的祖先链上的当前处理的这一位的$a_i$值为1的数的个数。也就是默认了距离值的这一位是1。

因为最后剩下的一段非完整循环节一定是一堆0，后面都是1。这样的话你倍增跳一下把0的都跳过，然后剩下的1用f数组就可以计算出来。

然后u到lca这一段就处理完了。对于v到lca的这一段，我们把v往上跳直到遇到第一个完整循环节开始的地方，这个跳可以类似的预处理。

然后剩下的就和u到lca一样了。只不过一个的循环是000011110000111100...这样的，另一个是111100001111000011....这样的。

那么你只要把前几个1排除在完整循环节之外进行处理，剩下的两边就完全一样了。

大神yxs写出来了得到了T70的好成绩（从上述代码细节你就可以感受到这题常数有多大）

心累。真心不想写。就这样吧。等yxs或其他大神AC之后我再update吧