LeetCode 51. N-QueensN皇后 (C++)(八皇后问题)

题目：

The n-queens puzzle is the problem of placing n queens on an n×n chessboard such that no two queens attack each other.

Given an integer n, return all distinct solutions to the n-queens puzzle.

Each solution contains a distinct board configuration of the n-queens' placement, where 'Q' and '.' both indicate a queen and an empty space respectively.

Example:

Input: 4
Output: [
 [".Q..",  // Solution 1
  "...Q",
  "Q...",
  "..Q."],

 ["..Q.",  // Solution 2
  "Q...",
  "...Q",
  ".Q.."]
]
Explanation: There exist two distinct solutions to the 4-queens puzzle as shown above.

分析：

n 皇后问题研究的是如何将 n 个皇后放置在 n×n 的棋盘上，并且使皇后彼此之间不能相互攻击。

给定一个整数 n，返回所有不同的 n 皇后问题的解决方案。

每一种解法包含一个明确的 n 皇后问题的棋子放置方案，该方案中 'Q' 和 '.' 分别代表了皇后和空位。

非常经典的问题，首先可以想到的是穷举所有皇后摆放的情况，来判断棋盘是否符合要求。但这样做肯定是会超时的。

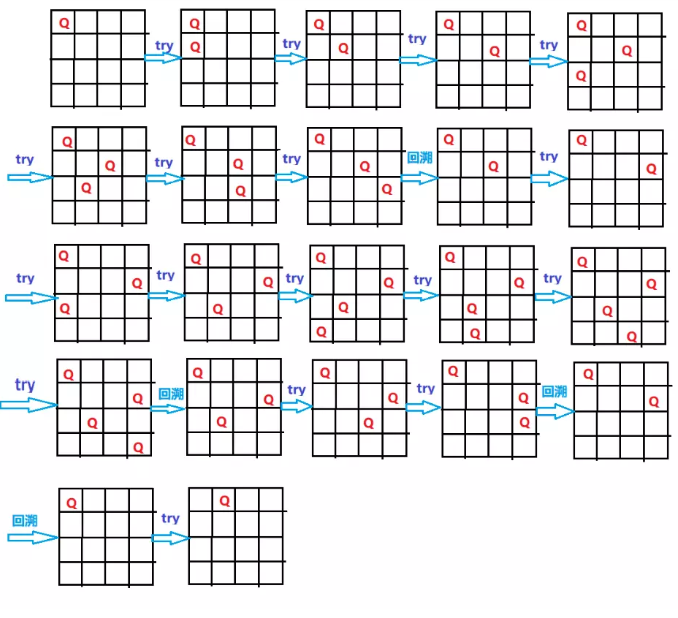
以n=4为例，我们构建一个二维数组sta，用来标识皇后能否放置，最开始皇后可以放置再任何地方，我们从第一行开始放置皇后，根据放置的位置，我们来修改sta数组(1为不能放置，0为可以放置)，将放置位置的行列以及两条对角线上的元素全部置1，之后在第二行放置皇后，并根据sta数组来判断当前位置皇后是否可以被放置，如果当前行搜索完毕后，都没有位置放置皇后，那么我们就要回到上一步放置皇后的状态，再去搜索下一个位置了。每次放置前要保存当前结果和当前判断数组(sta）以便回溯。

对于判断皇后放置的二维数组，可以换成一个列数组加上两个对角线数组来标记一个位置是否可以放置皇后，因为我们是一行一行来放置的，所以不存在某一行出现两个皇后，所以当一列放置了一个皇后时，该列标记为不可放置(col[i]=1，即第i列已经有皇后了)，对角线可以对照下图：

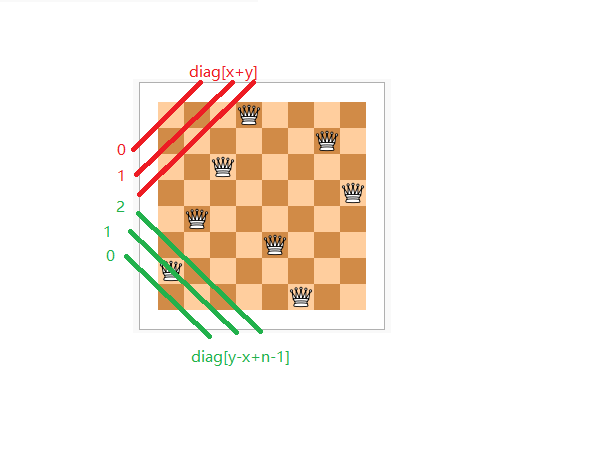
[x,y]位置对应从左下角至右上角的对角线diag1[x+y]，而对应从左上角至右下角的对角线diag2[y-x+n-1]，这样每一个位置能否放置皇后判断的条件都有了，不用再使用一个棋盘大小的二维数组来标识了。

程序：

class Solution {
public:
    void update(int n, vector<vector<int>> &vec, int x, int y){
        for(int i = ; i < n; ++i){
            vec[i][y] = ;
            vec[x][i] = ;
        }
        int i = ,j = ;
        for(i = x, j = y; i < n && j < n; ++i, ++j){
            vec[i][j] = ;
        }
        for(i = x, j = y; i >=  && j >= ; --i, --j){
            vec[i][j] = ;
        }
        for(i = x, j = y; i < n && j >= ; ++i, --j){
            vec[i][j] = ;
        }
        for(i = x, j = y; i >=  && j < n; --i, ++j){
            vec[i][j] = ;
        }
        return;
    }
    void queen(int n, int y, vector<string> &temp_res, vector<vector<int>> &sta){
        if(y == n){
            res.push_back(temp_res);
            return;
        }
        for(int j = ; j < n; ++j){
                if(sta[y][j] == ){
                    vector<string> temp2 = temp_res;
                    temp_res[y][j] = 'Q';
                    vector<vector<int>> temp = sta;
                    update(n, sta, y, j);
                    queen(n, y+, temp_res, sta);
                    sta = temp;
                    temp_res = temp2;
                }
                else
                    continue;
            }
        return;
    }
    vector<vector<string>> solveNQueens(int n) {
        vector<string> temp_res(n, string(n, '.'));
        vector<vector<int>> sta(n, vector<int>(n,));
        queen(n, , temp_res, sta);
        return res;
    }
private:
    vector<vector<string>> res;
};

class Solution {
public:
    void queen(int n, int x, vector<string> &temp_res){
        if(x == n){
            res.push_back(temp_res);
            return;
        }
        for(int y = ; y < n; ++y){
                if(col[y] ==  && diag1[x+y] ==  && diag2[y-x+n-] == ){
                    temp_res[x][y] = 'Q';
                    col[y] = ;
                    diag1[x+y] = ;
                    diag2[y-x+n-] = ;
                    queen(n, x+, temp_res);
                    temp_res[x][y] = '.';
                    col[y] = ;
                    diag1[x+y] = ;
                    diag2[y-x+n-] = ;
                }
                else
                    continue;
            }
        return;
    }
    vector<vector<string>> solveNQueens(int n) {
        vector<string> temp_res(n, string(n, '.'));
        col = vector<int>(n, );
        diag1 = vector<int>( * n - , );
        diag2 = vector<int>( * n - , );
        queen(n, , temp_res);
        return res;
    }
private:
    vector<vector<string>> res;
    vector<int> col;
    vector<int> diag1;
    vector<int> diag2;
};