机器学习---用python实现最小二乘线性回归算法并用随机梯度下降法求解 （Machine Learning Least Squares Linear Regression Application SGD）

在《机器学习---线性回归（Machine Learning Linear Regression）》一文中，我们主要介绍了最小二乘线性回归算法以及简单地介绍了梯度下降法。现在，让我们来实践一下吧。

先来回顾一下用最小二乘法求解参数的公式：。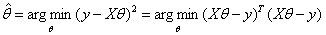

（其中：，，）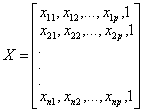

再来看一下随机梯度下降法（Stochastic Gradient Descent）的算法步骤：

除了算法中所需的超参数α（学习速率，代码中写为lr）和epsilon（误差值），我们增加了另一个超参数epoch（迭代次数）。此外，为方便起见，在代码中我们用w代替θ。

我们自己创建了一组数据，是最简单的一元线性回归，以便画图展示。由于整个过程基本上就是上述算法步骤的重复，故在此次不一一分解了，请自行查看完整代码。至于学习速率alpha的选择，请查看：如何选择梯度下降法中的学习速率α（Gradient Descent Alpha）。

完整代码如下：

import matplotlib.pyplot as plt
fig,ax=plt.subplots()
import numpy as np

#创建数据
x=np.linspace(0,100,10).reshape(10,1)
rng=np.random.RandomState(4)
noise=rng.randint(-10,10,size=(10,1))*4
y=4*x+4+noise

class Linear_Regression:
    def __init__(self):
        self._w = None

    def fit(self, X, y, lr=0.01, epsilon=0.01, epoch=1000):
        #训练数据
        #将输入的X,y转换为numpy数组
        X, y = np.asarray(X, np.float32), np.asarray(y, np.float32)
        #给X增加一列常数项
        X=np.hstack((X,np.ones((X.shape[0],1))))
        #初始化w
        self._w = np.zeros((X.shape[1],1)) 

        for _ in range(epoch):
            #随机选择一组样本计算梯度
            random_num=np.random.choice(len(X))
            x_random=X[random_num].reshape(1,2)
            y_random=y[random_num]

            gradient=(x_random.T)*(np.dot(x_random,self._w)-y_random)

            #如果收敛，那么停止迭代
            if (np.abs(self._w-lr*gradient)<epsilon).all():
                break
            #否则，更新w
            else:
                self._w =self._w-lr*gradient          

        return self._w

    def print_results(self):
        print("参数w:{}".format(self._w))
        print("回归拟合线:y={}x+{}".format(self._w[0],self._w[1]))

    def draw_pics(self,X):
       #画出原始数据
       ax.scatter(X,y,marker="o")
       ax.set_xlabel("x")
       ax.set_ylabel("y")

       #画出拟合线
       line_x=np.linspace(0,100,10)
       line_y=self._w[0]*line_x+self._w[1]
       ax.plot(line_x,line_y) 

    def predict(self,x):
        x=np.asarray(x, np.float32)
        x=x.reshape(x.shape[0],1)
        x=np.hstack((x,np.ones((x.shape[0],1))))
        return np.dot(x,self._w)

if __name__=="__main__":
    Regression=Linear_Regression()
    Regression.fit(x,y,lr=0.0001,epsilon=0.001,epoch=20)
    Regression.print_results()
    Regression.draw_pics(x)

运行结果：

参数w:[[3.95933261]
 [0.06683964]]
回归拟合线:y=[3.95933261]x+[0.06683964]

画出的拟合线：