关于DML的一些使用

DML是一种非常简单的标记语言，它帮助基于现有命令的输出发现和执行新命令。许多WinDbg命令（以及扩展命令）都支持DML。例如，下面是lm D命令，它显示DML输出：

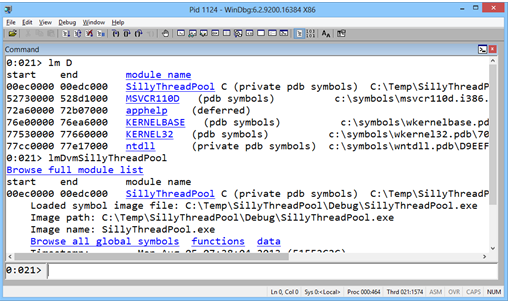
在上面的命令输出中，当我单击“SillyThreadPool”链接时，调试器为我执行了另一个命令lmDvmSillyThreadPool，它显示模块信息。同样，还有一个链接缺陷可以帮助我探索该模块中的符号和函数。

第一件事。您不必记住一堆奇怪的命令后缀就可以得到DML输出。有一个全局开关可以打开，.prefer_dml 1，这会导致许多内置命令和扩展命令显示dml输出。例如，下面是打开该开关后kn命令的输出：

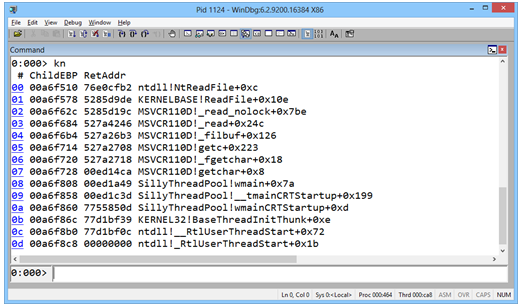
单击时，此处的链接将切换到该帧并显示源代码和本地变量（执行的命令是.frame 0nN；dv/t/v）。
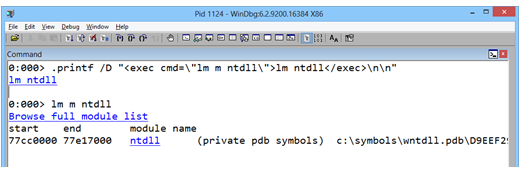
调试器脚本和扩展也可以生成DML输出。在调试器脚本中，只需使用.printf/D命令，并在其中嵌入DML链接。在调试器扩展中，可以使用IDebugClient：：ControlledOutput函数输出DML。例如，下面显示单击时执行另一个命令的链接：

.printf /D "<exec cmd=\"lm m ntdll\">lm ntdll</exec>\n\n"

我敢打赌你不知道。应用程序本身可以向调试器输出DML命令！只需要使用outputDebugStringAPI，并在其中嵌入神奇的字符串<?dml?>. 该魔法令牌之后的所有内容都将被解释为DML字符串，并相应地显示在调试器中。例如，假设我们的应用程序中有以下代码：

OutputDebugString(L"Entered thread pool demo app.\n<?dml?><exec cmd=\"!uniqstack\">Dump unique stacks</exec>\n");

然后，调试器遇到此调试输出时将显示命令链接：

下一个命令是.dml_flow。此命令旨在通过将反汇编函数拆分为代码块并帮助使用DML链接在块之间导航，使其更易于读取。你自己试验这个命令比我用语言解释要容易得多，但总的来说，你提供了两个地址——一个开始地址和一个目标地址——这个命令帮助你理解从开始地址可以到达目标的代码路径。

前一个屏幕截图中的链接指向进入和退出屏幕上显示的基本代码块的跳转路径。

与DML有关的最后一个命令是discovery命令，.DML_start。此命令接受一个包含许多DML链接和命令描述的文件，并将其显示在调试器窗口中（这与命令浏览器窗口结合使用非常方便）。例如，假设您有以下文件：

Load SOS according to the CLR version that is currently in the process.
    <link cmd=".loadby sos clr; .loadby sos mscorwks">Load SOS</link>

Display the last event and CLR exception.
    <link cmd=".lastevent">Last debugger event</link>
    <link cmd="!PrintException">Last CLR exception</link>

Display the CLR call stack for a specific thread.
    <b>~<i>N</i>s; !CLRStack</b>
    Example: <link cmd="~0s; !CLRStack">~0s; !CLRStack</link>

执行.browse.dml_start dn.dml会产生以下结果：

这是一个方便的命令浏览器，您可以使用它开始调查。我还认为它对于解释您在dump分析会话中所采取的步骤非常有用