机器学习（4）——PCA与梯度上升法

主成分分析（Principal Component Analysis）

1. 一个非监督的机器学习算法
2. 主要用于数据的降维
3. 通过降维，可以发现更便于人类理解的特征
4. 其他应用：可视化、去噪

通过映射，我们可以把数据从二维降到一维：

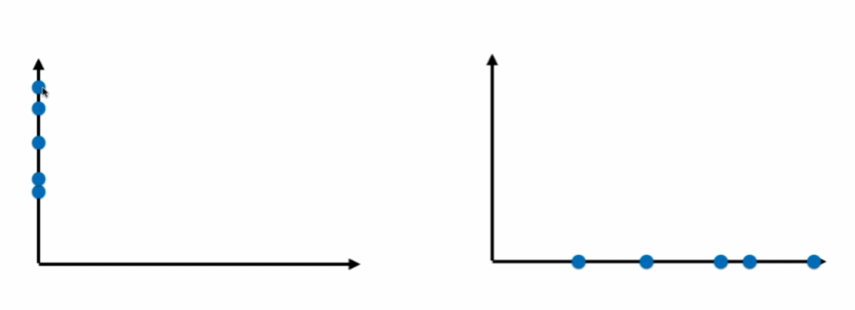
显然，右边的要好一点，因为间距大，更容易看出差距。

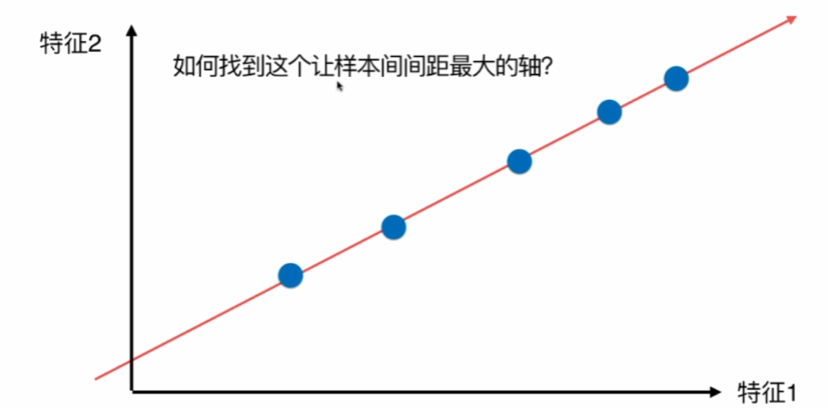
如何定义样本间距？使用方差，因为方差越小，数据月密集，方差越大，数据月分散。

另均值为0：

因为均值为0，w是单位向量，模为1，所以：

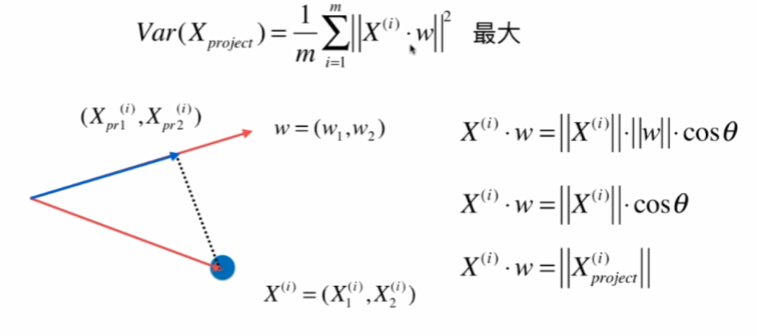
梯度上升法求解PCA问题

分析：X是mn的矩阵，m是样本数，n是特征数，X^(i)是第i个样本，w是n * 1 的矩阵，那么这n个∑X^(i) * w就等于Xw （m行1列）

import numpy as np
import matplotlib.pyplot as plt

X=np.empty((100,2)) #100行2列
X[:,0]=np.random.uniform(0.,100.,size=100) #100个0~100的均匀分布点
X[:,1]=0.75*X[:,0]+3.+np.random.normal(0,10.,size=100) #100个均值为0，标准差为10的正态分布点

plt.scatter(X[:,0],X[:,1])
plt.show()

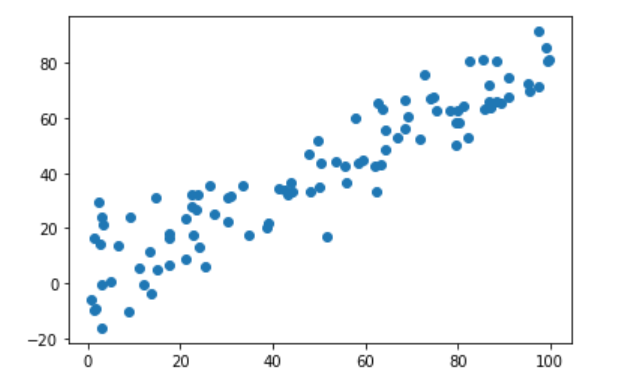
demean（每一维的样本均值归0）：

def demean(X):
    return X-np.mean(X,axis=0)#对X的每一列的每个数减去这一列的均值，即可让X的每一列均值变为0

X_demean=demean(X)

plt.scatter(X_demean[:,0],X_demean[:,1])
plt.show()

np.mean(X_demean[:,0])

np.mean(X_demean[:,1])

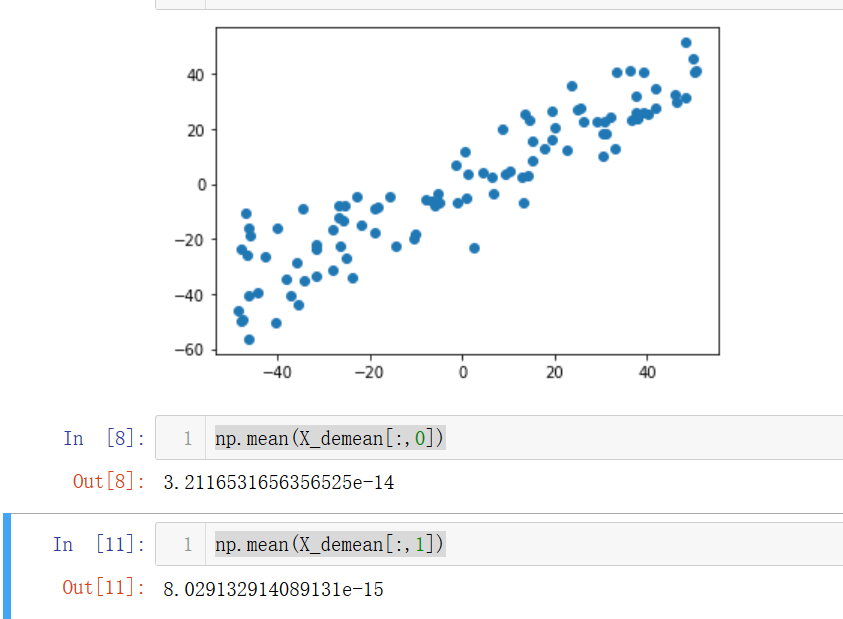
发现两个维度的均值都几乎为0。

梯度上升：

def f(w,X):
    return np.sum((X.dot(w)**2))/len(X)

def df_math(w,X):
    return X.T.dot(X.dot(w))*2./len(X)

def df_debug(w,X,epsilon=0.0001): #调试梯度
    res=np.empty(len(w))
    for i in range(len(w)):
        w_1=w.copy()
        w_1[i]+=epsilon
        w_2=w.copy()
        w_2[i]-=epsilon
        res[i]=(f(w_1,X)-f(w_2,X))/(2*epsilon)
    return res

def direction(w):#化成单位向量
    return w/np.linalg.norm(w) #除以w的模即可

def gradient_ascent(df,X,initial_w,eta,n_iters=1e4,epsilon=1e-8):
    #梯度上升法
    w=direction(initial_w)
    cur_iter=0
    while cur_iter < n_iters:
        gradient = df(w,X)
        last_w=w
        w=w+eta*gradient #变成加法
        w=direction(w) #注意1：化成单位向量
        if(abs(f(w,X)-f(last_w,X))<epsilon):
            break
        cur_iter+=1

    return w 

initial_w=np.random.random(X.shape[1]) #注意2：不能用0向量开始，不然求导的时候也是0

eta=0.001
#注意3：不能使用StandardScaler标准化数据，因为我们要使方差最大，而不是为1

gradient_ascent(df_debug,X_demean,initial_w,eta) #调试求出的梯度

gradient_ascent(df_math,X_demean,initial_w,eta)#推导的公式求梯度

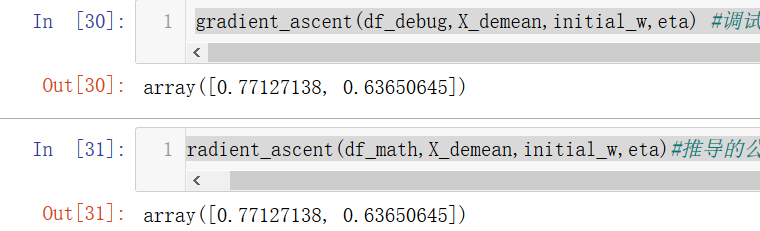
发现一模一样，说明求导公式是正确的。

w=gradient_ascent(df_math,X_demean,initial_w,eta)#推导的公式求梯度
plt.scatter(X_demean[:,0],X_demean[:,1])
plt.plot([0,w[0]*30],[0,w[1]*30],color="r")
#第一个参数是横坐标数组，第二个参数是纵坐标数组，因为w是单位向量，太小了，所以*30变大一点
plt.show()

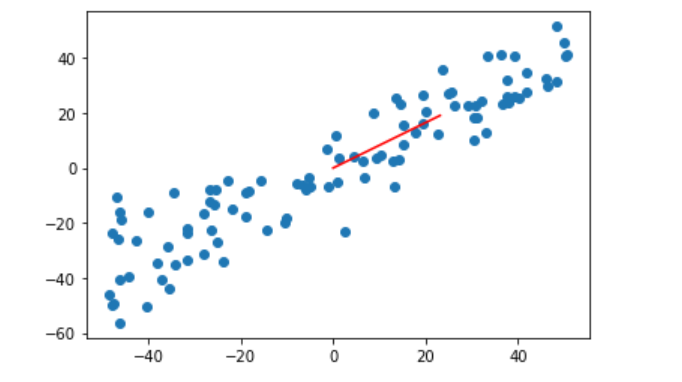
测试一下不加噪音是否正确：

X2=np.empty((100,2)) #100行2列
X2[:,0]=np.random.uniform(0.,100.,size=100) #100个0~100的均匀分布点
X2[:,1]=0.75*X2[:,0]+3.#不加噪音

plt.scatter(X2[:,0],X2[:,1])
plt.show()

X2_demean=demean(X2)

gradient_ascent(df_math,X2_demean,initial_w,eta)

w2=gradient_ascent(df_math,X2_demean,initial_w,eta)

plt.scatter(X2_demean[:,0],X2_demean[:,1])
plt.plot([0,w2[0]*30],[0,w2[1]*30],color="r")
plt.show()

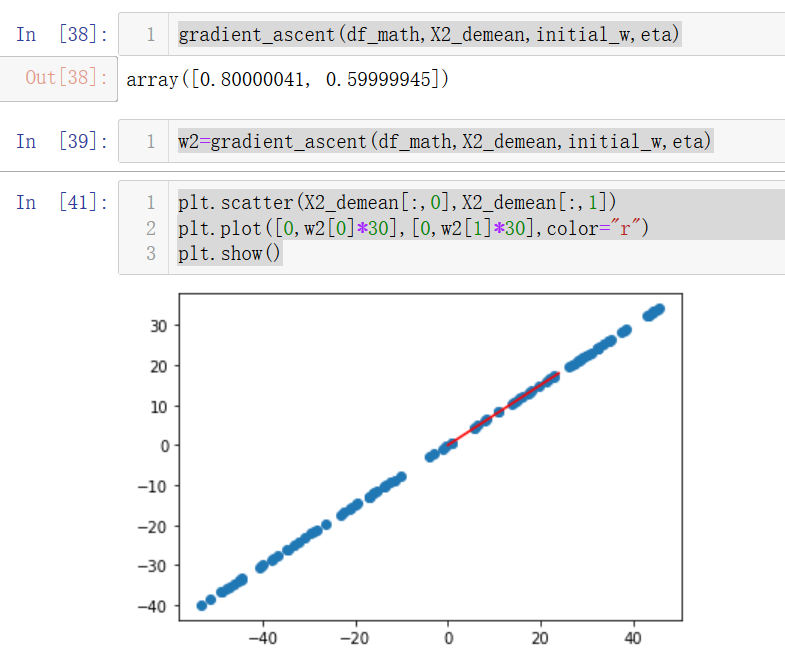
因为我们设置的斜率是0.75，而这里求出的w=[0.8,0.6]，对边/斜边=0.75，说明梯度上升是正确的。

求数据的前n个主成分

求出第一个主成分以后，如何求出下一个主成分？

数据进行改变，将数据在第一个主成分上的分量去掉，再在新的数据求第一主成分。

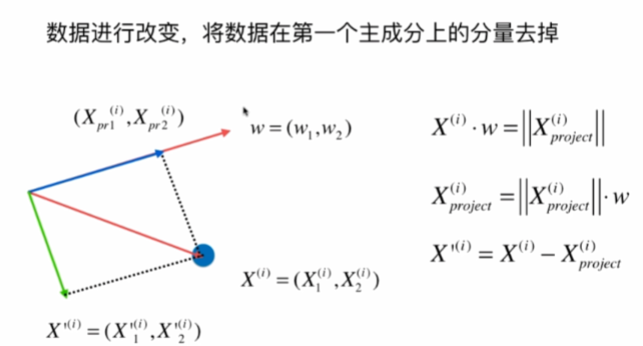
numpy中一维数组的运算的一些奇妙的地方：

https://blog.csdn.net/xo3ylAF9kGs/article/details/78623276

import numpy as np
import matplotlib.pyplot as plt

X=np.empty((100,2)) #100行2列
X[:,0]=np.random.uniform(0.,100.,size=100) #100个0~100的均匀分布点
X[:,1]=0.75*X[:,0]+3.+np.random.normal(0,10.,size=100) #100个均值为0，标准差为10的正态分布点
def demean(X):
    return X-np.mean(X,axis=0)#对X的每一列的每个数减去这一列的均值，即可让X的每一列均值变为0

X=demean(X)

def f(w,X):
    return np.sum((X.dot(w)**2))/len(X)
def df(w,X):
    return X.T.dot(X.dot(w))*2./len(X)
def direction(w):#化成单位向量
    return w/np.linalg.norm(w) #除以w的模即可

def first_component(X,initial_w,eta,n_iters=1e4,epsilon=1e-8):
    #梯度上升法
    w=direction(initial_w)
    cur_iter=0
    while cur_iter < n_iters:
        gradient = df(w,X)
        last_w=w
        w=w+eta*gradient #变成加法
        w=direction(w) #注意1：化成单位向量
        if(abs(f(w,X)-f(last_w,X))<epsilon):
            break
        cur_iter+=1

    return w 

initial_w=np.random.random(X.shape[1])
eta=0.01
w=first_component(X,initial_w,eta)

X2=X-X.dot(w).reshape(-1,1)*w #点积后变成m行1列再和w数组（n个元素）每个元素对应相乘，形成m行n列的矩阵

plt.scatter(X2[:,0],X2[:,1])
plt.show()

对第二维主成分分析的结果：

w2=first_component(X2,initial_w,eta)
w2

w.dot(w2)

点积之后几乎为0，说明是正确的，因为两个方向是垂直的。

求前n个主成分：

def first_n_components(n,X,eta=0.01,n_iters=1e4,epsilon=1e-8):
    X_pca=X.copy()
    X_pca=demean(X_pca)
    res=[]
    for i in range(n):
        initial_w=np.random.random(X_pca.shape[1])
        w=first_component(X_pca,initial_w,eta)
        res.append(w)
        X_pca=X_pca-X_pca.dot(w).reshape(-1,1)*w
    return res

first_n_components(2,X)

高维数据向低维数据映射

将n为数据映射到k维

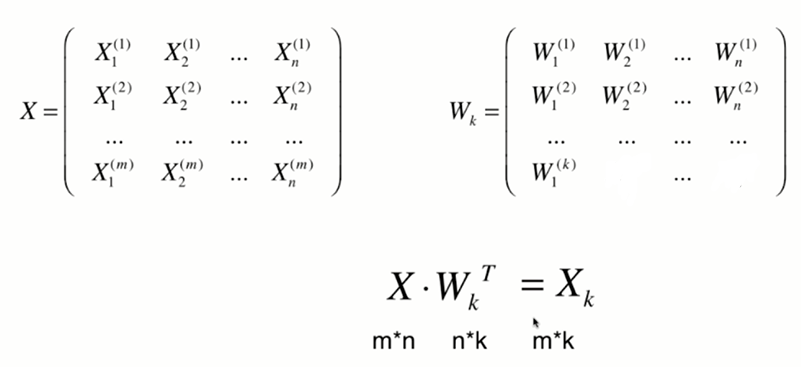
将k维数据恢复到n维：

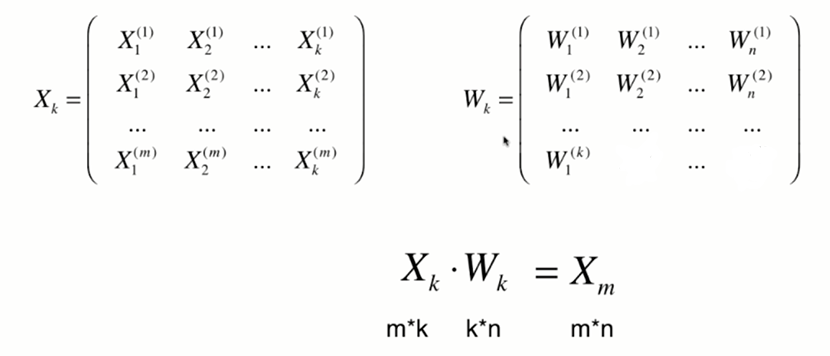
import numpy as np

class PCA:

    def __init__(self, n_components):
        """初始化PCA"""
        assert n_components >= 1, "n_components must be valid"
        self.n_components = n_components
        self.components_ = None

    def fit(self, X, eta=0.01, n_iters=1e4):
        """获得数据集X的前n个主成分"""
        assert self.n_components <= X.shape[1], \
            "n_components must not be greater than the feature number of X"

        def demean(X):
            return X - np.mean(X, axis=0)

        def f(w, X):
            return np.sum((X.dot(w) ** 2)) / len(X)

        def df(w, X):
            return X.T.dot(X.dot(w)) * 2. / len(X)

        def direction(w):
            return w / np.linalg.norm(w)

        def first_component(X, initial_w, eta=0.01, n_iters=1e4, epsilon=1e-8):

            w = direction(initial_w)
            cur_iter = 0

            while cur_iter < n_iters:
                gradient = df(w, X)
                last_w = w
                w = w + eta * gradient
                w = direction(w)
                if (abs(f(w, X) - f(last_w, X)) < epsilon):
                    break

                cur_iter += 1

            return w

        X_pca = demean(X)
        self.components_ = np.empty(shape=(self.n_components, X.shape[1]))
        for i in range(self.n_components):
            initial_w = np.random.random(X_pca.shape[1])
            w = first_component(X_pca, initial_w, eta, n_iters)
            self.components_[i,:] = w

            X_pca = X_pca - X_pca.dot(w).reshape(-1, 1) * w

        return self

    def transform(self, X):
        """将给定的X，映射到各个主成分分量中"""
        assert X.shape[1] == self.components_.shape[1]

        return X.dot(self.components_.T)

    def inverse_transform(self, X):
        """将给定的X，反向映射回原来的特征空间"""
        assert X.shape[1] == self.components_.shape[0]

        return X.dot(self.components_)

    def __repr__(self):
        return "PCA(n_components=%d)" % self.n_components

import numpy as np
import matplotlib.pyplot as plt

X=np.empty((100,2)) #100行2列
X[:,0]=np.random.uniform(0.,100.,size=100) #100个0~100的均匀分布点
X[:,1]=0.75*X[:,0]+3.+np.random.normal(0,10.,size=100) #100个均值为0，标准差为10的正态分布点

%run f:\python3玩转机器学习\PCA与梯度上升法\PCA.py 

pca=PCA(n_components=2)
pca.fit(X)

pca=PCA(n_components=1)
pca.fit(X)

X_reduction=pca.transform(X)

X_restore=pca.inverse_transform(X_reduction)

plt.scatter(X[:,0],X[:,1],color="b",alpha=0.5)
plt.scatter(X_restore[:,0],X_restore[:,1],color='r',alpha=0.5)
plt.show()

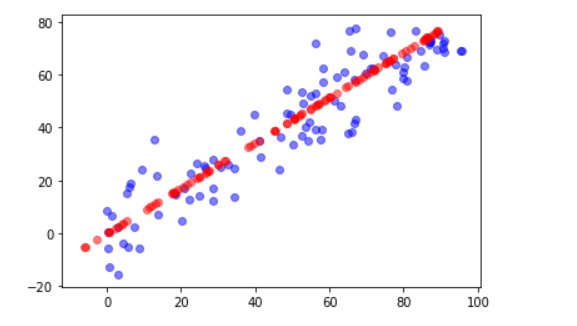
红色的线是恢复后的数据，可见丢失了一些信息。

scikit-learn中的PCA

先接着用上面的数据，

from sklearn.decomposition import PCA

pca = PCA(n_components=1)
pca.fit(X)

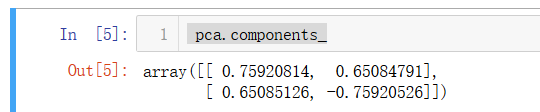
pca.components_

咦？怎么跟我们上面求的第一主成分不太一样，但是斜率是差不多的，这是因为scikit-learn中的PCA是通过数学推导的，不是我们上面用的梯度上升法。

X_reduction=pca.transform(X)
X_restore=pca.inverse_transform(X_reduction)
plt.scatter(X[:,0],X[:,1],color="b",alpha=0.5)
plt.scatter(X_restore[:,0],X_restore[:,1],color="r",alpha=0.5)
plt.show()

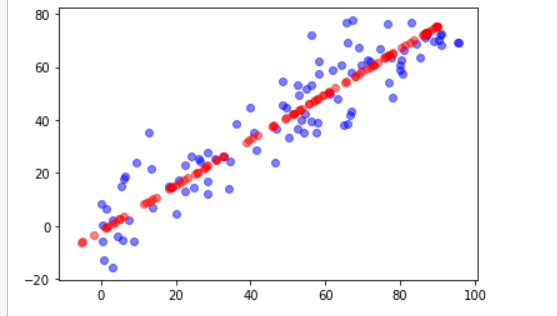
最后绘制出来的图跟上面的方法是差不多的。

再玩一下手写字母识别这个数据集：

import numpy as np
import matplotlib.pyplot as plt
from sklearn import datasets

digits=datasets.load_digits()
X=digits.data
y=digits.target

from sklearn.model_selection import train_test_split
X_train,X_test,y_train,y_test=train_test_split(X,y,random_state=666)

%%time
from sklearn.neighbors import KNeighborsClassifier

knn_clf=KNeighborsClassifier()
knn_clf.fit(X_train,y_train)

knn_clf.score(X_test,y_test)

直接降到二维试试（斜眼笑）：

from sklearn.decomposition import PCA
pca=PCA(n_components=2) #从64维降到2维
pca.fit(X_train)
X_train_reduction=pca.transform(X_train)
X_test_reduction=pca.transform(X_test)

%%time
knn_clf=KNeighborsClassifier()
knn_clf.fit(X_train_reduction,y_train)

哇！居然只用了1ms。

knn_clf.score(X_test_reduction,y_test)

但这正确率也太低了吧。。。虽然运行速度提高了，但精度低了。

pca.explained_variance_ratio_ #这两维显示所占的方差比，大概只有28%，所以精度很低

先直接算一下64维各维方差占比的情况：

pca=PCA(n_components=X_train.shape[1])
pca.fit(X_train)
pca.explained_variance_ratio_ #从大到小排序的

plt.plot([i for i in range(X_train.shape[1])],
        [np.sum(pca.explained_variance_ratio_[:i+1]) for i in range(X_train.shape[1])])
plt.show()

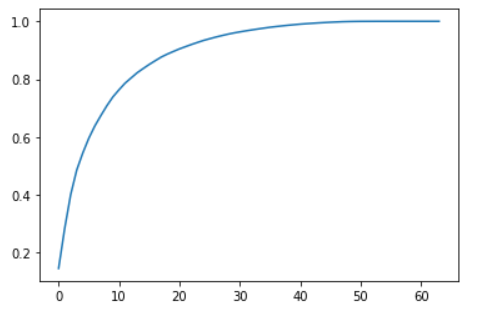
横轴为维度，纵轴为我们需要的方差占比。

如果我们想要方差占比0.95：

pca=PCA(0.95)
pca.fit(X_train)

pca.n_components_

输出28，所以我们要用PCA降到28维：

X_train_reduction=pca.transform(X_train)
X_test_reduction=pca.transform(X_test)

%%time
knn_clf=KNeighborsClassifier()
knn_clf.fit(X_train_reduction,y_train)

好快啊！

knn_clf.score(X_test_reduction,y_test)

正确率也好高啊！！！

看来28维足以兼并精度和时间~

我们再看看PCA降到二维可视化：

pca=PCA(n_components=2)
pca.fit(X)
X_reduction=pca.transform(X)

for i in range(10):
    plt.scatter(X_reduction[y==i,0],X_reduction[y==i,1],alpha=0.8)#每次循环自动换颜色
plt.show()

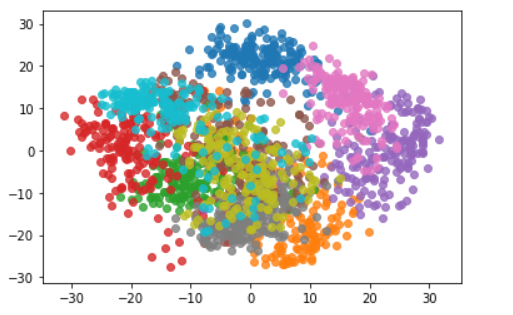
可以发现不同的类别降到二维后还是可以区分的，比如我们需要区分粉色和紫色，那么降到二维就足够应对了。

MNIST数据集

下载MNIST数据集可能会出现超时状况，解决办法：https://blog.csdn.net/qq_41312839/article/details/86671939

import numpy as np
from sklearn.datasets import fetch_mldata

mnist=fetch_mldata("MNIST original")

X,y=mnist['data'],mnist['target']
X_train=np.array(X[:60000],dtype=float)#mnist数据集前60000个是训练数据
y_train=np.array(y[:60000],dtype=float)
X_test=np.array(X[60000:],dtype=float)
y_test=np.array(y[60000:],dtype=float)

from sklearn.neighbors import KNeighborsClassifier
knn_clf=KNeighborsClassifier() #scikit-learn中的KNN对于数据大时会使用KD-tree或BALL-tree来加速
%time knn_clf.fit(X_train,y_train)

%time knn_clf.score(X_test,y_test)

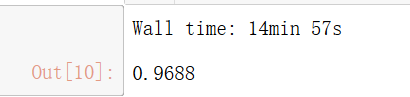
预测时间是真的太长了。。我们再看看PCA降维的结果吧：

from sklearn.decomposition import PCA
pca=PCA(0.9)#保留90%的信息
pca.fit(X_train)
X_train_reduction=pca.transform(X_train)

knn_clf=KNeighborsClassifier()
%time knn_clf.fit(X_train_reduction,y_train)

X_test_reduction=pca.transform(X_test)

%time knn_clf.score(X_test_reduction,y_test)

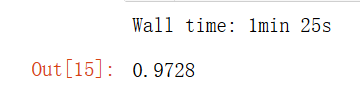
可以发现，降维后时间提高了很多，准确率居然也上升了，这是因为PCA具有降噪的功能。

PCA还可以应用于手写识别、人脸识别领域。