多目标跟踪笔记二：Efficient Algorithms for Finding the K Best Paths Through a Trellis

Abstract

　　本文提出了一种新的方法来寻找不相交k最优路径。最坏情况下计算复杂度为N³log(N)。该方法比WVD算法（https://www.cnblogs.com/walker-lin/p/11051983.html）速度更快。

Introduction

　　WVD算法中，计算复杂度随着虚警（false alarms）的增加呈指数增加，这限制了算法适用更多的场景。

　　本文提出的算法are based on a transformation of the K-path trellis problem into an equivalent minimum cost nenvork flow (MCNF) problem。而解决MCNF问题的复杂度随着measurements总数的增加呈多项式增加。
equivalent minimum cost nenvork flow formultion

　　不相交k最优路径：a）不相交；b）k条路径的总成本最少。

　　

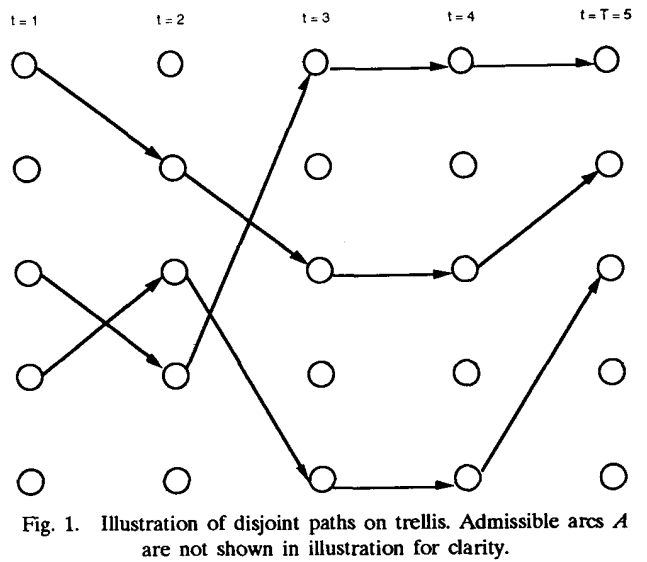
　　1）如果满足：

　　　　a）不要求路径不相交；

　　　　b）添加第0层和第T+1层，第0层和第T+1层都只有一个node；第0层到第1层、第T层到第T+1层的arc cost都为0；

　　　　c）第0层有K个单位的输入flow，第T+1层有k个单位的输出flow。

　　　　则不相交k最优路径问题 → MCNF问题：

　　　　

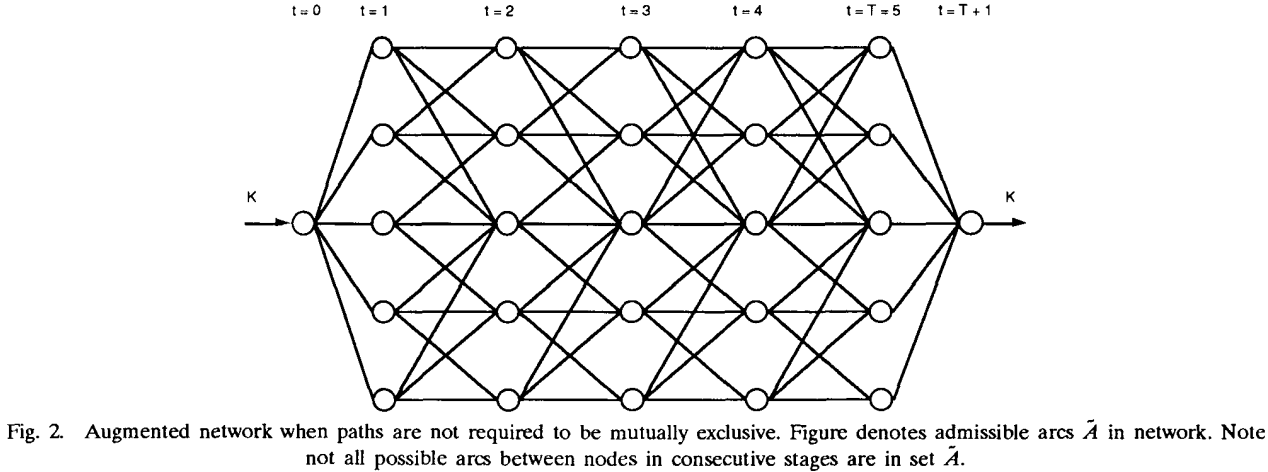
　　　　此时，k最优路径（不要求不相交）转换为：

　　　　

　　　　

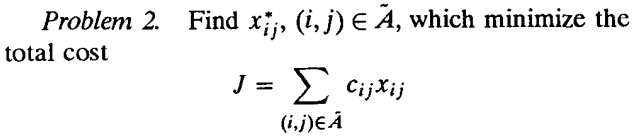
　　　　其中，x_ij表示arc flow，c_ij表示arc cost。

　　2）为了满足不相交约束，for each set N_t,t = 2,...,T- 1, 对每一个node添加一个对应node*，且node到node*的arc cost等于0，
　　　　

　　　　

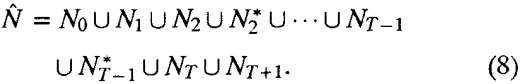
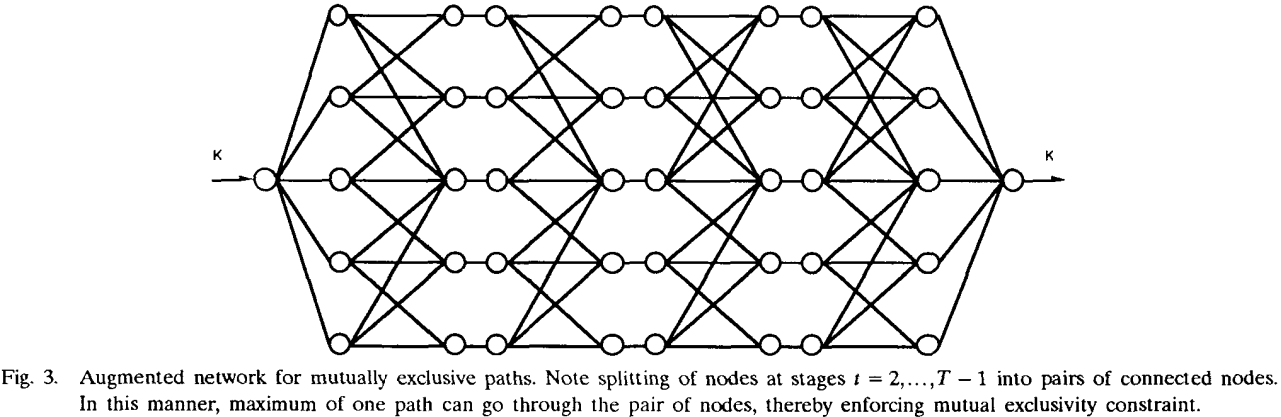
　　　　那么，不相交k最优路径可以转换为以下问题：

　　　　

　　　　

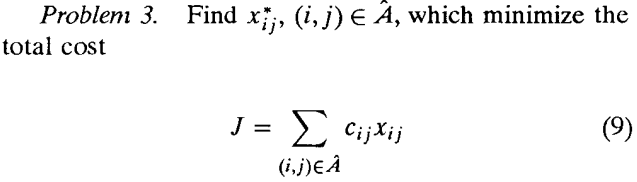
　　　　n_t中的node最多被使用一次。

算法性能比较

　　假设N_t=M，t=1,2,......,T。

　　算法1：WVD算法；算法2：ε-relaxation algorithm in [Dual coordinate step methods for linear network flow problems]。

　　计算法复杂度：

　　　　算法1：O(W),其中；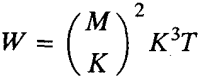

　　　　算法2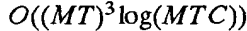：，其中C是c_ij的最大值。

　　空间复杂度：

　　　　算法1：O(V),其中；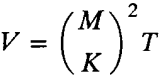

　　　　算法2：O(M²T)