Python----DFS---骑士周游问题

这篇文章将会将一个数据结构与算法中一个很经典很重要的概念——深度优先搜索（Depth-First-Search：DFS）。。。。。。。。。（你他喵不是在标题里说了吗？）

好吧，DFS的精髓我其实也还没有弄的特别懂，估计得多用用才能理解更深吧。

！！！敲黑板！！！DFS的关键是递归，递归是真好用！！！

---

深度优先搜索（DFS）

什么是DFS呢，秉着能动手就绝不吵吵的原则，直接给出网上大神的博文链接：http://www.cnblogs.com/skywang12345/p/3711483.html

好吧，其实这种链接你自己都能百度到的。我就放这里做个参考，我的主要目的还是要讲一下骑士周游问题。

骑士周游问题

骑士周游问题的主要内容是什么呢？不是废话，直接上网址：http://blog.fishc.com/2554.html，这个页面对DFS问题说明的非常清楚。作者是小甲鱼大神，我在B站看的就是他的数据结构课程，不时的开个车差点闪了我的腰。

特喵的，不是说好的不说废话吗？（我错了，好吧）

好吧，直接上代码：

import datetime
from enum  import Enum

class Size(Enum):
    X = 8

start = datetime.datetime.now()
chess = [[0 for i in range(Size.X.value)]for j in range(Size.X.value)]

def nextXY(x, y, position):
    global chess
    if position==0 and x-2>=0 and y-1>=0 and chess[x-2][y-1]==0:
        return [1, x-2, y-1]
    elif position==1 and x-2>=0 and y+1<=Size.X.value-1 and chess[x-2][y+1]==0:
        return [1, x-2, y+1]
    elif position==2 and x-1>=0 and y-2>=0 and chess[x-1][y-2]==0:
        return [1, x-1, y-2]
    elif position==3 and x-1>=0 and y+2<=Size.X.value-1 and chess[x-1][y+2]==0:
        return [1, x-1, y+2]
    elif position==4 and x+1<=Size.X.value-1 and y-2>=0 and chess[x+1][y-2]==0:
        return [1, x+1, y-2]
    elif position==5 and x+1<=Size.X.value-1 and y+2<=Size.X.value-1 and chess[x+1][y+2]==0:
        return [1, x+1, y+2]
    elif position==6 and x+2<=Size.X.value-1 and y-1>=0 and chess[x+2][y-1]==0:
        return [1, x+2, y-1]
    elif position==7 and x+2<=Size.X.value-1 and y+1<=Size.X.value-1 and chess[x+2][y+1]==0:
        return [1, x+2, y+1]
    else:
        return [0, x, y]

def TravelChessBoard(x, y, tag):
    global chess
    chess[x][y] = tag
    if tag == Size.X.value**2:
        for i in chess:
            print(i)
        return "OK"
    f = 0
    for i in range(8):
        flag = nextXY(x, y, i)
        if flag[0]:
            statues = TravelChessBoard(flag[1], flag[2], tag+1)
            if statues=="OK":
                return "OK"
            f += 1
        else:
            f += 1
    if f == 8:
        chess[x][y] = 0

print(TravelChessBoard(2, 0, 1))
print(datetime.datetime.now() - start)

整单代码一共可以分为三个部分：变量准备部分，位置判断部分，循环递归部分。

1.变量准备部分：

• • 定义了一个size枚举类，这是用于实现C语言中宏定义的功能特意定义的，当然你用别的方法也行，主要就是为了方便改变棋盘的规模。
  • 定义了一个棋盘变量，是一个二维矩阵，全部元素初始化为0。也就是问题中的棋盘

2.位置判断部分：

• • 函数有三个参数，分别是坐标x, y和位置position， 这个位置position先来解释一下，如下图[1]所示，在国际象棋中，按照马的走法（马走日）对于任何一个位置，马能走的地方一共有8个位置，每一个位置对应的坐标变换不一样，这里的position对应的就是8种坐标变换方式。（x, y）就是马当前所处的位置坐标
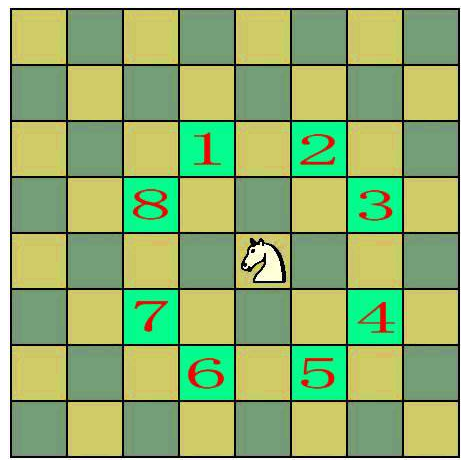
  • 返回的参数为一个列表，列表中包含三个元素，第一个元素表示8个位置是否存在满足条件的下一个位置，若存在，则第二、三两个元素返回新位置的坐标，若不存在，返回原始坐标
  • 判断的条件主要就是同时满足两个方面：坐标不能出界，坐标对应的位置未曾走过（位置上的值为0），两者都满足即存在满足条件的下一个位置
• 循环递归函数：

 def TravelChessBoard(x, y, tag):
     global chess
     chess[x][y] = tag
     if tag == Size.X.value**2:
         for i in chess:
             print(i)
         return "OK"
     f = 0
     for i in range(8):
         flag = nextXY(x, y, i)
         if flag[0]:
             statues = TravelChessBoard(flag[1], flag[2], tag+1)
             if statues=="OK":
                 return "OK"
             f += 1
         else:
             f += 1
     if f == 8:
         chess[x][y] = 0

• • 传进来的参数为当前马所在的位置（x, y），以及当前走的是第几步（tag的值）
  • 第行，chess[x][y] = tag， 另当前位置的值等于当前的步数，未到达的地方则为0，以此判断一个位置是否到达过
  • 第4-6行，如果步数等于棋盘的总格数（这里默认为方盘），则将棋盘打印出来，返回”OK“状态，告诉上一层递归已经寻找到解了，无需再作其它搜索了
  • 第行，定义一个过程变量f = 0， 作用稍后会讲到
  • 第-17行，对马的当前位置的下8个位置进行遍历，对于每一个位置，如果存在下个符合条件的位置则进入递归，将符合条件的下一个位置作为当前位置传入递归函数中，步数加1。对8个位置遍历，每次出现一个不符合条件的位置则f的值就加一。
  • 第18-19行，当8个位置全部遍历完，没有一个符合条件的位置，那么此时f = 8，说明当前位置是不符合条件，那么就将当前位置的值重新置为0。
  • 再说第12-15行，当深层的遍历找不到合适的位置时，递归会退回到前一层，这说明前一层的当前位置也不符合条件，那么f的值就必须加1，然后继续遍历前一层的下一个位置，以此类推。
  • 最后再说13-14行，当已经找到并打印出符合条件的路径后，程序饭后”OK“状态，此时程序的递归就会从最后一层不断往前一层返回，为了加快程序结束的速度，就不继续进行剩下的遍历，每一层递归都直接返回可以了。如果不直接返回的话，程序会将所有的情况都遍历完再返回，这样时间就会非常非常非常长。YOU CAN HAVE A TRY !!!

到此这个程序也差不多讲完了，我觉得只要理解递归了，这个程序应该不难理解。

---

连续几天都在用递归，对递归的运用也越来越熟练，确实非常好用，真诚地希望这篇文章对你有帮助。

愿各位学业有成！！！

[1] 图拷贝自http://blog.fishc.com/2554.html，感谢鱼C工作室。