数据结构实验6：C++实现二叉树类
实验6
学号： 姓名： 专业：
6.1 实验目的
掌握二叉树的动态链表存储结构及表示。
掌握二叉树的三种遍历算法（递归和非递归两类）。
运用二叉树三种遍历的方法求解有关问题。
6.2 实验要求
按照C++面向对象方法编写二叉树类；二叉树的测试数据可用多种方式进行输入，如键盘输入、静态写入、文件读入等。//最难的是从文件把数据读进去！
设计二叉树的二叉链表存储结构，编写算法实现下列问题的求解。
<1>打印出二叉树的三种遍历序列。
<2>设计算法按中序次序输出二叉树中各结点的值及其所对应的层次数。
<3>求二叉树的高度。
<4>求二叉树的结点数。
<5>求二叉树的叶子结点数。
<6>求二叉树的度为2的结点数。
<7>键盘输入一个元素x，求其父节点、兄弟结点、子结点的值，不存在时给出相应提示信息。对兄弟结点和孩子结点，存在时要明确指出是左兄弟、左孩子、右兄弟或右孩子。
<8>键盘输入一个元素x，求其在树中的层次，不存在时给出相应提示信息。
<9>将按顺序方式存储在数组中的二叉树转换为二叉链表形式。（数组中要扩展为完全二叉树）。
<10>交换二叉树中每个结点的左右孩子指针的值。（即：左子树变为右子树，右子树变为左子树）。
（下面为选做实验，有兴趣的同学完成）
<11>复制一棵二叉树T到T1。
<12>输出二叉树从每个叶子结点到根结点的路径（经历的结点）。
<13>对二叉链表表示的二叉树，按从上到下，从左到右打印结点值，即按层次打印。（提示：需要使用队列）
<14>对二叉链表表示的二叉树，求2个结点最近的共同祖先。
实验测试数据基本要求：
<15>求二叉树中一条最长的路径长度（边数），并输出路径上的个结点值。
实验测试数据基本要求：
6.3 实验数据要求
自我编写测试样例，要求每个功能函数的测试样例不少于两组
6.4 运行结果截图及说明
图1 测试（1）、（2）、（3）、（4）、（5）、（6）
图2 测试（1）、（2）、（3）、（4）、（5）、（6）
图3 测试（1）、（2）、（3）、（4）、（5）、（6）
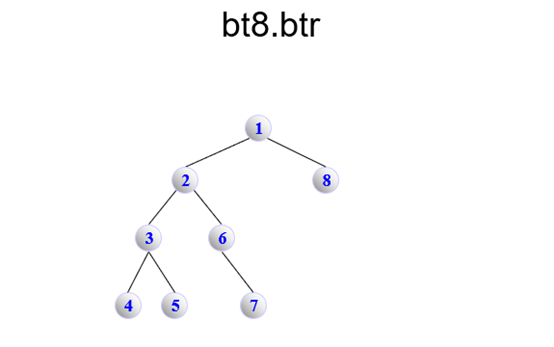
图4 测试（1）、（2）、（3）、（4）、（5）、（6）
图5 测试（1）、（2）、（3）、（4）、（5）、（6）
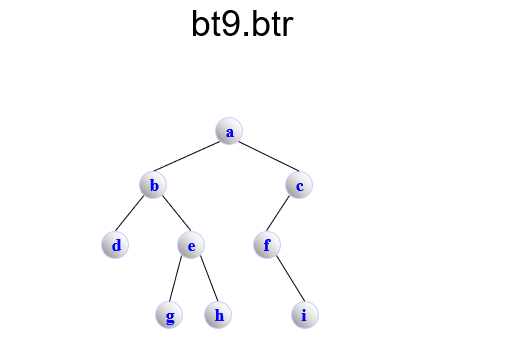
图6 测试（1）、（2）、（3）、（4）、（5）、（6）
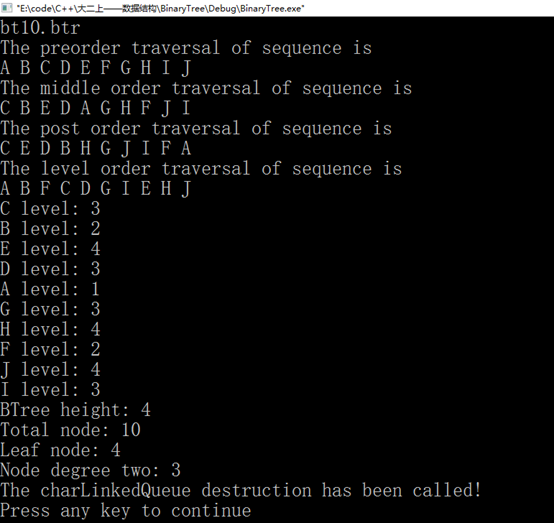
图7 测试（1）、（2）、（3）、（4）、（5）、（6）
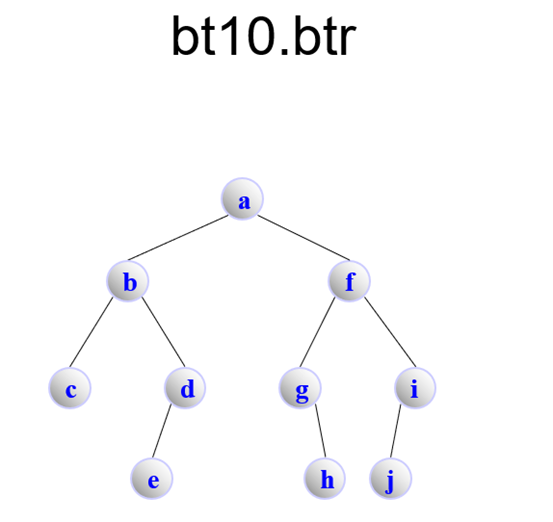
图8 测试（1）、（2）、（3）、（4）、（5）、（6）
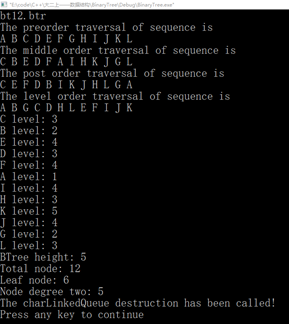
图9 测试（1）、（2）、（3）、（4）、（5）、（6）
图10 测试（1）、（2）、（3）、（4）、（5）、（6）
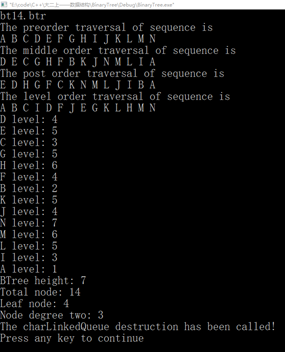
图11 测试（1）、（2）、（3）、（4）、（5）、（6）
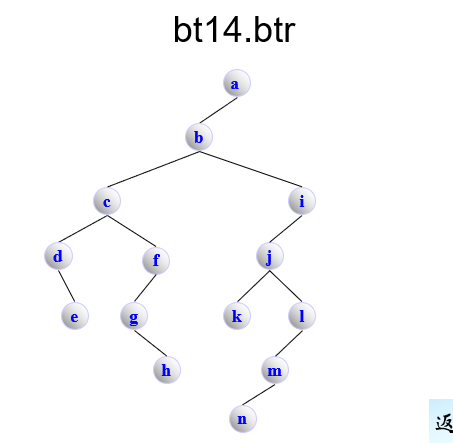
图12 测试（1）、（2）、（3）、（4）、（5）、（6）
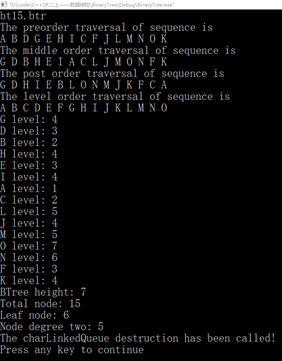
图13 测试（1）、（2）、（3）、（4）、（5）、（6）
图14 测试（1）、（2）、（3）、（4）、（5）、（6）
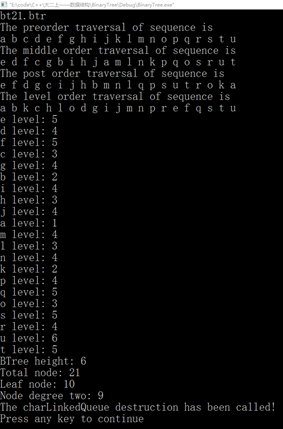
图15 测试（1）、（2）、（3）、（4）、（5）、（6）
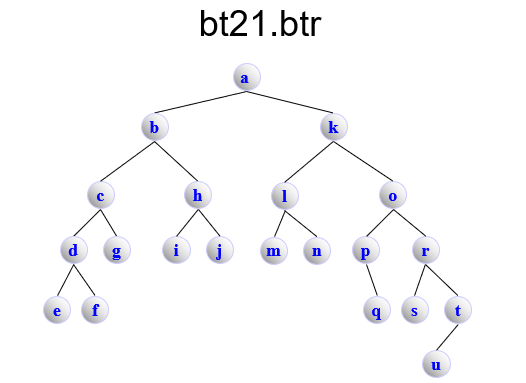
图16 测试（1）、（2）、（3）、（4）、（5）、（6）
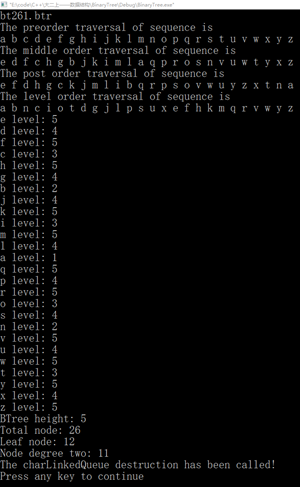
图17 测试（1）、（2）、（3）、（4）、（5）、（6）
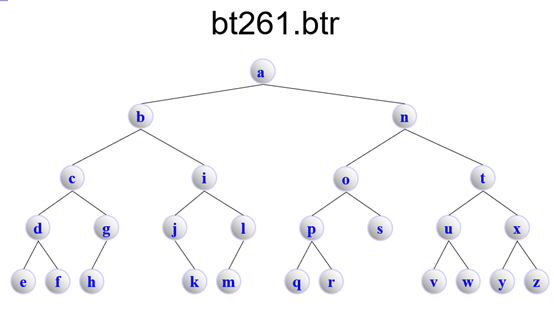
图18 测试（1）、（2）、（3）、（4）、（5）、（6）
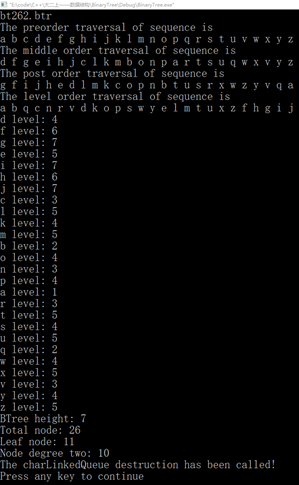
图19 测试（1）、（2）、（3）、（4）、（5）、（6）
图20 测试（1）、（2）、（3）、（4）、（5）、（6）
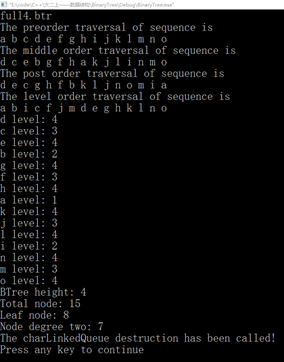
图21 测试（1）、（2）、（3）、（4）、（5）、（6）
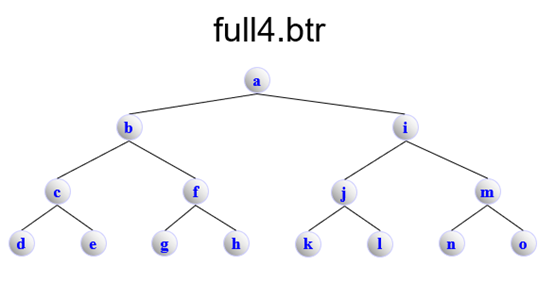
图22 测试（1）、（2）、（3）、（4）、（5）、（6）
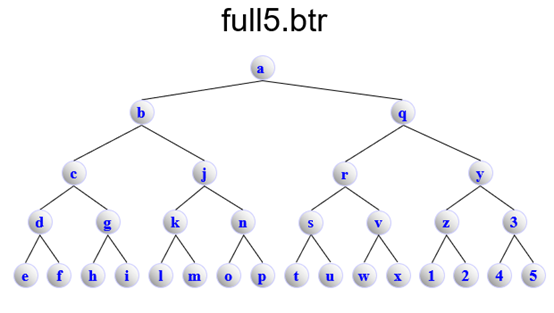
图23 测试（1）、（2）、（3）、（4）、（5）、（6）
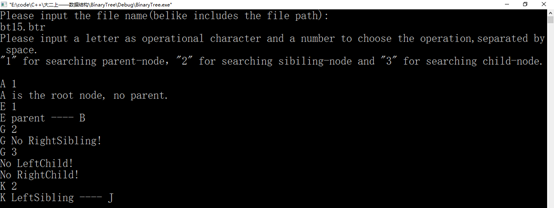
图24 测试（7）
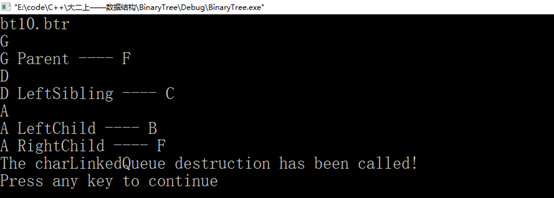
图25 测试（7）
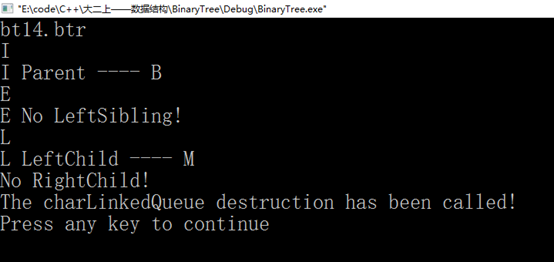
图26 测试（7）
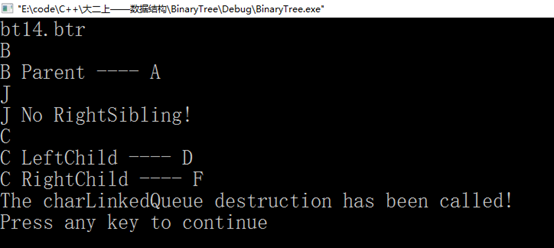
图27 测试（7）
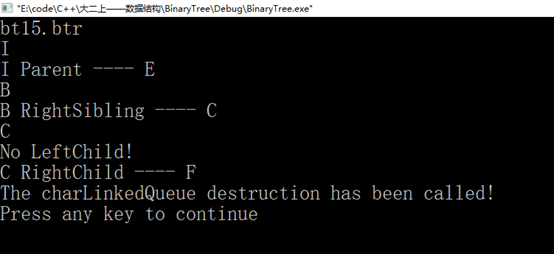
图28 测试（7）
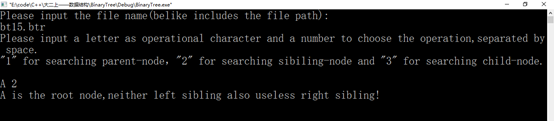
图29 测试（7）
图30 测试（7）
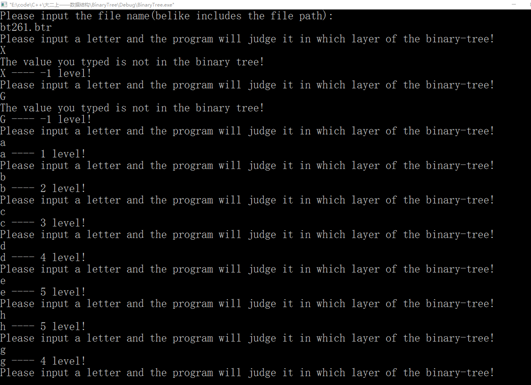
图31 测试（8）
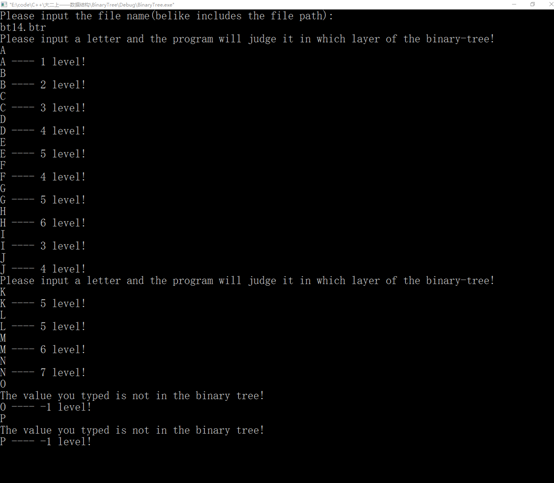
图32 测试（8）
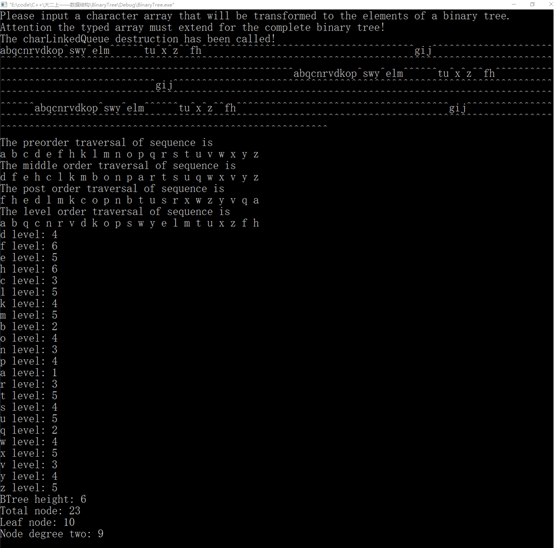
图33 测试（9）
图34 测试（9）
图35 测试（10）
图36 测试（10）
图37 测试（11）
图38 测试（11）
图39 测试（12）
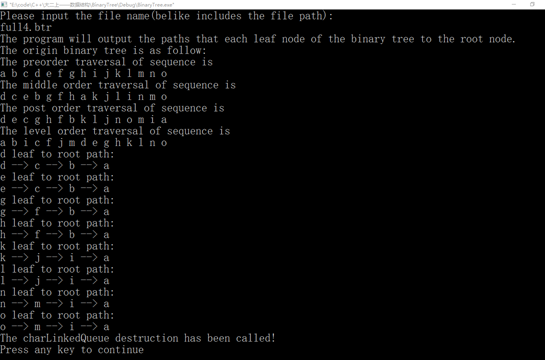
图40 测试（12）
图41 测试（13）
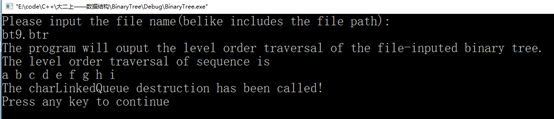
图42 测试（13）
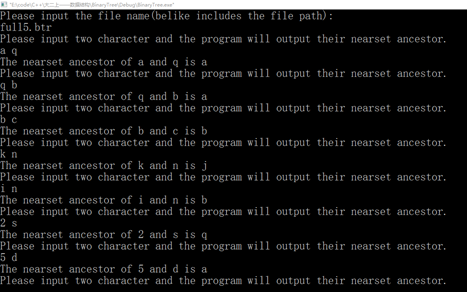
图43 测试（14）
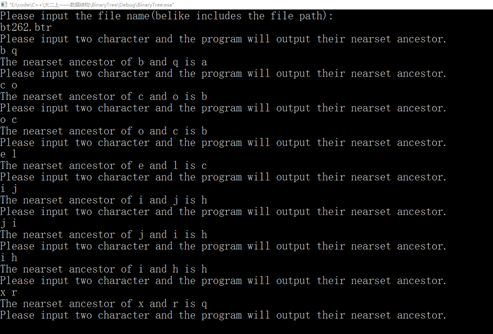
图44 测试（14）
图45 测试（15）
图46 测试（15）
6.5 附源代码
// stdafx.h : include file for standard system include files,
// or project specific include files that are used frequently, but
// are changed infrequently
// #if !defined(AFX_STDAFX_H__02F8C78B_9F6E_45FF_BFCE_7F99B5AC9359__INCLUDED_)
#define AFX_STDAFX_H__02F8C78B_9F6E_45FF_BFCE_7F99B5AC9359__INCLUDED_ #if _MSC_VER > 1000
#pragma once
#endif // _MSC_VER > 1000 #include <stdc++.h>
#include <windows.h> using namespace std; typedef char elementType;
typedef int elementType1; typedef struct node
{
elementType data;//刚开始应该写成将data写成string或者直接将整个函数写成模板的，写完了最后测试时
//才发现现在的写法有诸多不便；但修改的话就又要重构一遍，懒得整了。
struct node *leftChild, *rightChild;
}bitNode, *binTree; typedef struct charNode
{
//elementType data;
bitNode *data;//the type must be bitNode*
struct charNode *link;
}CLNode, *CPNode; //typedef struct charNode
//{
//elementType data;
//struct charNode *leftChild, *rightChild;
//}charBitNode, *charBinTree; // TODO: reference additional headers your program requires here //{{AFX_INSERT_LOCATION}}
// Microsoft Visual C++ will insert additional declarations immediately before the previous line. #endif // !defined(AFX_STDAFX_H__02F8C78B_9F6E_45FF_BFCE_7F99B5AC9359__INCLUDED_)
// charLinkedQueue.h: interface for the charLinkedQueue class.
//
////////////////////////////////////////////////////////////////////// #if !defined(AFX_CHARLINKEDQUEUE_H__13C2F642_81C0_4489_9CF2_3D58D8B48EA9__INCLUDED_)
#define AFX_CHARLINKEDQUEUE_H__13C2F642_81C0_4489_9CF2_3D58D8B48EA9__INCLUDED_ #if _MSC_VER > 1000
#pragma once
#endif // _MSC_VER > 1000 //刚开始尝试写英文注释的，后面知难而退了；不过原来的英文注释我保留了 class charLinkedQueue
{
public:
charLinkedQueue();
virtual ~charLinkedQueue();
bool emptyCharLinkedQueue();
//bool fullSeqCircleQueue();
bool enQueue( bitNode *value );//the type must be bitNode*
bool deQueue( /*bitNode *value*/ );
bool getFront( bitNode *&value );//the type must be bitNode*&
int length();
friend ostream &operator<<( ostream &os, charLinkedQueue &clq )
{
/*
if( ( scq._front - 1 ) % maxn == scq._rear )
return os;
int column = 0;
for( int i = scq._front; i % maxn != scq._rear; i = ( i + 1 ) % maxn )
{
os << setw(3) << setiosflags(ios::left) << scq.data[i] << " ";
column ++;
if( column % 10 == 0 )
os << endl;
}
os << endl;
*/
if( clq._front == NULL )
return os;
CLNode *tmp = clq._front;
int column = ;
while( tmp != clq._rear->link )
{
os << setw() << setiosflags(ios::left) << tmp->data << " ";
column ++;
tmp = tmp->link;
if( column % == )
os << endl;
}
os << endl;
}
//为了能顺利使用原来的这个代码块来进行二叉树的层次便利，我主要的精力都放在_front、_rear类型、
//deQueue()、enQueue()、charNode的类型确定上，经过无数次尝试，总算结果对了----
//如果有Git，看了这个代码的每个版本你就会知道我付出了多少心血。。。。
private:
CLNode *_front;//the type must be CLNode*
CLNode *_rear;//the type must be CLNode*
}; #endif // !defined(AFX_CHARLINKEDQUEUE_H__13C2F642_81C0_4489_9CF2_3D58D8B48EA9__INCLUDED_)
// _Binary_Tree.h: interface for the _Binary_Tree class.
//
////////////////////////////////////////////////////////////////////// #if !defined(AFX__BINARY_TREE_H__9381B15F_E185_4489_9415_360A22C0A4E2__INCLUDED_)
#define AFX__BINARY_TREE_H__9381B15F_E185_4489_9415_360A22C0A4E2__INCLUDED_ #if _MSC_VER > 1000
#pragma once
#endif // _MSC_VER > 1000 #include "charLinkedQueue.h" //刚开始尝试写英文注释的，后面知难而退了；不过原来的英文注释我保留了 class _Binary_Tree
{
public:
_Binary_Tree();//不带参数的构造函数
_Binary_Tree( elementType *Arr );//带参数的构造函数
void build( elementType *Arr );//从数组建立二叉树，相当于初始化；不带参数的构造函数无法适用于这里
void createNode( binTree BT, elementType *Arr, int number );//根据从数组读到的数据先序递归建树
virtual ~_Binary_Tree();//析构函数
bool createBinaryTree( binTree &BT, elementType stringLine[][], int length, int &row );//根据文本数据
//先序构造二叉树
bool readFileToArray( elementType stringLine[][], int &length );//将文本数据读入二维数组中
bool emptyBinaryTree();//二叉树判空，仅适用于带参数构造函数建立的二叉树
bool _exit( binTree BT, elementType value );//判断节点数据是否在二叉树中
binTree getNodePoint();//返回根节点地址
binTree getNodePoint( binTree BT, elementType value );//返回value在二叉树中的地址
binTree getParent( binTree BT, elementType value );//返回value的父母
void PreOrderTraverse(binTree BT);//前序遍历
void InOrderTraverse(binTree BT);//中序遍历
void PostOrderTraverse(binTree BT);//后序遍历
void levelOrderTraverse(binTree BT);//层次遍历
void destroy( binTree BT );//销毁二叉树
void level( binTree BT, int number );//求二叉树中各个节点的层次
int height( binTree BT );//求二叉树高度
int numberOfBTreeNode( binTree BT );//返回二叉树节点总数
int numberOfBTreeLeafNode( binTree BT, int &number );//返回二叉树叶节点个数
void numberOfNodeDegreeTwo( binTree BT, int &number );//求二叉树中度为2的节点个数
//void family( binTree BT, elementType1 number );
void getParent( binTree BT, elementType value, bool &flag );//求value的父节点
void getSibling( binTree BT, elementType value, bool &flag );//when call the function, the parameter flag
//must be assigned for false
//求value的兄弟节点，法1；有一个bug
void getSibling( binTree BT, elementType value );//求value的兄弟节点，法2
void getChild( binTree BT, elementType value, bool &flag );//求value孩子节点
int levelJudge( binTree BT, elementType value, int &number, int level );//返回value节点的层次
void exchangeLeftAndRightSibling( binTree BT );//交换左右子树
void copyBTree( binTree BT1, binTree BT );//复制二叉树
charLinkedQueue clq;//包含
void allLeafToRootPath( binTree BT, elementType *path, int &pathLength );//求所有叶节点到根节点路径
void binaryTreeLongestPath( binTree BT, elementType *path, int &pathLength,
elementType *longestPath, int &longestLength );//求叶节点到根节点的最长路径
binTree nearestAncestor( binTree BT, bitNode *BNode1, bitNode *BNode2 );//求两个节点的最近祖先
//本来打算用elementType数据
//作为参数的，后面发现行不通
//可能是我太菜了吧
private:
bitNode *BTree; }; #endif // !defined(AFX__BINARY_TREE_H__9381B15F_E185_4489_9415_360A22C0A4E2__INCLUDED_)
// charLinkedQueue.cpp: implementation of the charLinkedQueue class.
//
////////////////////////////////////////////////////////////////////// #include "stdafx.h"
#include "charLinkedQueue.h" //////////////////////////////////////////////////////////////////////
// Construction/Destruction
////////////////////////////////////////////////////////////////////// charLinkedQueue::charLinkedQueue()
{
_front = _rear = NULL;
} charLinkedQueue::~charLinkedQueue()
{
CLNode *tmp = NULL;
while( _front != _rear )
{
tmp = _front;
_front = _front->link;
delete tmp;
}
cout << "The charLinkedQueue destruction has been called!" << endl;
} bool charLinkedQueue::emptyCharLinkedQueue()
{
return _front == NULL;
} bool charLinkedQueue::enQueue( bitNode *value )
{
CLNode *newNode = new CLNode;
if( !newNode )
{
cerr << "Space allocating falied!Error in charLinkedQueue::enQueue()!" << endl;
return false;
}
newNode->data = value;
newNode->link = NULL;
if( emptyCharLinkedQueue() )
{
_front = _rear = newNode;
}
else
{
_rear->link = newNode;
_rear = newNode;
}
return true;
} bool charLinkedQueue::deQueue( /*elementType &value*/ )
{
if( emptyCharLinkedQueue() )
{
cerr << "Node deleting falied!Error in charLinkedQueue::deQueue()!" << endl;
return false;
}
CLNode *tmp = _front;
//value = _front->data;
_front = _front->link;
delete tmp;
if( _front == NULL )
_rear = NULL;
return true;
} bool charLinkedQueue::getFront( bitNode *&value )
{
if( emptyCharLinkedQueue() )
{
cerr << "Queue is empty!\nNode-data acquiring falied!Error in charLinkedQueue::deQueue()!" << endl;
return false;
}
value = _front->data;//原来我是注释掉的，导致输出一直是A；
return true;
} int charLinkedQueue::length()
{
if( emptyCharLinkedQueue() )
{
cerr << "Queue is empty!" << endl;
return -;
}
CLNode *tmp = _front;
int _size = ;
while( tmp != NULL )
{
tmp = tmp->link;
_size ++;
}
return _size;
}
// _Binary_Tree.cpp: implementation of the _Binary_Tree class.
//
////////////////////////////////////////////////////////////////////// #include "stdafx.h"
#include "_Binary_Tree.h"
#include "charLinkedQueue.h" //////////////////////////////////////////////////////////////////////
// Construction/Destruction
////////////////////////////////////////////////////////////////////// _Binary_Tree::_Binary_Tree() //新建一个结点
{
//BTree = NULL;
BTree = new bitNode;
BTree->leftChild = BTree->rightChild = NULL;
} _Binary_Tree::~_Binary_Tree()
{
destroy(BTree);//析构函数不能带参数，只能这么处理了
} _Binary_Tree::_Binary_Tree( elementType *Arr )
{
BTree = NULL;
build(Arr);
} void _Binary_Tree::build( elementType *Arr )
{
if(BTree)
destroy(BTree);
if( Arr[] == '^' )
{
BTree = NULL;
return;
}
BTree = new bitNode;
BTree->leftChild = NULL;
BTree->rightChild = NULL;
BTree->data = Arr[];
createNode( BTree, Arr, );
} void _Binary_Tree::createNode( binTree BT, elementType *Arr, int number )
{
bitNode *tmp = new bitNode;
if( Arr[ number * + ] != '^' )
{
BT->leftChild =new bitNode ;
tmp = BT->leftChild;
tmp->data = Arr[ number * + ];
tmp->leftChild = NULL;
tmp->rightChild = NULL;
createNode( tmp, Arr, number * + );
}
if( Arr[ number * + ] != '^' )
{
BT->rightChild =new bitNode ;
tmp = BT->rightChild;
tmp->data = Arr[ number * + ];
tmp->leftChild = NULL;
tmp->rightChild = NULL;
createNode( tmp, Arr, number * + );
}
} bool _Binary_Tree::createBinaryTree( binTree &BT, elementType stringLine[][], int length, int &row )
{
if (row >= length || length == ) //strlen存数据的二维数组，nRow结点所在的位数，nlen结点的个数
return false;
if ( row == )
BT = BTree;
else
BT = new bitNode;//new下面是公用的，用if的目的是改变private里BTree里的值
BT->data = stringLine[row][];
BT->leftChild = NULL;
BT->rightChild = NULL; int nextRow = row;
if ( stringLine[nextRow][] == '' )
{
++ row;
createBinaryTree( BT->leftChild, stringLine, length, row );
}
if ( stringLine[nextRow][] == '' )
{
++row;
createBinaryTree( BT->rightChild, stringLine, length, row );
}
return true;
} bool _Binary_Tree::readFileToArray( elementType stringLine[][], int &length )
{
FILE *fp;
char str[]; cout << "Please input the file name(belike includes the file path):" << endl;
char name[];// = "bt10.btr";
cin >> name;
fp = fopen( name, "r" );
if (!fp)
{
cout << "Error!" << endl;
return false;
}
if (fgets(str, , fp) != NULL)
{
if (strcmp(str, "BinaryTree\n") != )
{
cout << "Error!" << endl;
fclose(fp);
return false;
}
}
length = ;
while (fscanf(fp, "%c %c %c\n", &stringLine[length][], &stringLine[length][], &stringLine[length][]) != EOF)
{
length ++;
}
fclose(fp);
return true;
} bool _Binary_Tree::emptyBinaryTree()
{
//if(BTree)
//return BTree->leftChild == NULL && BTree->rightChild == NULL;
//else
return BTree == NULL;
} bool _Binary_Tree::_exit( binTree BT, elementType value )
{
if(!BT)
return false;
//return NULL;
if( BT->data == value )
return true;
//return BT;
//bitNode *index = _exit( BT->leftChild, value );
bool flag = _exit( BT->leftChild, value );
//if(!index)
if(!flag)
//_exit( BT->leftChild, value );
_exit( BT->rightChild, value );
} binTree _Binary_Tree::getNodePoint()
{
//if( emptyBinaryTree() )
//{
//throw "Empty binary tree!Error in binTree _Binary_Tree::getNodePoint()!\n";
//return NULL;
//}
return (*this).BTree;
} binTree _Binary_Tree::getNodePoint( binTree BT, elementType value )
{
/*
if(!BT)
{
return NULL;
}
else
{
if( BT->data == value )
return BT;
else
{
bitNode *tmp;
if( tmp = getNodePoint( BT->leftChild, value ) )
return tmp;
if( tmp = getNodePoint( BT->rightChild, value ) )
return tmp;
return NULL;
}
}
*/
if(!BT)
{
return NULL;
}
else
{
if( BT->data == value )
{
return BT;
}
//getNodePoint( BT->leftChild, value );
//getNodePoint( BT->rightChild, value ); bitNode *tmp = getNodePoint( BT->leftChild, value );
if(!tmp)
{
getNodePoint( BT->rightChild, value );
}
//follow statement can't be added to the code
//return tmp;
}
} void _Binary_Tree::PreOrderTraverse(binTree BT)
{
//if( emptyBinaryTree() )
// {
//throw "Empty binary tree!Error in void _Binary_Tree::PreOrderTraverse(binTree BT) !\n";
//return;
//}
if (BT)
{
cout << BT->data << " ";
PreOrderTraverse(BT->leftChild);
PreOrderTraverse(BT->rightChild);
}
} void _Binary_Tree::InOrderTraverse(binTree BT)
{
if (BT)
{
InOrderTraverse(BT->leftChild);
cout << BT->data << " ";
InOrderTraverse(BT->rightChild);
}
//return 0;
} void _Binary_Tree::PostOrderTraverse( binTree BT )
{
if (BT)
{
PostOrderTraverse(BT->leftChild);
PostOrderTraverse(BT->rightChild);
cout << BT->data << " ";
}
} void _Binary_Tree::destroy( binTree BT )
{
if(BT)
{
destroy( BT->leftChild );
destroy( BT->rightChild );
delete BT;
BT = NULL;
}
} void _Binary_Tree::level( binTree BT, int number )
{ if(BT)
{
level( BT->leftChild, number + );
///number +=3;
//cout << number << endl;
cout << BT->data << " level: " << number << endl; level( BT->rightChild, number + );
//number -=2;
}
//number --;
} int _Binary_Tree::height( binTree BT )
{
if(!BT)
{
return ;
}
else
{
int i = height( BT->leftChild );
int j = height( BT->rightChild );
return i < j ? j + : i + ; }
} int _Binary_Tree::numberOfBTreeNode( binTree BT )
{
if(!BT)
return ;
else
{
return numberOfBTreeNode( BT->leftChild ) + numberOfBTreeNode( BT->rightChild ) + ;
}
} int _Binary_Tree::numberOfBTreeLeafNode( binTree BT, int &number )
{
if(!BT)
{
return ;
}
else
{
if( !BT->leftChild && !BT->rightChild )
//number += 1;
number ++;
//return 1;
else
{
numberOfBTreeLeafNode( BT->leftChild, number );
numberOfBTreeLeafNode( BT->rightChild, number );
}
return number;
}
} void _Binary_Tree::numberOfNodeDegreeTwo( binTree BT, int &number )
{
if(!BT)
{
return;
}
else
{
if( BT->leftChild && BT->rightChild )
//number += 1;
number += ;
//return 1;
//else
//{
numberOfNodeDegreeTwo( BT->leftChild, number );
numberOfNodeDegreeTwo( BT->rightChild, number );
//return numberOfNodeDegreeTwo( BT->leftChild, number ) + numberOfNodeDegreeTwo( BT->rightChild, number );
//}
//return number;
}
} /*
void _Binary_Tree::family( binTree BT, elementType1 number )
{
if(!BT)
{
return;
}
if( BT->leftChild->data == number || BT->rightChild->data == number )
{
cout << "parent ---- " << BT->data << endl;
if( BT->leftChild->data == number && BT->rightChild )
{
cout << "rights sibling ---- " << BT->rightChild->data << endl;
}
if( BT->leftChild && BT->rightChild->data == number )
{
cout << "left sibling ---- " << BT->leftChild->data << endl;
}
}
if( BT->data == number && ( BT->leftChild || BT->rightChild ) )
{
cout << ( BT->leftChild ? "left child ---- " : true ) << endl;
cout << ( BT->rightChild ? "right child ---- " : true ) << endl;
}
family( BT->leftChild, number );
family( BT->rightChild, number );
//if( BT->data == number && BT-)
//if( BT->leftChild->data == number &&)
}
*/ //bool _Binary_Tree::getParent( binTree BT, elementType number, bool flag )
void _Binary_Tree::getParent( binTree BT, elementType value, bool &flag )
{
if(!BT)
{
//return false;
return;
}
if( ( BT->leftChild && BT->leftChild->data == value ) || ( BT->rightChild ) && ( BT->rightChild->data == value ) )
{
flag = true;
cout << value << " Parent ---- " << BT->data << endl;
return;
//return true;
}
/*
if( BT && BT->rightChild->data == number )
{
cout << "parent ---- " << BT->data << endl;
return true;
}
*/
getParent( BT->leftChild, value, flag );
getParent( BT->rightChild, value, flag );
} binTree _Binary_Tree::getParent( binTree BT, elementType value )
{ if( !_exit( BT, value ) )
{
cerr << value << " is not in the binary tree!" << endl;
cerr << "Error in binTree _Binary_Tree::getParent( binTree BT, elementType value )!" << endl;
return NULL;
} if(!BT)
{
return NULL;
}
if( BT->data == value )
{
return BT;
}
if( ( BT->leftChild && BT->leftChild->data == value ) || ( BT->rightChild && BT->rightChild->data == value ) )//|| BT->rightChild->data == value )
{
return BT;
}
bitNode *tmp = getParent( BT->leftChild, value );
if(!tmp)
{
getParent( BT->rightChild, value );
}
} void _Binary_Tree::getSibling( binTree BT, elementType value, bool &flag )
{
if(!BT)
{
cout << value << " No LeftSibling!" << endl << value << " No RightSibling!" << endl;
return;
}
if( !flag && !BT->leftChild )//|| !BT->rightChild )//write as "if(!BT)" would result error
{ if( BT->rightChild )
{
getSibling( BT->rightChild, value, flag );
//return;
}
else
{
//cout << value << " No LeftSibling!" << endl;
return;
}
return;//why would deleting the statement cause error!
} if( !flag && !BT->rightChild )
{ if( BT->leftChild )
{
getSibling( BT->leftChild, value, flag ); }
else
{
//cout << value << "No LeftSibling!" << endl;
//cout << value << " No RightSibling!" << endl;
return; }
return;//why would deleting the statement cause error!
}
if( BT->rightChild->data == value )
{
if( BT->leftChild )
{
flag = true;
cout << value << " LeftSibling ---- " << BT->leftChild->data << endl;
return;
}
else if( !BT->leftChild )
{
cout << value << " No LeftSibling!" << endl;
return;
} }
if( BT->leftChild->data == value )
{
if( BT->rightChild )
{
flag = true;
cout << value << " RightSibling ---- " << BT->rightChild->data << endl;
return;
}
else if( !BT->rightChild )
{
cout << value << " No RightSibling!" << endl;
return;
}
}
getSibling( BT->leftChild, value, flag );
if( !flag && BT->rightChild )
getSibling( BT->rightChild, value, flag );
} void _Binary_Tree::getSibling( binTree BT, elementType value )
{
bitNode *parent = getParent( BT, value ); if( BT->data == value )
{
cout << value << " is the root node,neither left sibling also useless right sibling!" << endl;
return;
}
if( !_exit( BT, value ) )
{
cout << value << " is not in the binary-tree!" << endl;
cerr << "Error in void _Binary_Tree::getSibling( binTree BT, elementType value )!" << endl;
return;
}
if( parent->leftChild && parent->leftChild->data == value )
{
if( parent->rightChild )
{
cout << value << " RightSibling ---- " << parent->rightChild->data << endl;
return;
}
else
{
cout << value << " No RightSibling!" << endl;
return;
}
}
if( parent->rightChild && parent->rightChild->data == value )
{
if( parent->leftChild )
{
cout << value << " LeftSibling ---- " << parent->leftChild->data << endl;
return;
}
else
{
cout << value << " No LeftSibling!" << endl;
return;
}
}
} void _Binary_Tree::getChild( binTree BT, elementType value, bool &flag )//It costed me several minutes to
{ //write and almost one hour to
/* //perfect the function
if( BT->leftChild )
{
getChild( BT->leftChild, value, flag );
}
if( BT->rightChild )
{
getChild( BT->rightChild, value, flag );
}
*/ /*
if( !BT->leftChild )//|| !BT->rightChild )
{
if(flag)
{
cout << "No LeftChild! " << endl;
flag = true;
return;
}
else
{
cout << "No LeftChild! " << endl;
flag = false;
}
//return;
}
if( !BT->rightChild )
{
if(flag)
{
cout << "No RightChild! " << endl;
flag = true;
return;
}
else
{
cout << "No RightChild! " << endl;
flag = false;
}
}
*/
//if(!BT)
// {
// return;
// }
if( !_exit( BT, value ) )
{
cerr << value << " is not in the binary tree!\nError in void _Binary_Tree::getChild( binTree BT, elementType value, bool &flag )" << endl;
return;
}
if( BT->data == value )//at first I neglected this detail that resulted wrong judgement at root-node
{
if( BT->leftChild )
{
flag = true;
cout << value << " LeftChild ---- " << BT->leftChild->data << endl; }
else
{
cout << "No LeftChild!" << endl; }
if( BT->rightChild )
{
flag = true;
cout << value << " RightChild ---- " << BT->rightChild->data << endl;
return;
}
else
{
cout << "No RightChild! " << endl;
return;
}
}
if( !BT->leftChild )
{
if( BT->rightChild )
{
getChild( BT->rightChild, value, flag );
}
return;
/*
if(flag)
{
return;
}
else
{
flag = false;
return;
}*/
}
if( !BT->rightChild )
{
if( BT->leftChild )
{
getChild( BT->leftChild, value, flag );
}
return;
//if(flag)
//{
// flag = false;
//}
/*
if(flag)
{
return;
}
else
{
flag = false;
return;
}*/
}
/*
if( BT->rightChild->data == value )
{
if( BT->rightChild->leftChild )
{
flag = true;
cout << value << " LeftChild ---- " << BT->rightChild->leftChild->data << endl;
//return;
}
else
{
cout << "No LeftChild!" << endl;
}
if( BT->rightChild->rightChild )
{
flag = true;
cout << value << " RightChild ---- " << BT->rightChild->rightChild->data << endl;
return;
}
else
{
cout << "No RightChild! " << endl;
return;
}
//else
//{
//flag = false;
// return;
//}
}
if( BT->leftChild->data == value )
{
if( BT->leftChild->leftChild )
{
flag = true;
cout << value << " LeftChild ---- " << BT->leftChild->leftChild->data << endl;
//return;
}
else
{
cout << "No LeftChild!" << endl;
}
if( BT->leftChild->rightChild )
{
flag = true;
cout << value << " RightChild ---- " << BT->leftChild->rightChild->data << endl;
return;
}
else
{
cout << "No RightChild! " << endl;
return;
}
//else
//{
//flag = false;
// return;
//}
}
*/
getChild( BT->leftChild, value, flag );
getChild( BT->rightChild, value, flag );
} int _Binary_Tree::levelJudge( binTree BT, elementType value, int &number, int level )
{
bitNode *position = getNodePoint( getNodePoint(), value );
if(!position)
{
cout << "The value you typed is not in the binary tree!" << endl;
//return -1;
number = -;
return number;
}
/*
int level;
if ( BT == NULL )
return 0;
else if ( BT->data == value )
return number;
else
{
number ++;
level = levelJudge( BT->leftChild, value, number );
if ( level != 0 )
return number;
else
{
//number ++;
return levelJudge( BT->rightChild, value, number );
}
}
*/
if(BT)
{
if( BT->data == value )
{
//number ++;
number = level;
}
//number ++;
levelJudge( BT->leftChild, value, number, level + );
//number ++;
levelJudge( BT->rightChild, value, number, level + );
}
} void _Binary_Tree::exchangeLeftAndRightSibling( binTree BT )
{
if( BT && BT->leftChild && BT->rightChild )
{
bitNode *tmp = BT->leftChild;
BT->leftChild = BT->rightChild;
BT->rightChild = tmp;
exchangeLeftAndRightSibling( BT->leftChild );
exchangeLeftAndRightSibling( BT->rightChild );
}
} void _Binary_Tree::copyBTree( binTree BT1, binTree BT )
{
bitNode *tmp = NULL;//new bitNode;
BT1->data = BT->data;
if( BT->leftChild )
{
BT1->leftChild = new bitNode;
tmp = BT1->leftChild;
tmp->leftChild = NULL;
tmp->rightChild = NULL;
copyBTree( tmp, BT->leftChild );
}
if( BT->rightChild )
{
BT1->rightChild = new bitNode;
tmp = BT1->rightChild;
tmp->leftChild = NULL;
tmp->rightChild = NULL;
copyBTree( tmp, BT->rightChild );
}
} void _Binary_Tree::levelOrderTraverse( binTree BT )
{
clq.enQueue(BT);
while( !clq.emptyCharLinkedQueue() )
{
//CLNode *tmp = NULL;
clq.getFront(BT);
cout << BT->data << " ";
clq.deQueue();
if( BT->leftChild != NULL )
{
clq.enQueue( BT->leftChild );
}
if( BT->rightChild != NULL )
{
clq.enQueue( BT->rightChild );
}
}
} void _Binary_Tree::allLeafToRootPath( binTree BT, char *path, int &pathLength )
{
if(BT)
{
if( !BT->leftChild && !BT->rightChild )
{
path[pathLength] = BT->data;
cout << BT->data << " leaf to root path: " << endl;
for( int i = pathLength; i >= ; i -- )
{
if( i != )
cout << path[i] << " --> ";
else
cout << path[i] << "\n";
}
//cout << endl;
}
else
{
path[ pathLength ++ ] = BT->data;
allLeafToRootPath( BT->leftChild, path, pathLength );
allLeafToRootPath( BT->rightChild, path, pathLength );
pathLength --;
}
}
} void _Binary_Tree::binaryTreeLongestPath( binTree BT, elementType *path, int &pathLength,
elementType *longestPath, int &longestLength )
{
if(BT)
{
if( !BT->leftChild && !BT->rightChild )
{
path[pathLength] = BT->data;
if( pathLength > longestLength)
{
//cout << BT->data << " leaf to root path: " << endl;
//longestPath = pathLength;
for( int i = pathLength; i >= ; i -- )
{
/*
if( i != 0 )
cout << path[i] << " --> ";
else
cout << path[i] << "\n";
*/
longestPath[i] = path[i];
}
longestLength = pathLength;
}
//longestLength = pathLength;
//cout << endl;
}
else
{
path[ pathLength ++ ] = BT->data;
binaryTreeLongestPath( BT->leftChild, path, pathLength, longestPath, longestLength );
binaryTreeLongestPath( BT->rightChild, path, pathLength, longestPath, longestLength );
pathLength --;
}
}
} binTree _Binary_Tree::nearestAncestor( binTree BT, bitNode *BNode1, bitNode *BNode2 )
{
// if( !_exit( BT, BNode1->data ) )
//{
// cout << BNode1->data << " is not in the binary tree!" << endl;
// return NULL;
//}
//if( !_exit( BT, BNode2->data ) )
//{
// cout << BNode2->data << " is not in the binary tree!" << endl;
// return NULL;
//}
if( !BT || !BNode1 || !BNode2 )
{
//cout << "NO ANCESTOR!" << endl;
return NULL;
}
if( BT == BNode1 || BT == BNode2 )
{
//cout << BT->data << endl;
return BT;
}
bitNode *left = nearestAncestor( BT->leftChild, BNode1, BNode2 );
bitNode *right = nearestAncestor( BT->rightChild, BNode1, BNode2 );
if( left && right )
{
//cout << BT->data << endl;
return BT;
}
else if(!left)
{
//cout << right->data << endl;
return right;
}
else
{
//cout << left->data << endl;
return left;
}
}
// BinaryTree.cpp : Defines the entry point for the console application.
// #include "stdafx.h"
#include "_Binary_Tree.h"
#include "charLinkedQueue.h" void test1()
{
_Binary_Tree BT1;
elementType strLine[][];
int nRow = , nLen = ;
binTree index;
BT1.readFileToArray(strLine,nLen);
//BT1._Binary_Tree(); BT1.createBinaryTree( index,strLine, nLen, nRow); cout << "The preorder traversal of sequence is" << endl;
BT1.PreOrderTraverse(BT1.getNodePoint());
cout << endl;
cout << "The middle order traversal of sequence is" << endl;
BT1.InOrderTraverse(BT1.getNodePoint());
cout << endl;
cout << "The post order traversal of sequence is" << endl;
BT1.PostOrderTraverse(BT1.getNodePoint());
cout << endl;
cout << "The level order traversal of sequence is" << endl;
BT1.levelOrderTraverse( BT1.getNodePoint() );
cout << endl;
int n = ;
BT1.level( BT1.getNodePoint() , n );
cout << "BTree height: "<< BT1.height( BT1.getNodePoint() ) << endl;
cout << "Total node: " << BT1.numberOfBTreeNode( BT1.getNodePoint() ) << endl;
int m = ;
cout << "Leaf node: " << BT1.numberOfBTreeLeafNode( BT1.getNodePoint(), m ) << endl;
int a = ;
BT1.numberOfNodeDegreeTwo( BT1.getNodePoint(), a );
cout << "Node degree two: " << a << endl;
} void test2()
{
_Binary_Tree BT1;
elementType strLine[][];
int nRow = , nLen = ;
binTree index;
BT1.readFileToArray(strLine,nLen);
//BT1._Binary_Tree(); BT1.createBinaryTree( index,strLine, nLen, nRow);
char ch;
int key;
cout << "Please input a letter as operational character and a number to choose the operation,separated by space.\n\"1\" for searching parent-node，\"2\" for searching sibiling-node and \"3\" for searching child-node." << endl;
while( cin>> ch >> key )
{
if( key == )
{
bool flag = false;
bitNode *index = NULL;
index = BT1.getParent( BT1.getNodePoint(), ch );
if( index && index != BT1.getNodePoint() )
cout << ch << " parent ---- " << index->data << endl;
else if( index && index->data == ch )
cout << ch << " is the root node, no parent." << endl;
else if(index)
cout << ch << " parent ---- " << index->data << endl;
}
else if( key == )
{
BT1.getSibling( BT1.getNodePoint(), ch );
}
else if( key == )
{
bool flag;
BT1.getChild( BT1.getNodePoint(), ch, flag );
}
//Sleep( 1000 * 60 );
//system( "cls" );
//cout << "Please input a letter as operational character and a number to choose the operation,separated by space.\n\"1\" for searching parent-node，\"2\" for searching sibiling-node and \"3\" for searching child-node." << endl;
}
} void test3()
{
_Binary_Tree BT1;
elementType strLine[][];
int nRow = , nLen = ;
binTree index;
BT1.readFileToArray(strLine,nLen);
//BT1._Binary_Tree(); BT1.createBinaryTree( index,strLine, nLen, nRow); elementType value;
int cnt = ;
cout << "Please input a letter and the program will judge it in which layer of the binary-tree!" << endl;
while( cin >> value )
{
int number = ;
BT1.levelJudge( BT1.getNodePoint(), value , number, );
cout << value << " ---- " << number << " level!" << endl;
cnt ++;
//Sleep( 1000 * 60 );
if( cnt % == )
system( "cls" ); cout << "Please input a letter and the program will judge it in which layer of the binary-tree!" << endl;
}
} void test4()
{
elementType str[];
cout << "Please input a character array that will be transformed to the elements of a binary tree.\nAttention the typed array must extend for the complete binary tree!" << endl;
while( cin >> str )
{
_Binary_Tree BT1(str);
cout << "The preorder traversal of sequence is" << endl;
BT1.PreOrderTraverse(BT1.getNodePoint());
cout << endl;
cout << "The middle order traversal of sequence is" << endl;
BT1.InOrderTraverse(BT1.getNodePoint());
cout << endl;
cout << "The post order traversal of sequence is" << endl;
BT1.PostOrderTraverse(BT1.getNodePoint());
cout << endl;
cout << "The level order traversal of sequence is" << endl;
BT1.levelOrderTraverse( BT1.getNodePoint() );
cout << endl;
int n = ;
BT1.level( BT1.getNodePoint() , n );
cout << "BTree height: "<< BT1.height( BT1.getNodePoint() ) << endl;
cout << "Total node: " << BT1.numberOfBTreeNode( BT1.getNodePoint() ) << endl;
int m = ;
cout << "Leaf node: " << BT1.numberOfBTreeLeafNode( BT1.getNodePoint(), m ) << endl;
int a = ;
BT1.numberOfNodeDegreeTwo( BT1.getNodePoint(), a );
cout << "Node degree two: " << a << endl;
Sleep( * );
system( "cls" );
cout << "Please input a character array that will be transformed to the elements of a binary tree.\nAttention the typed array must extend for the complete binary tree!" << endl;
}
} void test5()
{
_Binary_Tree BT1;
elementType strLine[][];
int nRow = , nLen = ;
binTree index;
BT1.readFileToArray(strLine,nLen);
//BT1._Binary_Tree(); BT1.createBinaryTree( index,strLine, nLen, nRow);
cout << "The program will exchange the left subtree and right subtree of the file-inputed binary tree!" << endl;
cout << "The origin binary tree is as follow:" << endl; cout << "The preorder traversal of sequence is" << endl;
BT1.PreOrderTraverse(BT1.getNodePoint());
cout << endl;
cout << "The middle order traversal of sequence is" << endl;
BT1.InOrderTraverse(BT1.getNodePoint());
cout << endl;
cout << "The post order traversal of sequence is" << endl;
BT1.PostOrderTraverse(BT1.getNodePoint());
cout << endl;
cout << "The level order traversal of sequence is" << endl;
BT1.levelOrderTraverse( BT1.getNodePoint() );
cout << endl; BT1.exchangeLeftAndRightSibling( BT1.getNodePoint() );
cout << "The following for the exchange of binary tree:" << endl;
cout << "The preorder traversal of sequence is" << endl;
BT1.PreOrderTraverse(BT1.getNodePoint());
cout << endl;
cout << "The middle order traversal of sequence is" << endl;
BT1.InOrderTraverse(BT1.getNodePoint());
cout << endl;
cout << "The post order traversal of sequence is" << endl;
BT1.PostOrderTraverse(BT1.getNodePoint());
cout << endl;
cout << "The level order traversal of sequence is" << endl;
BT1.levelOrderTraverse( BT1.getNodePoint() );
cout << endl;
} void test6()
{
_Binary_Tree BT1;
elementType strLine[][];
int nRow = , nLen = ;
binTree index;
BT1.readFileToArray(strLine,nLen);
//BT1._Binary_Tree(); BT1.createBinaryTree( index,strLine, nLen, nRow);
cout << "The program will copy the file-inputed binary tree to another empty one!" << endl;
_Binary_Tree BT2; cout << "The origin binary tree is as follow:" << endl;
cout << "The preorder traversal of sequence is" << endl;
BT1.PreOrderTraverse(BT1.getNodePoint());
cout << endl;
cout << "The middle order traversal of sequence is" << endl;
BT1.InOrderTraverse(BT1.getNodePoint());
cout << endl;
cout << "The post order traversal of sequence is" << endl;
BT1.PostOrderTraverse(BT1.getNodePoint());
cout << endl;
cout << "The level order traversal of sequence is" << endl;
BT1.levelOrderTraverse( BT1.getNodePoint() );
cout << endl; cout << "The empty binary tree is as follow:" << endl; cout << "The preorder traversal of sequence is" << endl;
BT2.PreOrderTraverse(BT2.getNodePoint());
cout << endl;
cout << "The middle order traversal of sequence is" << endl;
BT2.InOrderTraverse(BT2.getNodePoint());
cout << endl;
cout << "The post order traversal of sequence is" << endl;
BT2.PostOrderTraverse(BT2.getNodePoint());
cout << endl;
cout << "The level order traversal of sequence is" << endl;
BT2.levelOrderTraverse( BT2.getNodePoint() );
cout << endl; cout << "The following for the copy of binary tree:" << endl; BT1.copyBTree( BT2.getNodePoint(), BT1.getNodePoint() ); cout << "The preorder traversal of sequence is" << endl;
BT2.PreOrderTraverse(BT2.getNodePoint());
cout << endl;
cout << "The middle order traversal of sequence is" << endl;
BT2.InOrderTraverse(BT2.getNodePoint());
cout << endl;
cout << "The post order traversal of sequence is" << endl;
BT2.PostOrderTraverse(BT2.getNodePoint());
cout << endl;
cout << "The level order traversal of sequence is" << endl;
BT2.levelOrderTraverse( BT2.getNodePoint() );
cout << endl; } void test7()
{
_Binary_Tree BT1;
elementType strLine[][];
int nRow = , nLen = ;
binTree index;
BT1.readFileToArray(strLine,nLen);
//BT1._Binary_Tree(); BT1.createBinaryTree( index,strLine, nLen, nRow);
cout << "The program will output the paths that each leaf node of the binary tree to the root node." << endl; cout << "The origin binary tree is as follow:" << endl;
cout << "The preorder traversal of sequence is" << endl;
BT1.PreOrderTraverse(BT1.getNodePoint());
cout << endl;
cout << "The middle order traversal of sequence is" << endl;
BT1.InOrderTraverse(BT1.getNodePoint());
cout << endl;
cout << "The post order traversal of sequence is" << endl;
BT1.PostOrderTraverse(BT1.getNodePoint());
cout << endl;
cout << "The level order traversal of sequence is" << endl;
BT1.levelOrderTraverse( BT1.getNodePoint() );
cout << endl; int pathLength = ;
elementType *path = new char[ BT1.numberOfBTreeNode( BT1.getNodePoint() ) ];
BT1.allLeafToRootPath( BT1.getNodePoint(), path, pathLength ); } void test8()
{
_Binary_Tree BT1;
elementType strLine[][];
int nRow = , nLen = ;
binTree index;
BT1.readFileToArray(strLine,nLen);
//BT1._Binary_Tree(); BT1.createBinaryTree( index,strLine, nLen, nRow);
cout << "The program will ouput the level order traversal of the file-inputed binary tree." << endl;
cout << "The level order traversal of sequence is" << endl;
BT1.levelOrderTraverse( BT1.getNodePoint() );
cout << endl;
} void test9()
{
_Binary_Tree BT1;
char strLine[][];
int nRow = , nLen = ;
binTree index;
BT1.readFileToArray(strLine,nLen);
//BT1._Binary_Tree(); BT1.createBinaryTree( index,strLine, nLen, nRow); cout << "Please input two character and the program will output their nearset ancestor." << endl;
elementType ch1, ch2;
while( cin >> ch1 >> ch2 )
{
//BT1.nearestAncestor( binTree BT, bitNode *BNode1, bitNode *BNode2 );
bitNode *index1 = BT1.getNodePoint( BT1.getNodePoint(), ch1 ); if(!index1)
{
cout << ch1 << " is not in the binary tree!" << endl;
} bitNode *index2 = BT1.getNodePoint( BT1.getNodePoint(), ch2 ); if(!index2)
{
cout << ch2 << " is not in the binary tree!" << endl;
} if( index1 && index2 )
{
bitNode *target = BT1.nearestAncestor( BT1.getNodePoint(), index1, index2 );
cout << "The nearset ancestor of " << ch1 << " and " << ch2 << " is " << target->data << endl;
}
cout << "Please input two character and the program will output their nearset ancestor." << endl;
}
} void test10()
{
_Binary_Tree BT1;
char strLine[][];
int nRow = , nLen = ;
binTree index;
BT1.readFileToArray(strLine,nLen);
//BT1._Binary_Tree(); BT1.createBinaryTree( index,strLine, nLen, nRow);
cout << "The program will output the longest path of the binary tree." << endl;
int pathLength = , longestLength = ;
elementType *path1 = new char[ BT1.numberOfBTreeNode( BT1.getNodePoint() ) ];
elementType *longestPath = new char[ BT1.numberOfBTreeNode( BT1.getNodePoint() ) ];
BT1.binaryTreeLongestPath( BT1.getNodePoint(), path1, pathLength, longestPath, longestLength );
cout << "Longest path:" << endl;
for( int i = longestLength; i >= ; i -- )
{
if( i!= )
cout << longestPath[i] << " --> ";
else
cout << longestPath[i] << endl; }
} int main(int argc, char* argv[])
{
//test1();
test2();
//test3();
//test4();
//test5();
//test6();
//test7();
//test8();
//test9();
//test10();
return ;
}
6.6 调试过程中出现的bug总结
往事不堪回首。
刚开始应该写成将data写成string或者直接将整个函数写成模板的，写完了最后测试时才发现现在的写法有诸多不便；但修改的话就又要重构一遍，懒得整了。
刚开始尝试写英文注释的，后面知难而退了；不过原来的英文注释我保留了。
附测试数据及对应二叉树图形：
bt4.btr
BinaryTree
A 0 1
B 0 1
C 0 1
D 0 0
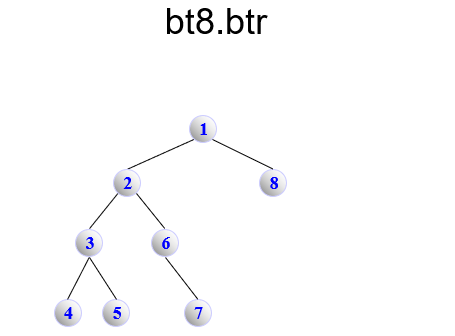
bt8.btr
BinaryTree
1 1 1
2 1 1
3 1 1
4 0 0
5 0 0
6 0 1
7 0 0
8 0 0
bt9.btr
BinaryTree
a 1 1
b 1 1
d 0 0
e 1 1
g 0 0
h 0 0
c 1 0
f 0 1
i 0 0
bt10.btr
BinaryTree
A 1 1
B 1 1
C 0 0
D 1 0
E 0 0
F 1 1
G 0 1
H 0 0
I 1 0
J 0 0
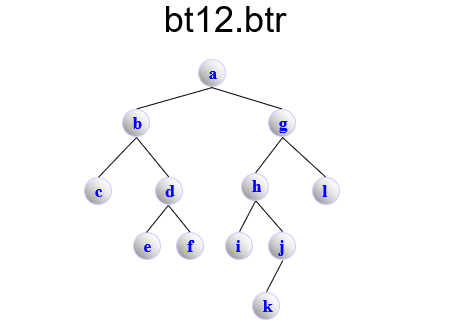
bt12.btr
BinaryTree
A 1 1
B 1 1
C 0 0
D 1 1
E 0 0
F 0 0
G 1 1
H 1 1
I 0 0
J 1 0
K 0 0
L 0 0
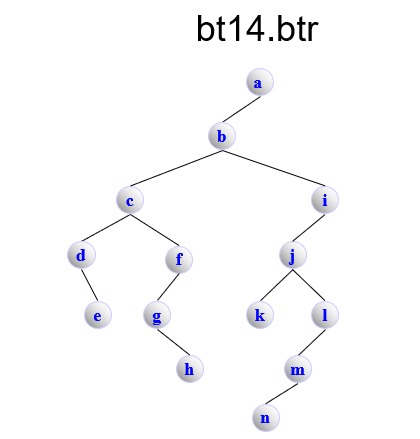
bt14.btr
BinaryTree
A 1 0
B 1 1
C 1 1
D 0 1
E 0 0
F 1 0
G 0 1
H 0 0
I 1 0
J 1 1
K 0 0
L 1 0
M 1 0
N 0 0
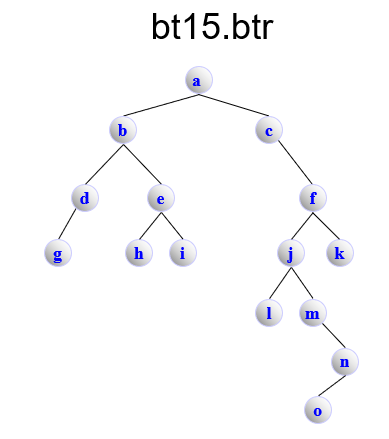
bt15.btr
BinaryTree
A 1 1
B 1 1
D 1 0
G 0 0
E 1 1
H 0 0
I 0 0
C 0 1
F 1 1
J 1 1
L 0 0
M 0 1
N 1 0
O 0 0
K 0 0
bt21.btr
BinaryTree
a 1 1
b 1 1
c 1 1
d 1 1
e 0 0
f 0 0
g 0 0
h 1 1
i 0 0
j 0 0
k 1 1
l 1 1
m 0 0
n 0 0
o 1 1
p 0 1
q 0 0
r 1 1
s 0 0
t 1 0
u 0 0
bt261.btr
BinaryTree
a 1 1
b 1 1
c 1 1
d 1 1
e 0 0
f 0 0
g 1 0
h 0 0
i 1 1
j 0 1
k 0 0
l 1 0
m 0 0
n 1 1
o 1 1
p 1 1
q 0 0
r 0 0
s 0 0
t 1 1
u 1 1
v 0 0
w 0 0
x 1 1
y 0 0
z 0 0
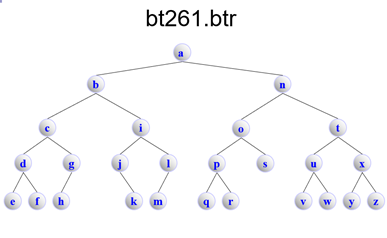
bt262.btr
BinaryTree
a 1 1
b 1 1
c 1 1
d 0 1
e 1 1
f 0 1
g 0 0
h 1 1
i 0 0
j 0 0
k 1 1
l 0 0
m 0 0
n 1 1
o 0 0
p 0 0
q 1 1
r 0 1
s 1 1
t 0 0
u 0 0
v 1 1
w 0 1
x 0 0
y 0 1
z 0 0
full4.btr
BinaryTree
a 1 1
b 1 1
c 1 1
d 0 0
e 0 0
f 1 1
g 0 0
h 0 0
i 1 1
j 1 1
k 0 0
l 0 0
m 1 1
n 0 0
o 0 0
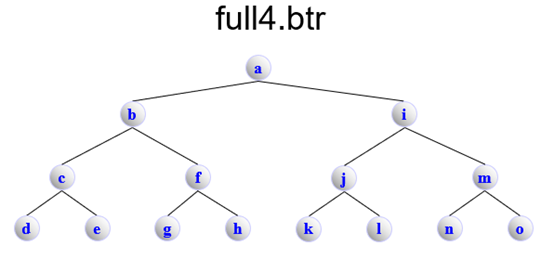
full5.btr
BinaryTree
a 1 1
b 1 1
c 1 1
d 1 1
e 0 0
f 0 0
g 1 1
h 0 0
i 0 0
j 1 1
k 1 1
l 0 0
m 0 0
n 1 1
o 0 0
p 0 0
q 1 1
r 1 1
s 1 1
t 0 0
u 0 0
v 1 1
w 0 0
x 0 0
y 1 1
z 1 1
1 0 0
2 0 0
3 1 1
4 0 0
5 0 0
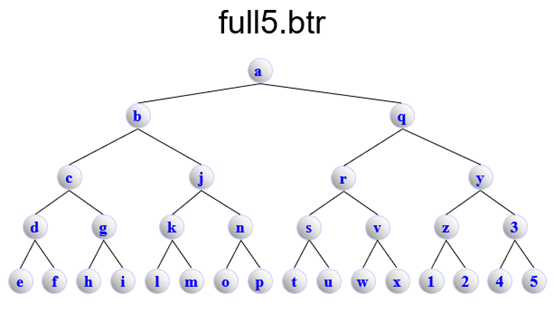
数据结构实验6：C++实现二叉树类的更多相关文章
- SDUT 3346 数据结构实验之二叉树七：叶子问题
数据结构实验之二叉树七:叶子问题 Time Limit: 1000MS Memory Limit: 65536KB Submit Statistic Problem Description 已知一个按 ...
- SDUT 3345 数据结构实验之二叉树六：哈夫曼编码
数据结构实验之二叉树六:哈夫曼编码 Time Limit: 1000MS Memory Limit: 65536KB Submit Statistic Problem Description 字符的编 ...
- SDUT 3340 数据结构实验之二叉树一：树的同构
数据结构实验之二叉树一:树的同构 Time Limit: 1000MS Memory Limit: 65536KB Submit Statistic Problem Description 给定两棵树 ...
- SDUT 3344 数据结构实验之二叉树五：层序遍历
数据结构实验之二叉树五:层序遍历 Time Limit: 1000MS Memory Limit: 65536KB Submit Statistic Problem Description 已知一个按 ...
- SDUT OJ 数据结构实验之二叉树八：（中序后序）求二叉树的深度
数据结构实验之二叉树八:(中序后序)求二叉树的深度 Time Limit: 1000 ms Memory Limit: 65536 KiB Submit Statistic Discuss Probl ...
- SDUT OJ 数据结构实验之二叉树七：叶子问题
数据结构实验之二叉树七:叶子问题 Time Limit: 1000 ms Memory Limit: 65536 KiB Submit Statistic Discuss Problem Descri ...
- SDUT OJ 数据结构实验之二叉树六：哈夫曼编码
数据结构实验之二叉树六:哈夫曼编码 Time Limit: 1000 ms Memory Limit: 65536 KiB Submit Statistic Discuss Problem Descr ...
- SDUT OJ 数据结构实验之二叉树五：层序遍历
数据结构实验之二叉树五:层序遍历 Time Limit: 1000 ms Memory Limit: 65536 KiB Submit Statistic Discuss Problem Descri ...
- SDUT OJ 数据结构实验之二叉树四：（先序中序）还原二叉树
数据结构实验之二叉树四:(先序中序)还原二叉树 Time Limit: 1000 ms Memory Limit: 65536 KiB Submit Statistic Discuss Problem ...
随机推荐
- C. Coconut（2017 ACM-ICPC 亚洲区（乌鲁木齐赛区）网络赛）
额,只是一道签到题,emmm直接代码: #include <cstdio> #include <cstring> #include <algorithm> usin ...
- SpringMVC + ajax
1.ajax 返回汉字乱码 解决方法: http://blog.sina.com.cn/s/blog_5f39177b0101it7h.html //方案一 response.setCharacter ...
- Kruskal HDOJ 1863 畅通工程
题目传送门 /* 此题为:HDOJ 1233 + HDOJ 1232 */ #include <cstdio> #include <algorithm> #include &l ...
- FACVSPOW - Factorial vs Power 数学方法 + 二分
http://www.spoj.com/problems/FACVSPOW/ 求解n! > a^n最小的整数n 对于有n!和a^n的东西,一般是取ln 然后就是求解 (ln(1) + ln(2) ...
- 基于坐标的自动化测试神器---Total Control快速入门
1.Total Control简单介绍 一款能够在PC上控制手机的软件,同时可以使用PC 触摸屏.鼠标.键盘, 全面操控 Android 手机,只需通过 USB 或 WiFi 连接手机至电脑,即可随时 ...
- subprocess模块详解2
1.call() 和run功能类似,都是接受一个列表里的参数. >>> import subprocess >>> a = subprocess.call([&qu ...
- 【HEVC简介】SAO-Sample Adaptive Offset， 样本自适应偏移量
paper: Sample Adaptive Offset for HEVC <HEVC标准介绍.HEVC帧间预测论文笔记>系列博客,目录见:http://www.cnblogs.com/ ...
- redis源码分析之事务Transaction（下）
接着上一篇,这篇文章分析一下redis事务操作中multi,exec,discard三个核心命令. 原文地址:http://www.jianshu.com/p/e22615586595 看本篇文章前需 ...
- 获取父页面的dom元素
$("li.jericho_tabs", window.top.document); 上面的代码意思是获取父页面的li元素,class为jericho_tabs的所有元素.
- （转）使用JDK中的Proxy技术实现AOP功能
http://blog.csdn.net/yerenyuan_pku/article/details/52863780 AOP技术在企业开发中或多或少都会用到,但用的最多的大概就是做权限系统时,在做权 ...