poj 3517(约瑟夫环问题)

And Then There Was One

Time Limit: 5000MS		Memory Limit: 65536K
Total Submissions: 4873		Accepted: 2598

Description

Let’s play a stone removing game.

Initially, n stones are arranged on a circle and numbered 1, …, n clockwise (Figure 1). You are also given two numbers k and m. From this state, remove stones one by one following the rules explained below, until only one remains. In step 1, remove stone m. In step 2, locate the k-th next stone clockwise from m and remove it. In subsequent steps, start from the slot of the stone removed in the last step, make k hops clockwise on the remaining stones and remove the one you reach. In other words, skip (k − 1) remaining stones clockwise and remove the next one. Repeat this until only one stone is left and answer its number. For example, the answer for the case n = 8, k = 5, m = 3 is 1, as shown in Figure 1.

Initial state	Step 1	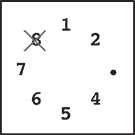Step 2	Step 3	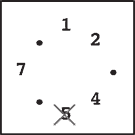Step 4
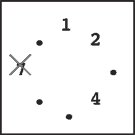Step 5	Step 6	Step 7	Final state

Figure 1: An example game

Initial state: Eight stones are arranged on a circle.

Step 1: Stone 3 is removed since m = 3.

Step 2: You start from the slot that was occupied by stone 3. You skip four stones 4, 5, 6 and 7 (since k = 5), and remove the next one, which is 8.

Step 3:
You skip stones 1, 2, 4 and 5, and thus remove 6. Note that you only
count stones that are still on the circle and ignore those already
removed. Stone 3 is ignored in this case.

Steps 4–7:
You continue until only one stone is left. Notice that in later steps
when only a few stones remain, the same stone may be skipped multiple
times. For example, stones 1 and 4 are skipped twice in step 7.

Final State: Finally, only one stone, 1, is on the circle. This is the final state, so the answer is 1.

Input

The input consists of multiple datasets each of which is formatted as follows.

n k m

The
last dataset is followed by a line containing three zeros. Numbers in a
line are separated by a single space. A dataset satisfies the following
conditions.

2 ≤ n ≤ 10000, 1 ≤ k ≤ 10000, 1 ≤ m ≤ n

The number of datasets is less than 100.

Output

For
each dataset, output a line containing the stone number left in the
final state. No extra characters such as spaces should appear in the
output.

Sample Input

8 5 3
100 9999 98
10000 10000 10000
0 0 0

Sample Output

1
93
2019

Source

Japan 2007

题目描述 ： n个数排成一圈，第一次删除，以后每数k个数删除一次。求最后一次被删除的数。

假设数字标号为0,1,2,3，，，n-1,。第一次删除的数是k，那么还剩0,1,2，3，，，k-1,k+1,k+2,,,,n-1;

那么问题就转化为求这n-1个数，最后一次被删除的数？，最优子结构，定义状态f[n]代表对n个数进行操作，最后一次被删除的数。

我们需要重新对这n-1个数重新编号，k+1,k+2,k+3,,,n-1,0,1,2,3,4, ,,k-1,重新编号为，0，1,2,3,4，5，，，，n-1.

f[n]与f[n-1]有什么关系呢？f[n]=(f[n-1]+k)%n;因为只是重新编号，所以我们只需将n-1个数所求的最后一个数的序号转化为ｎ个数要求的最后一个数的序号.

题目要求第一次删除的是ｍ，那么我们考虑－k+1,开始数ｋ个数，那么第一次删除的就是０号元素，而且如果０号元素是ｍ的话，那么f[n]号元素就为f[n]+m.

int answer=（m-k+1+f[n]）%n;

if(answer<=0)

answer+=n;

不能写成(answer+n)%n,因为answer==0,n%n==0.

#include <iostream>
#include <cstdio>
//#include <strng>
#include <cstring>
using namespace std;
 
int n,m,k;
int f[];
void init()
{
  memset(f,,sizeof(f));
}
 
void solve()
{
 
  for(int i=;i<=n;i++)
   f[i]=(f[i-]+k) % i;
   int answer;
   answer=(m-k++f[n]) % n;
   if(answer<=)
   answer=(answer+n)%n;   //不能这么写，如果answer==0，答案就为0了
   printf("%d\n",answer);
 
}
 
int main()
{
 
  // freopen("test.txt","r",stdin);
    while(~scanf("%d%d%d",&n,&k,&m))
    {
      if(n== && m== && k==)
      break;
      init();
      solve();
    }
 
    return ;
}