[HAOI2011]Problem b 题解
题目大意:
对于给出的n个询问,每次求有多少个数对(x,y),满足a≤x≤b,c≤y≤d,且gcd(x,y)=k。
思路:
设f(k)为当1≤x≤n,1≤y≤m,且n≤m,使gcd(x,y)=k的数对(x,y)的对数,g(k)为当1≤x≤n,1≤y≤m,且n≤m,使k|gcd(x,y)的数对(x,y)的对数。则 ,莫比乌斯反演,得
,莫比乌斯反演,得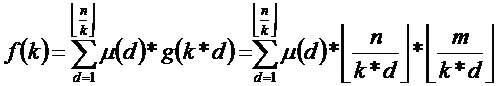 。
。 和
和 会有连续的一段相同且相同的为一定连续的一段,可证最多有2√n和2√m段,分块处理,对于每个询问可O(√n)解决。
会有连续的一段相同且相同的为一定连续的一段,可证最多有2√n和2√m段,分块处理,对于每个询问可O(√n)解决。
代码:
#include<cstdio>
#include<iostream>
using namespace std;
const int M=;
int k,prime[M],mu[M],s[M];
bool flag[M]; int read()
{
int x=; char ch=getchar();
while (ch<'' || ch>'') ch=getchar();
while (ch>='' && ch<='') x=(x<<)+(x<<)+ch-,ch=getchar();
return x;
} void getmu(int n)
{
mu[]=;
int i,j,k,cnt=;
for (i=;i<n;++i)
{
if (!flag[i]) prime[++cnt]=i,mu[i]=-;
for (j=;j<=cnt && (k=i*prime[j])<n;++j)
{
flag[k]=;
if (!(i%prime[j])) { mu[k]=; break; }
mu[k]=-mu[i];
}
}
for (i=;i<n;++i) s[i]=s[i-]+mu[i];
} int sum(int n,int m)
{
if (n>m) swap(n,m);
n=n/k,m=m/k;
int i,j,ans=;
for (i=;i<=n;i=j+)
{
j=min(n/(n/i),m/(m/i));
ans=ans+(s[j]-s[i-])*(n/i)*(m/i);
}
return ans;
} int main()
{
getmu(M);
for (int T=read();T;--T)
{
int a=read(),b=read(),c=read(),d=read();k=read();
printf("%d\n",sum(b,d)-sum(a-,d)-sum(c-,b)+sum(a-,c-));
}
return ;
}
[HAOI2011]Problem b 题解的更多相关文章
- BZOJ2298:[HAOI2011]problem a——题解
https://www.lydsy.com/JudgeOnline/problem.php?id=2298 https://www.luogu.org/problemnew/show/P2519 一次 ...
- BZOJ2301:[HAOI2011]Problem b——题解
http://www.lydsy.com/JudgeOnline/problem.php?id=2301 https://www.luogu.org/problemnew/show/P2522 对于给 ...
- BZOJ2301: [HAOI2011]Problem b[莫比乌斯反演 容斥原理]【学习笔记】
2301: [HAOI2011]Problem b Time Limit: 50 Sec Memory Limit: 256 MBSubmit: 4032 Solved: 1817[Submit] ...
- bzoj 2301: [HAOI2011]Problem b
2301: [HAOI2011]Problem b Time Limit: 50 Sec Memory Limit: 256 MB Submit: 3757 Solved: 1671 [Submit] ...
- HAOI2011 problem b
2301: [HAOI2011]Problem b Time Limit: 50 Sec Memory Limit: 256 MBSubmit: 1047 Solved: 434[Submit][ ...
- BZOJ 2298: [HAOI2011]problem a 动态规划
2298: [HAOI2011]problem a Time Limit: 1 Sec Memory Limit: 256 MB 题目连接 http://www.lydsy.com/JudgeOnli ...
- 【BZOJ2302】[HAOI2011]Problem C(动态规划)
[BZOJ2302][HAOI2011]Problem C(动态规划) 题面 BZOJ 洛谷 题解 首先如果\(m=0\)即没有特殊限制的话,那么就和这道题目基本上是一样的. 然而这题也有属于这题的性 ...
- [POI2007]ZAP-Queries && [HAOI2011]Problem b 莫比乌斯反演
1,[POI2007]ZAP-Queries ---题面---题解: 首先列出式子:$$ans = \sum_{i = 1}^{n}\sum_{j = 1}^{m}[gcd(i, j) == d]$$ ...
- 【BZOJ2298】[HAOI2011]problem a DP
[BZOJ2298][HAOI2011]problem a Description 一次考试共有n个人参加,第i个人说:“有ai个人分数比我高,bi个人分数比我低.”问最少有几个人没有说真话(可能有相 ...
随机推荐
- TSP+Floyd BestCoder Round #52 (div.2) 1002 Victor and Machine
题目传送门 题意:有中文版的 分析:(出题人的解题报告)我们首先需要预处理出任意两个国家之间的最短距离,因为数据范围很小,所以直接用Floyd就行了.之后,我们用f[S][i]表示访问国家的情况为S, ...
- 12c debug 转 12C 连接CDB和PDB
来源:David Dai -- Focus on Oracle 连接到CDB 12c debug 和普通实例一样的连接. 指定ORACLE_SID 以后可以使用OS认证,也可以使用密码进行连接. [o ...
- OAuth 开放授权 Open Authorization
http://oauth.net/ http://tools.ietf.org/html/rfc6749 http://reg.163.com/help/help_oauth2.html 网易通行证O ...
- outlook 通讯录分类--2017年1月16日--对联系人分类管理
outlook功能多,复杂,导致打开界面就晕,通讯录分类 问:在Outlook 中,随着联系人数量的增多,亲朋好友.同事.客户的信息混杂在一起,每次发邮件都要用很长时间才能从联系人列表中找到需要的人. ...
- 移动设备访问使用百度js跳转
以下为代码,可放置在网站foot底部文件,或者haead顶部文件,建议将代码放在网站顶部,这样可以实现手机访问立即跳转! <script src="http://siteapp.bai ...
- Java编程思想总结笔记Chapter 5
初始化和清理是涉及安全的两个问题.本章简单的介绍“垃圾回收器”及初始化知识. 第五章 初始化与清理 目录:5.1 用构造器确保初始化5.2 方法重载5.3 默认构造器5.4 this关键字5.5 清 ...
- R in action读书笔记(19)第十四章 主成分和因子分析
第十四章:主成分和因子分析 本章内容 主成分分析 探索性因子分析 其他潜变量模型 主成分分析(PCA)是一种数据降维技巧,它能将大量相关变量转化为一组很少的不相关变量,这些无关变量称为主成分.探索性因 ...
- Petri网的工具
需要寻找 Petri 网的工具的朋友可以在 http://www.informatik.uni-hamburg.de/TGI/PetriNets/tools/complete_db.html 里面找一 ...
- Objective-C 里面的类对象复用小结
OC 提供了单继承 (Inheritance), Category, Extension, Protocol 这几种基本的类与对象层面的复用机制,作一小结. 在这几个机制中,继承提供了纵向的复用,可以 ...
- 【PostgreSQL-9.6.3】一般视图
PG视图分为两种,一种是物化视图,一种是一般视图.本篇文章主要写一般视图哪些事儿.所谓一般视图,通俗点说,就是由查询语句定义的虚拟表.视图中的数据可能来自一张或多张表. 1. 视图创建语句 CREAT ...
