FPGA-信号边缘检测

　　在FPGA逻辑电路中，输入信号的边缘检测是一个常用的操作，这算是FPGA的基本功之一。

　　信号边缘检测应用十分广泛，例如：通信协议的时序操作，按键的检测等，都应用到按键的检测。按键的检测分为上升沿和下降沿两种，基本的检测思想是一致的。本博客的思想是先介绍阻塞和非阻塞两种赋值，在理解这个的基础上然后去分析边缘检测。这里，首先分析一下Verilog语言中阻塞赋值（=）和非阻塞赋值（<=）的区别，给出相应的案例来帮助理解：

module prj1(in,b,c,d,clk,rst_n);

input in;
input clk;
input rst_n;
output b,c,d;
reg b,c,d;

always @(posedge clk or negedge rst_n) begin
    if(!rst_n) begin
        b <=;
        c <=;
        d <=;
    end
    else begin
        b <=in;
        c <=b;
        d <=c;
        end
    end
endmodule

这个目的是为了展示非阻塞赋值过程中的时序变化，对应的RTL电路图和仿真波形如下图：

从仿真图可以看书，b,c,d是在每个时钟后依次传递的，如果采用阻塞赋值，如果in改变，那么b,c,d立刻改变，这个就在这里不给出仿真。

阻塞赋值和非阻塞赋值的另外一个区别在于综合的时候，如果输出只有d，bc作为中间变量，阻塞赋值在综合的过程中会自动省略掉中间过程。给出如下仿真，理解更为清楚

module prj1(in,b,c,clk,rst_n);

input in;
input clk;
input rst_n;
output b,c;
reg b,c, e,f, m,n;
/* <= */
always @(posedge clk or negedge rst_n) begin
    if(!rst_n) b <=;
    else begin
        e <=in;
        f <=e;
        b <=f;
        end
    end
/* = */
always @(posedge clk or negedge rst_n) begin
    if(!rst_n) c=;
    else begin
        m = in;
        n = m;
        c = n;
        end
    end
endmodule

综合后结果如图，可以看出，采用阻塞赋值，综合后的逻辑单元只有一个，中间变量m,n直接省去了。

信号边缘检测：

回归主题，现在谈谈边缘检测思想。我们姑且这么叫：b<=in; status<=b 称为 in到status的一次延迟赋值（延迟时间为一个时钟），in到status的n次延迟就以此类推。

输入　　　　　　in:     1 1 1 1 1 0 0 0 0 0 0 0 1 1 1

一次延迟　　　delay1: x 1 1 1 1 1 0 0 0 0 0 0 0 1 1 1

输入取反  　　 ~in：    0 0 0 0 0 1 1 1 1 1 1 1 0 0 0

一次延迟取反 ~delay1:x 0 0 0 0 0 1 1 1 1 1 1 1 0 0 0

上升沿检测：(~delay1)&in --in bit13

下降沿检测：(~in)&delay1 --in bit6

说明：针对边缘毛刺多的地方，比如按键的消除抖动，这里面的延迟需要设定够大（比较好的按键消抖时间20ms左右），通过对时钟的分频进行一次延迟赋值，这样子就能够消除延迟中的抖动，并且能够很好的检测出来按键的边缘。

给出一个简单的边缘检测程序：

module prj1(clk,rst_n,in,pos_edge,neg_edge);

input clk,rst_n,in;
output pos_edge,neg_edge;

reg delay1;
reg pos_edge,neg_edge;

always @(posedge clk or negedge rst_n) begin
    if(!rst_n) begin
        delay1<=;
        pos_edge<=;
        neg_edge<=;
        end
    else begin
        delay1<=in;
        pos_edge <=(~delay1)&in;
        neg_edge <=(~in)&delay1;
    end
end

endmodule

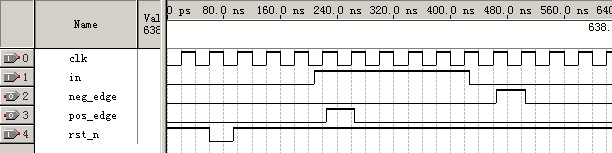
仿真结果如图：