51NOD 1154 回文串的划分(DP)
思路:参考了网上,思路很清奇,借助vis[i][j]来表示从i到j是否为回文串,回文串这边是用的双重循环来写的;dp[i]用来表示以i结尾的字符串最少的回文串有多长。
#include<cstring>
#include<iostream>
#include<algorithm>
using namespace std;
const int maxn = 5e3 + ;
int dp[maxn];//dp[i]表示的是以第i个字符结尾的最少划分数
//dp[i] = min(dp[i],dp[j]+1) 当j到i是回文串时
char s[maxn];
bool vis[maxn][maxn];//vis[i][j]表示i到j的字符串是否是回文串
int main(){ gets(s);
int len = strlen(s);
memset(vis, , sizeof vis); for (int i = ; i < len; i++)
vis[i][i] = ; dp[] = ;
for (int i = ; i < len; i++){
dp[i] = i;
dp[i] = min(dp[i], dp[i - ] + ); for (int j = i - ; j >= ; j--){
if (j == i - && s[i] == s[j]){
if (j - >= )dp[i] = min(dp[i], dp[j - ] + );
else dp[i] = ;
vis[j][i] = ;
}
else if (vis[j + ][i - ] && s[i] == s[j]){
if (j - >= )dp[i] = min(dp[i], dp[j - ] + );
else dp[i] = ;
vis[j][i] = ;
}
}
}
cout << dp[len - ] << endl;
return ;
}
51NOD 1154 回文串的划分(DP)的更多相关文章
- 51nod 1154 回文串划分
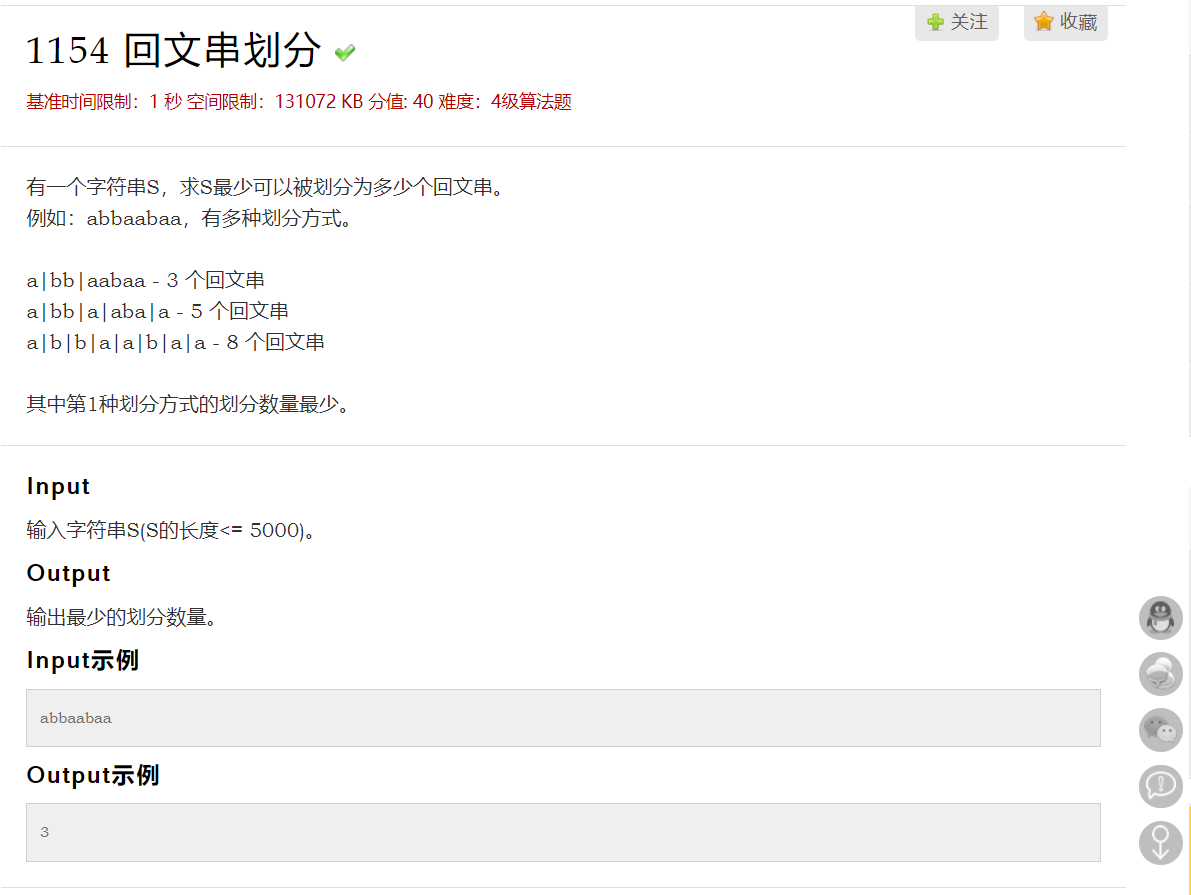
1154 回文串划分 基准时间限制:1 秒 空间限制:131072 KB 分值: 40 难度:4级算法题 收藏 关注 有一个字符串S,求S最少可以被划分为多少个回文串. 例如:abbaabaa,有 ...
- 51Nod - 1154 回文串划分(最少回文串dp)
回文串划分 有一个字符串S,求S最少可以被划分为多少个回文串. 例如:abbaabaa,有多种划分方式. a|bb|aabaa - 3 个回文串 a|bb|a|aba|a - 5 个回文串 a|b ...
- 1154 回文串划分(DP+Manacher)
1154 回文串划分 基准时间限制:1 秒 空间限制:131072 KB 分值: 40 难度:4级算法题 有一个字符串S,求S最少可以被划分为多少个回文串. 例如:abbaabaa,有多种划分方式. ...
- 51nod 1595 回文度 | 马拉车Manacher DP
51nod 1595 回文度 题目描述 如果长度为n的字符串是一个回文串,同时它的长度为floor(n/2)的前缀和后缀是K-1度回文串,则这个字符串被称为K度回文串.根据定义,任何字符串(即使是空字 ...
- UVA - 11584 Partitioning by Palindromes(划分成回文串)(dp)
题意:输入一个由小写字母组成的字符串,你的任务是把它划分成尽量少的回文串,字符串长度不超过1000. 分析: 1.dp[i]为字符0~i划分成的最小回文串的个数. 2.dp[j] = Min(dp[j ...
- 51Nod 1092 回文字符串(LCS + dp)
51Nod 1092 数据结构暑假作业上出现的一题,学习了一下相关算法之后,找到了oj测试能AC. 1.回文串是一种中心对称的结构,这道题可以转变为求最长回文子序列长度的题目.(子序列:可以不连续) ...
- cf1140E 回文串+染色方案dp
有点硬核的dp..要用到一个结论.. /* 把原串拆成奇偶串,再拆成极大连续的-1串:该串两端都是非-1数,中间都是-1,并且下标要么都是偶数,要么都是技术 然后对所有这些串进行dp,dp[i][0] ...
- 便宜的回文串(区间DP)
题目链接:便宜的回文串 这道题刚开始其实还是没有思路的.没办法,只能看题解了... 其实我们在思考问题时,考虑到一段串增或减时会改变它的长度,所以转移时会麻烦... 但其实不用考虑那么多的问题,我们只 ...
- 51nod_1154 回文串的划分
说实话..最开始看这题感觉一定好难...好高大上...我的马拉车还不熟....这种..但是本着做不出来也要至少看看的心态,吧个题看完了..然后简单的想了想,好像是个挺直观的动态规划,因为看到数据几乎就 ...
随机推荐
- MySQL5.7修改字符集
本人安装的mysql版本是5.7.20,安装好mysql后就要对字符集进行修改了,于是照着网上的大部分教程说的去安装目录找一个my-default.ini文件,然后重命名为my.ini,再对其进修改字 ...
- 20. Extjs学习笔记——Ext.data.JsonStore使用说明
Ext.data.JsonStore继承于Ext.data.Store,使得从远程JSON数据创建stores更为方便的简单辅助类.JsonStore合成了Ext.data.HttpProxy与Ext ...
- mysql——免安装配置
1.下载 (1)下载地址:https://dev.mysql.com/downloads/mysql/ (2)选择下载 2.配置环境变量 (1)解压目录:D:\mysql-8.0.16-winx64 ...
- JavaScript--DOM删除节点removeChild()
删除节点removeChild() removeChild() 方法从子节点列表中删除某个节点.如删除成功,此方法可返回被删除的节点,如失败,则返回 NULL. 语法: nodeObject.remo ...
- 转载使用 ContentObsever 拦截短信,获取短信内容
在一些应用上,比如手机银行,QQ,微信等,很多时候我们都需要通过发送验证码到手机上,然后把验证码填上去,然后才能成功地继续去做下面一步事情. 而如果每次我们都要离开当前界面,然后去查收短信,记住验证码 ...
- 三分 HDOJ 3714 Error Curves
题目传送门 /* 三分:凹(凸)函数求极值 */ #include <cstdio> #include <algorithm> #include <cstring> ...
- Linq 内连接和外连接(转载)
一.内连接 Model1Container model = new Model1Container(); //内连接 var query = from s in model.Student join ...
- 292 Nim Game Nim游戏
您和您的朋友,两个人一起玩 Nim游戏:桌子上有一堆石头,每次你们轮流拿掉 1 到 3 块石头. 拿掉最后一块石头的人就是胜利者.由您来开局.你们两个都是聪明人,相信都有最佳的游戏策略. 请编写一个函 ...
- Linux 介绍快速浏览
Linux 介绍 内核 库: .so 共享对象,windows:dll 动态链接库 应用程序 Linux的基本原则:1.由目的单一的小程序组成:组合小程序完成复杂任务:2.一切皆文件:3.尽量避免捕获 ...
- Java学习笔记-eclipse配置
一.配置Java环境变量 JAVA_HOME:D:\Program Files\Java\jdk1.7.0_76 CLASSPATH:.;%JAVA_HOME%\lib\dt.jar;%JAVA_HO ...
