【NOI2012】魔幻棋盘

Description

将要读二年级的小 Q 买了一款新型益智玩具——魔幻棋盘，它是一个N行M列的网格棋盘，每个格子中均有一个正整数。棋盘守护者在棋盘的第X行Y列（行与列均从1开始编号）

并且始终不会移动。棋盘守护者会进行两种操作：

（a）询问：他会以自己所在位置为基础，向四周随机扩展出一块大小不定的矩形区域，向你询问这一区域内所有数的最大公约数是多少。

（b）修改：他会随意挑选棋盘上的一块矩形区域，将这一区域内的所有数同时加上一个给定的整数。

游戏说明书上附有这样一句话“聪明的小朋友，当你连续答对19930324次询问后会得到一个惊喜噢！”。小 Q 十分想得到这个惊喜，于是每天都在玩这个玩具。但由于他粗心大意，经常算错数，难以达到这个目标。于是他来向你寻求帮助，希望你帮他写一个程序来回答棋盘守护者的询问，并保证100%的正确率。

为了简化问题，你的程序只需要完成棋盘守护者的T次操作，并且问题保证任何时刻棋盘上的数字均为不超过$2^{62}-1$的正整数

Input Format

第一行为两个正整数N,M，表示棋盘的大小。 第二行为两个正整数X,Y，表示棋盘守护者的位置。 第三行仅有一个正整数T，表示棋盘守护者将进行次操作。 接下来N行，每行有M个正整数，用来描述初始时棋盘上每个位置的数。 接下来T行，按操作的时间顺序给出T次操作。每行描述一次操作，以一个数字0或1开头： 若以数字0开头，表示此操作为询问，随后会有四个非负整数x1,y1,x2,y2，表示询问的区域是以棋盘守护者的位置为基础向上扩展x1行，向下扩展y1行，向左扩展x2列，向右扩展y2列得到的矩形区域（详见样例）。 若以数字1开头，表示此操作为修改，随后会有四个正整数x1,y1,x2,y2和一个整数c，表示修改区域的上、下边界分别为第x1,x2行，左、右边界分别为第y1,y2列（详见样例），在此矩形区域内的所有数统一加上c（注意c可能为负数）。

Output Format

对于每次询问操作，每行输出一个数，表示该区域内所有数的最大公约数。

Sample Input

2 2
1 1
4
6 12
18 24
0 0 0 1 0
1 1 1 1 2 6
1 2 1 2 2 6
0 0 0 1 1

Sample Output

6
6

Solution

【前置技能】本题是对于一个矩阵求gcd，也就是说是一个二维的问题，那处理一维的问题自然就是前置技能了，对于一个数列，

我们可以发现，$gcd(a_1,a_2,...a_n)=gcd(a_1,a_2-a_1,...,a_n-a_{n - 1})$，有了这个结论我们就可以对于一维的问题用线段树解决了

将其做一个前缀和的差分，以便我们可以得到第一个数，我们将$a_2-a_1,a_3-a_2,...,a_n-a_{n-1}$存入线段树，修改的区间[l,r]时，

实际上就是对于线段树l的位置+k，对于r+1的位置-k（这个可能讲不清楚，可以移步其他博客在回来看）

【错解】有了上面这个结论，我们很容易想到把查询的矩形分成左上角一个点，左边一列，上面一行，右下一块四个部分来解决问题，

开始我也是这么做，然后就把4k+的代码删得只剩线段树了，该做法的问题就在于，如果你修改了一个矩阵那你也需要将这个矩阵拆分成四个部分进行修改

但是你修改左边一列的时候就会发现，这一列中每个位置都对应一行的一个位置，也就是说，如果修改了一列，对应的每行都需修改，这样的复杂度显然是不对的

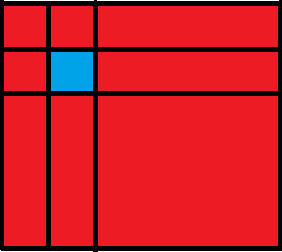
实际上修改时你并无法修改到蓝色这一格，因为修改的时候蓝色这一格是作为一整个方块进行修改的，则询问以其为起始对应行列都会出问题，

【正解】出题人必然也知道上面这个看似正确的错解，那么难道这是一道错题？

显然不是

对于询问，我们发现一个特点，所有询问都是以(x,y)为中心的！

那么我们以(x,y)为坐标原点，建立坐标系切割矩形，我们很容易发现，询问的每个矩形的每个都要么在原点，要么在坐标轴上，要么在四个象限

我们只需要一棵二维线段树记录一下一个矩阵做完差分后的gcd就行了(要不就像我一样傻逼地开了3棵线段树，四个象限用二维线段树，坐标轴用一维线段树)

具体怎么差分呢，在坐标轴上的大家一定都会，我就举一个在第一象限的例子好了

对于第一象限一个点，c[i][j]=a[i][j]-a[i+1][j]-a[i][j+1]+a[i+1][j+1](c表示差分后的值，a表示原矩阵)

为什么这样做？实际上我们要做的事就是减少修改次数，我们发现上面那个差分刚好加两个值，减两个值，而且这四个数刚好相邻构成矩阵，且这个矩阵刚刚刚刚好是向着原点的啊，真的是刚刚刚刚好啊，不选它选谁啊

对于修改操作，我的程序实现还是比较麻烦的，修改也是分为修改坐标轴和修改象限

对于每个象限做的操作大概长这样

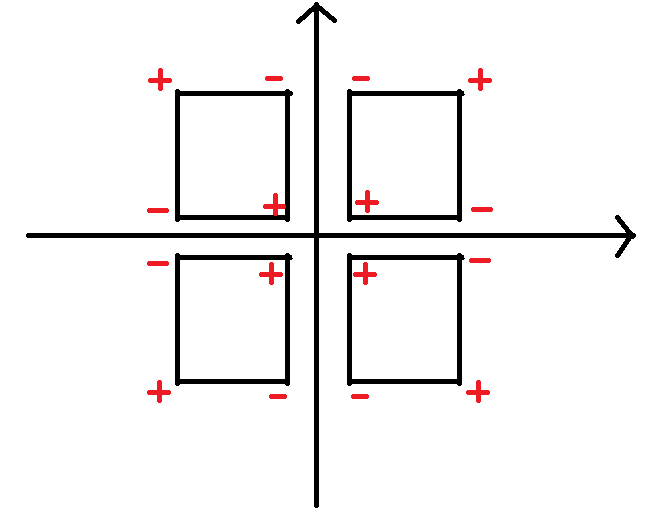
既然差分已经做出来了，那修改也不是难事，就是有一些边界问题需要处理一下，还有一种特殊情况，就是当矩形一条边恰好贴在坐标轴上时，例如贴在x轴上，矩阵向y的正半轴延申，此时矩阵并不包括y的负半轴，但是负半轴的第一个点与原点做差分的时候，差分的结果仍然会-k，当然，边贴在坐标轴上时，象限中的点也会收到一些影响，这个反正乱搞一下就好了

有什么问题看代码吧，私信问我也ok的啊

代码啦~~~(4k+改到7k+,难受）

#include<cstdio>
#include<vector>
#define ll long long
#pragma GCC optimize(2)
const int N=;
ll c[N];
ll abs(ll a){return a>?a:-a;}
ll gcd(ll a,ll b){return (!b)?a:gcd(b,a%b);}
struct r{
    ll g[*N];
    void updata(int id){
        int lson=id<<,rson=id<<|;
        g[id]=gcd(g[lson],g[rson]);
    }
    void build(int l,int r,int id){
        if (l==r){g[id]=c[l];return;}
        int mid=(l+r)>>;
        build(l,mid,id<<);
        build(mid+,r,id<<|);
        updata(id);
        return;
    }
    void modify(int l,int r,int id,int pos,ll val){
        if (l==r){
            g[id]+=val;
            return;
        }
        int mid=(l+r)>>;
        if (pos<=mid)modify(l,mid,id<<,pos,val);
        else modify(mid+,r,id<<|,pos,val);
        updata(id);
    }
    ll query_g(int l,int r,int id,int ql,int qr){
        if (ql<=l&&r<=qr)return g[id];
        int mid=(l+r)>>;
        if (qr<=mid)return query_g(l,mid,id<<,ql,qr);
        else if (ql>mid)return query_g(mid+,r,id<<|,ql,qr);
        else return gcd(query_g(l,mid,id<<,ql,qr),query_g(mid+,r,id<<|,ql,qr));
    }
}row1,cm1,row2,cm2;
struct r1{
    int l,r;ll g;
}t[];
int rt[],tmp,n,m;ll ansp;
void updata(int id){t[id].g=gcd(t[t[id].l].g,t[t[id].r].g);}
void modify(int l,int r,int& id,int x,ll y){
    if (!id)id=++tmp;
    if (l==r){t[id].g+=y;return;}
    int mid=(l+r)>>;
    if (x<=mid)modify(l,mid,t[id].l,x,y);
    else modify(mid+,r,t[id].r,x,y);
    updata(id);
}
void get_new(int l,int r,int& id,int ls,int rs,int x){
    if (!id)id=++tmp;
    t[id].g=gcd(t[ls].g,t[rs].g);
    if (l==r)return;
    int mid=(l+r)>>;
    if (x<=mid)get_new(l,mid,t[id].l,t[ls].l,t[rs].l,x);
    else get_new(mid+,r,t[id].r,t[ls].r,t[rs].r,x);
}
void add(int l,int r,int id,int x,int y,ll z){
    if (l==r){modify(,m,rt[id],y,z);return;}
    int mid=(l+r)>>;
    if (x<=mid)add(l,mid,id<<,x,y,z);
    else add(mid+,r,id<<|,x,y,z);
    get_new(,m,rt[id],rt[id<<],rt[id<<|],y);
}
ll get_gcd(int l,int r,int id,int ql,int qr){
    if (ql<=l&&r<=qr)return t[id].g;
    int mid=(l+r)>>;
    if (ql>mid)return get_gcd(mid+,r,t[id].r,ql,qr);
    else if (qr<=mid)return get_gcd(l,mid,t[id].l,ql,qr);
    else return gcd(get_gcd(l,mid,t[id].l,ql,qr),get_gcd(mid+,r,t[id].r,ql,qr));
}
ll query(int l,int r,int id,int x1,int y1,int x2,int y2){
    if (x1<=l&&r<=x2)return get_gcd(,m,rt[id],y1,y2);
    int mid=(l+r)>>;
    if (x1>mid)return query(mid+,r,id<<|,x1,y1,x2,y2);
    else if (x2<=mid)return query(l,mid,id<<,x1,y1,x2,y2);
    else return gcd(query(l,mid,id<<,x1,y1,x2,y2),query(mid+,r,id<<|,x1,y1,x2,y2));
}
std::vector<ll> v[N];
ll read(){
    int c=getchar(),f=;ll ret=;
    while (c<''||c>''){if (c=='-')f=-;c=getchar();}
    while (c>=''&&c<='')ret=(ret<<)+(ret<<)+c-'',c=getchar();
    return ret*f;
}
int main(){
    n=read(),m=read();
    int x=read(),y=read(),op,x1,y1,x2,y2;
    int T=read();
    for (int i=;i<=n;i++)v[i].push_back();
    for (int j=;j<=m;j++)v[].push_back();
    for (int i=;i<=n;i++)
        for (int j=;j<=m;j++)
            v[i].push_back(read());
    ansp=v[x][y];
    for (int i=x-;i>=;i--)c[i]=v[i][y]-v[i+][y];
    for (int i=x+;i<=n;i++)c[i]=v[i][y]-v[i-][y];
    if (x>)row1.build(,x-,);
    if (x<n)row2.build(x+,n,);
    for (int i=y-;i>=;i--)c[i]=v[x][i]-v[x][i+];
    for (int i=y+;i<=m;i++)c[i]=v[x][i]-v[x][i-];
    if (y>)cm1.build(,y-,);
    if (y<m)cm2.build(y+,m,);
    ll z;
    for (int i=;i<x;i++)
        for (int j=;j<y;j++)z=v[i][j]-v[i+][j]-v[i][j+]+v[i+][j+],add(,n,,i,j,z);
    for (int i=x+;i<=n;i++)
        for (int j=;j<y;j++)z=v[i][j]-v[i-][j]-v[i][j+]+v[i-][j+],add(,n,,i,j,z);
    for (int i=;i<x;i++)
        for (int j=y+;j<=m;j++)z=v[i][j]-v[i+][j]-v[i][j-]+v[i+][j-],add(,n,,i,j,z);
    for (int i=x+;i<=n;i++)
        for (int j=y+;j<=m;j++)z=v[i][j]-v[i-][j]-v[i][j-]+v[i-][j-],add(,n,,i,j,z);
    while (T--){
        op=read();
        x1=read(),y1=read(),x2=read(),y2=read();
        if (!op){
            ll ans=ansp;
            if (x1>&&y1>)ans=gcd(ans,query(,n,,x-x1,y-y1,x-,y-));
            if (x1>&&y2>)ans=gcd(ans,query(,n,,x-x1,y+,x-,y+y2));
            if (x2>&&y1>)ans=gcd(ans,query(,n,,x+,y-y1,x+x2,y-));
            if (x2>&&y2>)ans=gcd(ans,query(,n,,x+,y+,x+x2,y+y2));
            if (x1>)ans=gcd(ans,row1.query_g(,x-,,x-x1,x-));
            if (x2>)ans=gcd(ans,row2.query_g(x+,n,,x+,x+x2));
            if (y1>)ans=gcd(ans,cm1.query_g(,y-,,y-y1,y-));
            if (y2>)ans=gcd(ans,cm2.query_g(y+,m,,y+,y+y2));
            printf("%lld\n",abs(ans));
        }
        else {
            ll k=read();
            if (x>=x1&&x<=x2&&y>=y1&&y<=y2)ansp+=k;
            if(x>=x1&&x<=x2){
                if (y1<y&&y2<y){if (y1>)cm1.modify(,y-,,y1-,-k);cm1.modify(,y-,,y2,k);}
                else if (y1>y&&y2>y){if (y2<m)cm2.modify(y+,m,,y2+,-k);cm2.modify(y+,m,,y1,k);}
                else {
                    if (y1<y&&y1>)cm1.modify(,y-,,y1-,-k);
                    if (y2>y&&y2<m)cm2.modify(y+,m,,y2+,-k);
                }
            }
            if (y>=y1&&y<=y2){
                if (x1<x&&x2<x){if (x1>)row1.modify(,x-,,x1-,-k);row1.modify(,x-,,x2,k);}
                else if (x1>x&&x2>x){if (x2<n)row2.modify(x+,n,,x2+,-k);row2.modify(x+,n,,x1,k);}
                else {
                    if (x1<x&&x1>)row1.modify(,x-,,x1-,-k);
                    if (x2>x&&x2<n)row2.modify(x+,n,,x2+,-k);
                }
            }
            if (x1<x&&y1<y){if (x1>&&y1>)add(,n,,x1-,y1-,k);}
            else if (x1<x&&y1>y){if (x1>)add(,n,,x1-,y1,-k);}
            else if (x1>x&&y1<y){if (y1>)add(,n,,x1,y1-,-k);}
            else if (x1>x&&y1>y)add(,n,,x1,y1,k);
            if (x1<x&&y2<y){if (x1>)add(,n,,x1-,y2,-k);}
            else if (x1<x&&y2>y){if (x1>&&y2<m)add(,n,,x1-,y2+,k);}
            else if (x1>x&&y2<y)add(,n,,x1,y2,k);
            else if (x1>x&&y2>y)if (y2<m)add(,n,,x1,y2+,-k);
            if (x2<x&&y1<y){if (y1>)add(,n,,x2,y1-,-k);}
            else if (x2>x&&y1<y){if (x2<n&&y1>)add(,n,,x2+,y1-,k);}
            else if (x2<x&&y1>y)add(,n,,x2,y1,k);
            else if (x2>x&&y1>y)if (x2<n)add(,n,,x2+,y1,-k);
            if (x2<x&&y2<y)add(,n,,x2,y2,k);
            else if (x2>x&&y2<y){if (x2<n)add(,n,,x2+,y2,-k);}
            else if (x2<x&&y2>y){if (y2<m)add(,n,,x2,y2+,-k);}
            else if (x2>x&&y2>y)if (x2<n&&y2<m)add(,n,,x2+,y2+,k);
            if (x1==x&&x1>){
                if (y1<y&&y1>)add(,n,,x1-,y1-,k);
                else if (y1>y)add(,n,,x1-,y1,-k);
                if (y1==y&&y>)add(,n,,x1-,y1-,k);
                if (y1<=y&&y<=y2)row1.modify(,x-,,x1-,-k);
                if (y2<y)add(,n,,x1-,y2,-k);
                else if (y2>y&&y2<m)add(,n,,x1-,y2+,k);
                if (y2==y&&y<m)add(,n,,x1-,y2+,k);
            }
            if (x2==x&&x2<n){
                if (y1<y&&y1>)add(,n,,x2+,y1-,k);
                else if (y1>y)add(,n,,x2+,y1,-k);
                if (y1==y&&y>)add(,n,,x2+,y1-,k);
                if (y1<=y&&y<=y2)row2.modify(x+,n,,x2+,-k);
                if (y2<y)add(,n,,x2+,y2,-k);
                else if (y2>y&&y2<m)add(,n,,x2+,y2+,k);
                if (y2==y&&y<m)add(,n,,x2+,y2+,k);
            }
            if (y1==y&&y1>){
                if (x1<x&&x1>)add(,n,,x1-,y1-,k);
                else if (x1>x)add(,n,,x1,y1-,-k);
                if (x1<=x&&x<=x2)cm1.modify(,y-,,y1-,-k);
                if (x2>x&&x2<n)add(,n,,x2+,y1-,k);
                else if (x2<x)add(,n,,x2,y1-,-k);
            }
            if (y2==y&&y2<m){
                if (x1<x&&x1>)add(,n,,x1-,y2+,k);
                else if (x1>x)add(,n,,x1,y2+,-k);
                if (x1<=x&&x<=x2)cm2.modify(y+,m,,y2+,-k);
                if (x2>x&&x2<n)add(,n,,x2+,y2+,k);
                else if (x2<x)add(,n,,x2,y2+,-k);
            }
        }
    }
}