Hdu Binary Tree Traversals

Problem Description

        A binary tree is a finite set of vertices that is either empty or consists of a root r and two disjoint binary trees called the left and right subtrees. There are three most important ways in which the vertices of a binary tree can be systematically traversed or ordered. They are preorder, inorder and postorder. Let T be a binary tree with root r and subtrees T1,T2.

In a preorder traversal of the vertices of T, we visit the root r followed by visiting the vertices of T1 in preorder, then the vertices of T2 in preorder.

In an inorder traversal of the vertices of T, we visit the vertices of T1 in inorder, then the root r, followed by the vertices of T2 in inorder.

In a postorder traversal of the vertices of T, we visit the vertices of T1 in postorder, then the vertices of T2 in postorder and finally we visit r.

Now you are given the preorder sequence and inorder sequence of a certain binary tree. Try to find out its postorder sequence.

 

Input

The input contains several test cases. The first line of each test case contains a single integer n (1<=n<=1000), the number of vertices of the binary tree. Followed by two lines, respectively indicating the preorder sequence and inorder sequence. You can assume they are always correspond to a exclusive binary tree.

 

Output

For each test case print a single line specifying the corresponding postorder sequence.

 

Sample Input

9
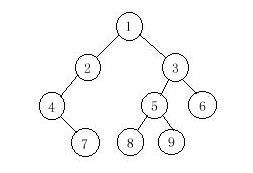
1 2 4 7 3 5 8 9 6
4 7 2 1 8 5 9 3 6

 

Sample Output

7 4 2 8 9 5 6 3 1

 

 

 

 

注: 已知二叉树的前序和中序遍历, 可以唯一确定二叉树的后序遍历, 但如果知道前序和后序,求中序遍历是不可能实现的.

 

算法:

由前序遍历的第一个元素可确定左、右子树的根节点，参照中序遍历又可进一步确定子树的左、

右子树元素。如此递归地参照两个遍历序列，最终构造出二叉树。

由前序和中序结果求后序遍历结果

树的遍历：给你一棵树的先序遍历结果和中序遍历的结果，让你求以后序遍历输出用递归。

每次把两个数组分成三个部分，父节点，左子树，右子树，把父节点放到数组里边，重复此步骤直到重建一棵新树

,  这时，数组里元素刚好是后序遍历的顺序

关键点：

中序遍历的特点是先遍历左子树，接着根节点，然后遍历右子树。这样根节点就把左右子树隔开了。而前序遍历的特点是先访问根节点，从而实现前序遍历结果提供根节点信息，中序遍历提供左右子树信息，从而实现二叉树的重建

【注明】

先序的排列里第一个元素是根，再比较中序的排列里根所在的位置，则能确定左子树，右子树元素个数numleft，numright且在先序排列里，先是一个根，再是numleft个左子树的元素排列，最后是numright个右子树的元素排列。

该过程就是从inorder数组中找到一个根，然后从preorder数组的位置来确定改点到底是左儿子还是右儿子。如此一直循环下去知道一棵完整的数建立完成。

#include <stdio.h>
#include <stdlib.h>

const int MAX = 1000 + 10;
int n,in[MAX],pre[MAX];
typedef struct BITree
{
    int data,index;
    BITree *Left,*Right;
}BiTree,*Tree;

void DFS(Tree &root,int index)
{
    if(root == NULL){
        root = (Tree)malloc(sizeof(BiTree));
        root->data = in[index];
        root->index = index;
        root->Left = NULL;
        root->Right = NULL;
    }else
    {
        if(index < root->index)
          DFS(root->Left,index);
        else
          DFS(root->Right,index);
    }
}

void CreateTree(Tree &root)
{
    int i,j,index;
    root = (Tree)malloc(sizeof(BiTree));
    for(i = 1;i <= n;i++)
      if(in[i] == pre[1])
      {
          root->data = pre[1];
          root->index = i;
          root->Left = NULL;
          root->Right = NULL;
          break;
      }
    index = i;
    for(i = 2;i <= n;i++)
      for(j = 1;j <= n;j++)
         if(in[j] == pre[i])
         {
             if(j < index)
               DFS(root->Left,j);
             else
               DFS(root->Right,j);
             break;
         }
}

void PostOrder(Tree root,int x)
{
    if(root == NULL) return ;
    PostOrder(root->Left,x+1);
    PostOrder(root->Right,x+1);
    if(x == 0)
      printf("%d",root->data);
    else
      printf("%d ",root->data);
}

int main()
{
    int i;
    while(scanf("%d",&n)!=EOF)
    {
        Tree root;
        for(i = 1;i <= n;i++)
          scanf("%d",&pre[i]);
        for(i = 1;i <= n;i++)
          scanf("%d",&in[i]);
        CreateTree(root);
        PostOrder(root,0);
        printf("\n");
    }
    return 0;
}

 

#include <iostream>
#include <cstdio>
using namespace std;

const int MAX = 1000 + 10;
typedef struct BITree
{
    int data;
    BITree *Left,*Right;
    BITree()
    {
        Left = NULL;
        Right = NULL;
    }
}*BiTree;
int pre[MAX],in[MAX];

void BuildTree(BiTree &root,int len,int pst,int ped,int inst,int ined)
{
    int i,left_len = 0;
    if(len<=0)return;          //递归终止的条件
    root = new BITree;
    root->data = pre[pst];
    for(i = inst;i <= ined;i++)
      if(in[i] == pre[pst])
      {
          left_len = i - inst;
          break;
      }
    BuildTree(root->Left,left_len,pst+1,pst+left_len,inst,i-1);
    BuildTree(root->Right,len-left_len-1,pst+left_len+1,ped,i+1,ined);
}

void PostTravel(BITree *root)
{
    if(root)
    {
        PostTravel(root->Left);
        PostTravel(root->Right);
        printf("%d ",root->data);
    }
}

int main()
{
    int i,n;
    BiTree root;
    while(scanf("%d",&n)!=EOF)
    {
        for(i = 1;i <= n;i++)
          scanf("%d",&pre[i]);
        for(i = 1;i <= n;i++)
          scanf("%d",&in[i]);
        BuildTree(root,n,1,n,1,n);
        PostTravel(root->Left);
        PostTravel(root->Right);
        printf("%d\n",root->data);
    }
    return 0;
}