[***]HZOJ 跳房子

一道非常神仙的题.

算法一：对于20%的数据: 模拟，直接走K步,时间复杂度O(K)

算法二：对于40%的数据：走M*N步内必有一个循环节。直接走，找循环节,时间复杂度O(M*N)

正解大概有两种做法（我是第三种……）

1.利用分块思想，一行为一块。用一个数组记录第一列第i行走M步到达的位置jump[i]。在模拟过程中只要一行一行的走，不足一行再一步一步走，按行找循环节,时间复杂度O(M+N)。

更改操作：对于每个更改的单元格（x,y），我们回溯到第一列,找到第一列要更新的区间,更新jump[i] 。因为第一列到(x,y)的行是一个连续区间，在找的过程中，只需记录区间上下边界。复杂度为O（M+N）。

这个的查询比较容易，只是修改比较难搞，我研究了半天，证明了正确性和复杂度，又YY了一下代码实现，觉得细节太多代码又长想了想放弃了，目前xuefeng还在对拍中……这里只说一下修改：

结论1：如果第一列的点（i，1）,(j,1)能到点（x，y），那么（i，1）,(j,1)之间的点都会到（x，y），证明：路线不会交叉，自己YY一下就好啦。

于是设修改map[a][b]为e,那么对a，b左边的三个点分别向后搜索找到最后到的点，然后向前搜索找现在能到这这个点的一段，将这一段的jump都改为向后搜索找到的点。显然这三个点往前回溯找到的区间没有交叉两两之间没有间隙（因为路径不会交叉，手模一下就好啦），而之前能到（a，b）的点一定能到前面的三个点，所以修改（a，b）所影响的点都会考虑到，这样我们就证明了其正确性。然而在回溯时还有一个细节：如果对于每个点都向前分为三个点，那么时间复杂度无法保障，所以只能搜上下边界保证搜索的轨迹是两条线，但是这样对吗？大体是对的，不过有一个细节要考虑：

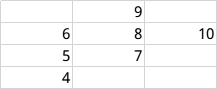
如图，设我们当前在处理10这个点，那么我们应该递归处理9和7而不会去处理8，但是这是7却不是最优的，显然走8才能找到下边界，所以要特判一种情况，当某个点无路可走时，跳的他上（下）面的点（有点难以理解，仔细想一下）。还有一个问题，这样搜索的点又会多不少，时间复杂度能保障吗？实际上是可以的，xuefeng开始觉得这样最坏是n×m的，但是仔细想想会发现，搜索的线路是一条折线，而这条折线的角度只能是45，于是复杂度最坏n+m。

还有一个细节要判断（我估计此时应该没人想打这个算法了……），就是三个点往前搜最后都无路可走的情况。

等旁边的xuefeng调完再放代码吧，不过和我讲的应该会有点（不少）出入……

（此处放代码）

 #include<bits/stdc++.h>
 #define N 2005
 #define LL long long
 #define Inf 0x3f3f3f3f
 using namespace std;
 int n,m,q,len,where_x,to_time;
 int a[N][N],jump[N],vis[N];
 char s[];
 int read(){
     int x=,f=;char ch=getchar();
     while(!isdigit(ch))f=(ch=='-')?-:,ch=getchar();
     while(isdigit(ch))x=x*+ch-'',ch=getchar();
     return x*f;
 }
 inline int _x(int x){
     return (x+n*-)%n+;
 }
 inline int _y(int y){
     return (y+m*-)%m+;
 }
 void get(int &x,int &y){//真
     y=_y(y+);x=_x(x);
     int imax=x,xu=_x(x-),xd=_x(x+);
     if(a[imax][y]<a[xu][y])imax=xu;
     if(a[imax][y]<a[xd][y])imax=xd;
     x=imax;
 }
 void _get(int &x,int y){//假
     y=_y(y+);
     int imax=x,xu=_x(x-),xd=_x(x+);
     if(a[_x(imax)][y]<a[xu][y])imax=x-;
     if(a[_x(imax)][y]<a[xd][y])imax=x+;
     x=imax;
 }

 void work(int l,int r){
     for(int i=l;i<=r;++i){
         int pos=i;int j=;
         do get(pos,j);
         while(j!=);
         jump[i]=pos;
     }
 }
 int L[N],R[N];
 void work_for(pair<int,int>x){
     L[x.second]=R[x.second]=x.first;
     for(int i=x.second;i>=;--i){
         if(L[i]>R[i])return;L[i-]=Inf;R[i-]=-Inf;
         int e1=L[i]-,e2=L[i],e3=L[i]+;
         _get(e1,i-),_get(e2,i-),_get(e3,i-);
         if(e1>=L[i]&&e1<=R[i])L[i-]=L[i]-;
         else if(e2>=L[i]&&e2<=R[i])L[i-]=L[i];
         else if(e3>=L[i]&&e3<=R[i])L[i-]=L[i]+;

         e1=R[i]-,e2=R[i],e3=R[i]+;
         _get(e1,i-),_get(e2,i-),_get(e3,i-);
         if(e3>=L[i]&&e3<=R[i])R[i-]=R[i]+;
         else if(e2>=L[i]&&e2<=R[i])R[i-]=R[i];
         else if(e1>=L[i]&&e1<=R[i])R[i-]=R[i]-;
     }
     pair<int,int>x1=x;
     do get(x1.first,x1.second);
     while(x1.second!=);
     for(int i=L[];i<=R[];++i)jump[_x(i)]=x1.first;
 }
 void Work(int x,int y){
     pair<int,int>e1,e2,e3;
     e1.first=_x(x-),e1.second=_y(y-);
     e2.first=x,e2.second=_y(y-);
     e3.first=_x(x+),e3.second=_y(y-);
     work_for(e1);work_for(e2);work_for(e3);
 }
 void get_tarjan(int row){
     memset(vis,-,sizeof vis);
     for(int i=;i<=n+;++i){//花多少k到达
         if(vis[row]!=-){
             len=i-vis[row];//环长
             where_x=row;//环开始的地方
             to_time=vis[row];//开始时间
             return;
         }
         vis[row]=i;
         row=jump[row];
     }
 }
 int main(){
     //freopen("text.in","r",stdin);
     //freopen("a.out","w",stdout);
     scanf("%d%d",&n,&m);
     for(int i=;i<=n;++i)for(int j=;j<=m;++j)scanf("%d",&a[i][j]);
     work(,n);
     scanf("%d",&q);
     int k,aa,b,e;
     int row=,col=;
     for(int i=;i<=q;++i){
         scanf("%s",s);
         if(s[]=='m'){
             scanf("%d",&k);
             while(col!=&&k){k--;get(row,col);}
             if(k>m){
                 get_tarjan(row);
                 if(k>to_time*m){
                     k-=to_time*m;
                     row=where_x;
                     k%=len*m;
                 }
             }
             while(col!=&&k){k--;get(row,col);}
             while(k>=m){k-=m;row=jump[row];}
             while(k){k--;get(row,col);}
             printf("%d %d\n",row,col);
         }
         else{
             scanf("%d%d%d",&aa,&b,&e);aa=_x(aa);b=_y(b);a[aa][b]=e;
             Work(aa,b);
         }
     }
 }
 /*
 3 6
 204 889 21 921 229 601
 465 187 937 481 241 147
 882 201 8,581 301 457 829
 20
 change
 3 3 581
 change
 1 1 951
 move
 46003169
 move
 93518379
 move
 44247980
 move
 20045342
 change
 1 1 661
 move
 37489600
 move
 95847680
 move
 74183070
 move
 290360
 change
 2 1 233
 move
 24935765
 change
 1 5 924
 move
 91540280
 change
 3 1 790
 change
 3 3 845
 move
 50868396
 move
 69816331
 move
 18735250
 */
 /*
 3 6
 951 889 21 921 229 601
 465 187 937 481 241 147
 882 201 581 301 457 829
 20
 move
 20045342
 */
 /*
 3 6
 2 3
 3 5
 3 1
 3 5
 3 1
 3 1
 2 3
 1 2
 1 4
 1 4
 1 5
 2 3
 */

码风奇丑无比（赠一组数据）

2.可以发现每走一步相当于一次置换，所以可以用线段树维护置换，置换满足结合律，查询可以使用快速幂，而修改只需要修改线段树的一条链。这个我也没打，具体看ex_face的blog

3.我自己YY的跑的超慢但是A掉的算法（其实是因为懒第一种不想打，笨第二种看不懂）。

题解中运用了循环节的思想，目的是将k模掉来降低复杂度，但是这样复杂度取决与循环节长度比较不稳定，那怎么办呢？可以沿用题解中jump数组的做法，而使用倍增，求出第一列每个点走$2^j*m$步到达的点，这样查询就是logk的，那修改呢？重新求倍增数组那个$n*log_m$是跑不了了，但是这样的复杂度是可以接受的，但是jump数组怎么搞呢？暴力m*n求的话肯定会死，所以沿用第二种做法中线段树的思想，每个节点维护一个jump数组，叶子节点jump[j]表示这列第j行走1步到达的行数，那么叶子节点的父亲就表示左边l列走2步到达的行数，上面的节点也一样，那么对于每次修改，我们对其对应的叶子节点Om暴力修改，然后递归处理一条链，总复杂度$n*log_m$，之后重新求倍增数组，总复杂度可以接受。

 #include<iostream>
 #include<cstdio>
 #define LL long long
 #define MAXN 2010
 #define int LL
 #define lo 30
 #define re register
 using namespace std;
 int n,m,Q;
 struct jum
 {
     int jump[MAXN];
     void init()
     {for(int i=;i<=n;i++)jump[i]=i;}
 }tmp;
 void move(re int &x,re int &y);
 void mul(jum &a,jum &b,jum &c)
 {for(int i=;i<=n;i++)c.jump[i]=b.jump[a.jump[i]];}
 struct tree
 {
     jum j;
     int l,r;
     #define l(x) tr[x].l
     #define r(x) tr[x].r
     #define ls(x) (x<<1)
     #define rs(x) (ls(x)+1)
     #define j(x) tr[x].j
 }tr[MAXN*];
 void build(int x,int l,int r)
 {
     l(x)=l,r(x)=r;
     if(l==r)
     {
         int tem=l;
         for(int i=;i<=n;i++)move(j(x).jump[i]=i,tem=l);
         return;
     }
     int mid=(l+r)>>;
     build(ls(x),l,mid);
     build(rs(x),mid+,r);
     mul(j(ls(x)),j(rs(x)),j(x));
 }
 void add(int x,int t)
 {
     if(l(x)==r(x))
     {
         int tem=t;
         for(int i=;i<=n;i++)move(j(x).jump[i]=i,tem=t);
         return;
     }
     int mid=(l(x)+r(x))>>;
     if(t<=mid)add(ls(x),t);
     else       add(rs(x),t);
     mul(j(ls(x)),j(rs(x)),j(x));
 }
 int nowi=,nowj=;
 int map[MAXN][MAXN];
 char op[];int x,a,b,e;
 int ju[MAXN][lo+];
 inline int read();
 signed main()
 {
 //    freopen("jump4.in","r",stdin);

     n=read(),m=read();
     for(int i=;i<=n;i++)
         for(int j=;j<=m;j++)
             map[i][j]=read();

     Q=read();
     build(,,m);
     for(int i=;i<=n;i++)
         ju[i][]=j().jump[i];
     for(re int i=;i<=lo;i++)
         for(int j=;j<=n;j++)
             ju[j][i]=ju[ju[j][i-]][i-];
     for(int i=;i<=Q;i++)
     {
         scanf("%s",op);
         if(op[]=='m')
         {
             x=read();
             while(nowj!=&&x){move(nowi,nowj),x--;}
             for(int k=lo;k>=;k--)
                 if(1ll*(<<k)*m<=x)
                 {nowi=ju[nowi][k],x-=1ll*(<<k)*m;}
             while(x){move(nowi,nowj),x--;}
             printf("%lld %lld\n",nowi,nowj);
         }
         else
         {
             a=read(),b=read(),e=read();
             map[a][b]=e;
             if(b==)add(,m);
             else     add(,b-);
             for(int j=;j<=n;j++)
                 ju[j][]=j().jump[j];
             for(re int j=;j<=lo;j++)
                 for(int k=;k<=n;k++)
                     ju[k][j]=ju[ju[k][j-]][j-];
         }
     }
 }
 inline int read()
 {
     int s=;char a=getchar();
     while(a<''||a>'')a=getchar();
     while(a>=''&&a<=''){s=s*+a-'',a=getchar();}
     return s;
 }
 void move(re int &x,re int &y)
 {
     int t1,t2,t3;
     if(y!=m)
     {
         t1=(x==?map[n][y+]:map[x-][y+]),
         t2=map[x][y+],
         t3=(x==n?map[][y+]:map[x+][y+]);
     }
     else
     {
         t1=(x==?map[n][]:map[x-][]),
         t2=map[x][],
         t3=(x==n?map[][]:map[x+][]);
     }
     if(t1>t2&&t1>t3) x--,y++;
     else if(t2>t1&&t2>t3)y++;
     else             x++,y++;
     if(x==)x=n;
     if(x==n+)x=;
     if(y==)y=m;
     if(y==m+)y=;
 }

最后，附赠xuefeng的玄学乱搞骗到85分（不知道为啥我只能搞到80）的思路（以下纯属乱搞）：

首先是20分的暴力一步一步地模拟（这个应该都会打吧），然后在输入k后加一句话：if(k>10*m)k%=10*m,k+=2*m;看似很选学，实际上是有点依据的，首先循环节肯定是m的整数倍，那为什么选10呢？借用wq学长的话：小了会WA大了会T。那加2*m又是为啥呢？因为在碰到循环节之前会走一个常数。

 #include<bits/stdc++.h>
 #define N 2005
 #define LL long long
 using namespace std;
 int n,m,q;
 int a[N][N];
 char s[];
 inline int read(){
     LL x=,f=;char ch=getchar();
     while(!isdigit(ch))f=ch=='-'?-:,ch=getchar();
     while(isdigit(ch))x=x*+ch-'',ch=getchar();
     return x*f;
 }
 void get(int &x,int &y){
     y=y+==m+?:y+;int xu=x-==?n:x-,xd=x+==n+?:x+;
     if(a[x][y]<a[xu][y])x=xu;if(a[x][y]<a[xd][y])x=xd;
 }
 int main(){
     n=read(),m=read();
     for(int i=;i<=n;++i)for(int j=;j<=m;++j)a[i][j]=read();
     q=read();int k,A,b,e;
     int row=,col=;
     for(int i=;i<=q;++i){
         scanf("%s",s);
         if(s[]=='m'){
             k=read();
             if(k>m*)k%=m*,k+=m*;
             while(k--)get(row,col);
             printf("%d %d\n",row,col);
         }
         else{
             A=read(),b=read(),e=read();
             a[A][b]=e;
         }
     }
 }

代码也放一下吧