51nod 范德蒙矩阵

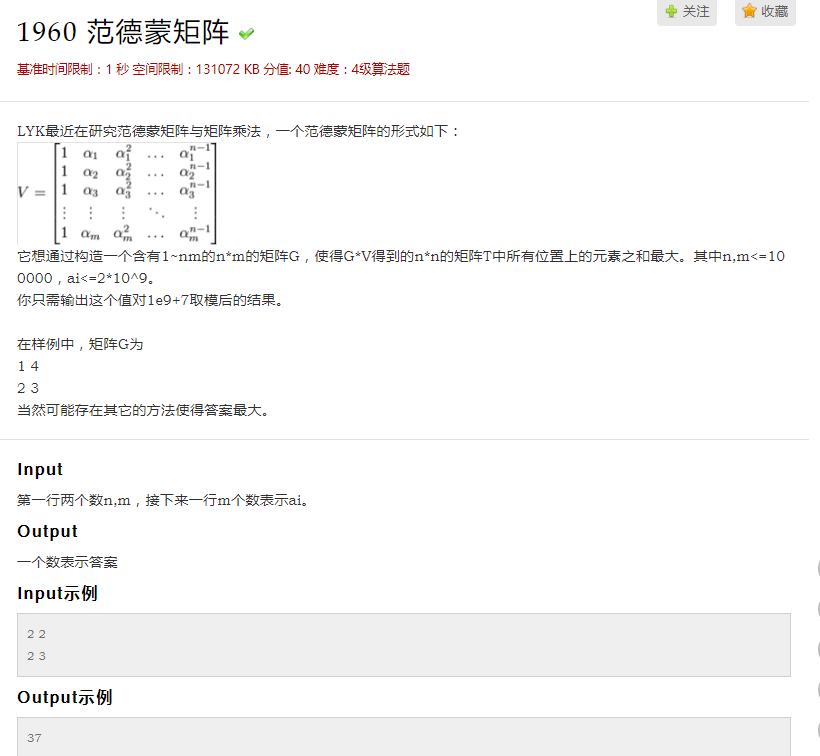
思路：　 根据矩阵乘法的定义，G中的第i行第j列的元素 ai,j ，对答案的贡献为 ai,j∗ T中第j行的所有元素之和。

　　　　因此我们可以将T中根据每行的和进行排序。第i行的和可以通过公式 (ai^n−1)/(ai−1)直接得出。
　　　　注意考虑 ai=1,ai=0 以及 ai>MOD 的特殊情况即可。还有就是对于除法取模需要用到逆元（费马小定理）

　　　　一开始没注意除法取模 狂WA 12遍也是心累。。。。。

 #include<iostream>
 #include<algorithm>
 #include<cstring>
 #include<cmath>

 using namespace std;
 typedef long long LL;
 const LL mod = 1e9 + ;
 const int maxn = 1e5 + ;
 LL b[maxn], ans, a[maxn];
 LL n, m;
 LL Pow(LL a, LL b)//快速幂
 {
     LL ans = ;
     while (b) {
         if (b & ) {
             ans *= a;ans %= mod;
         }
         a *= a;a %= mod;
         b >>= ;
     }
     return ans;
 }
 int main()
 {
     ios::sync_with_stdio(false);
     while (cin >> n >> m) {
         for (int i = ; i <= m; i++) {
             cin >> a[i];
         }
         sort(a + , a + m + );
         for (int i = ; i <= m; i++) {
             a[i] = (a[i] % mod + mod) % mod;
             if (a[i] == )b[i] = ;
             else if (a[i] == )b[i] = n;
             else {                            //费马小定理对除法取模
                 b[i] = (Pow(a[i], n) -  + mod) % mod;
                 b[i] = b[i] * Pow(a[i] - , mod - ) % mod;
             }
         }
         //以下是求解
         ans = ;
         LL num = (n*(n + ) / ) % mod;
         for (int i = ; i <= m; i++) {
             ans = (ans + (num*b[i]) % mod) % mod;
             num = (num + n * n) % mod;
         }
         cout << ans << endl;
     }
     return ;
 }