Codeforce 515A - Drazil and Date

Someday, Drazil wanted to go on date with Varda. Drazil and Varda live on Cartesian plane. Drazil's home is located in point (0, 0) and Varda's home is located in point (a, b). In each step, he can move in a unit distance in horizontal or vertical direction. In other words, from position (x, y) he can go to positions (x + 1, y), (x - 1, y), (x, y + 1) or (x, y - 1).

Unfortunately, Drazil doesn't have sense of direction. So he randomly chooses the direction he will go to in each step. He may accidentally return back to his house during his travel. Drazil may even not notice that he has arrived to (a, b) and continue travelling.

Luckily, Drazil arrived to the position (a, b) successfully. Drazil said to Varda: "It took me exactly s steps to travel from my house to yours". But Varda is confused about his words, she is not sure that it is possible to get from (0, 0) to (a, b) in exactly s steps. Can you find out if it is possible for Varda?

Input

You are given three integers a, b, and s ( - 109 ≤ a, b ≤ 109, 1 ≤ s ≤ 2·109) in a single line.

Output

If you think Drazil made a mistake and it is impossible to take exactly s steps and get from his home to Varda's home, print "No" (without quotes).

Otherwise, print "Yes".

Examples

input

5 5 11

output

No

input

10 15 25

output

Yes

input

0 5 1

output

No

input

0 0 2

output

Yes

Note

In fourth sample case one possible route is: .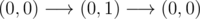

题解：记得加绝对值

 #include <iostream>
 #include <algorithm>
 #include <cstring>
 #include <cstdio>
 #include <vector>
 #include <cstdlib>
 #include <iomanip>
 #include <cmath>
 #include <ctime>
 #include <map>
 #include <set>
 using namespace std;
 #define lowbit(x) (x&(-x))
 #define max(x,y) (x>y?x:y)
 #define min(x,y) (x<y?x:y)
 #define MAX 100000000000000000
 #define MOD 1000000007
 #define pi acos(-1.0)
 #define ei exp(1)
 #define PI 3.141592653589793238462
 #define INF 0x3f3f3f3f3f
 #define mem(a) (memset(a,0,sizeof(a)))
 typedef long long ll;
 const int N=;
 const int mod=1e9+;
 int main()
 {
     ll a,b,s;
     while(cin>>a>>b>>s){
         a=llabs(a),b=llabs(b);
         int flag=;
         if(a+b>s) flag=;
         else {
             if(a+b==&&s%==) flag=;
             else if(a+b==&&s%==) flag=;
             else {
                 ll t=s-(a+b);
                 if(t%==) flag=;
                 else flag=;
             }
         }
         if(flag) cout<<"Yes"<<endl;
         else cout<<"No"<<endl;
     }
     return ;
 }