c++算法：计算行列式的值（详细讲解）

参考了：https://blog.csdn.net/u011885865/article/details/42032229

需要的基础：学过《线性代数》，知道行列式值的求法

基本公式：对于如下的行列式：

其值为：

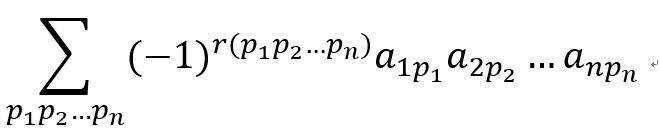
相信大家都懂这个公式的具体含义，我就不解释了，不懂的同学百度一下行列式

分析一个这个公式该如何实现：

假定现有有一个3*3的行列式，则其计算公式为：

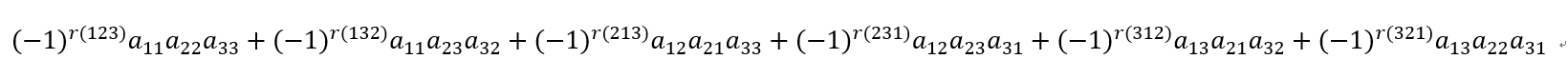
观察这个式子，可以发现其有一个核心，那就是生成一个全排列。本例中是一个3*3矩阵，因此需要生成123的全排列，共有六个：123、132、213、231、321、312。

然后就是要计算，生成的排列的逆序数，即

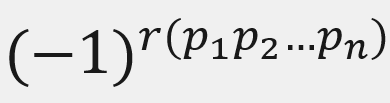
总结起来可分为如下几步：

1、求出给定n阶矩阵的全排列，我用vector<int>存储一个全排列（即上例中6个全排列中的某一个），用vector<vector<int> >存储所有的全排列（即上例中的六个全排列）。

2、计算排列的逆序数。

3、分别以1，2...n为row值，从vector<int>中依次提取的值为col值，组成行列式中元素的下标，然后相乘

4、求和。

算法实现：

1、求全排的算法如下，不懂该算法的可以移步：https://www.cnblogs.com/XiaoXiaoShuai-/p/10383535.html

//交换元素
void swap(vector<int>& vec, int i, int j)
{
	int temp = vec[i];
	vec[i] = vec[j];
	vec[j] = temp;
}

//第一个参数表示初始的数列，在上例中，该vec中的元素为1，2，3
//第二个参数表示最终得到的全排列集合
void Perm(vector<int>& vec, vector<vector<int> >& vec_seq, int current_index = 0)
{
	if (current_index == ((int)vec.size() - 1))
	{
		vec_seq.push_back(vec);
	}
	else
	{
		for (int i = current_index; i < (int)vec.size(); i++)
		{
			swap(vec, i, current_index);
			Perm(vec, vec_seq, current_index + 1);
			swap(vec, i, current_index);
		}
	}
}

　当然，还得有一个生成初始数列的函数

//根据n生成一个初始vector
vector<int> inivec(int n)
{
	vector<int> vec;
	for (int i = 0; i < n; i++)
		vec.push_back(i);
	return vec;
}

　第二步：求出全排列的逆序数，判断逆序数的奇偶

//得出排列的逆排序数，并根据奇偶判读正负
bool Iseven(int num)
{
	//用位与运算来判断奇偶（最快的判断奇偶的方法）
	return ((num & 1) == 0);
}
//是否幂为正
bool PowerIsPosition(vector<int>& vec)
{
	//count即为逆序数，初始化为0
	int count = 0;
	for (int i = 0; i < (int)vec.size(); i++)
	{
		for (int j = i + 1; j < (int)vec.size(); j++)
		{
			if (vec[i] > vec[j])
			{
				count += 1;
			}
		}
	}
	return (Iseven(count));
}

　　第三步和第四步：

//计算结果
//第一个参数表示输入的行列式
//第二个参数表示该行列式的阶数，在本例中n = 3，即一个3*3的行列式
int calculate(int** array, int n)
{
	vector<vector<int> > vec_que;
	vector<int> vec = inivec(n);
	vector<int> vec_elem;
	Perm(vec, vec_que);
	//最终结果，初始化为0
	int result = 0;
	//依次为vec_que中取出行列式
	for (int i = 0; i < (int)vec_que.size();i++)
	{
		vec_elem = vec_que[i];
		//mi即为前面(-1)的n次幂，最后结果为-1或者1
		int mi = PowerIsPosition(vec_elem) ? 1 : (-1);
		int temp = mi;
		//row号初始化为0之后依次加1
		int row = 0;
		//col号依次从vec_elem中取出
		for (int j = 0; j < (int)vec_elem.size();j++)
		{
			int col = vec_elem[j];
			temp *= array[row++][col];
		}
		result += temp;
	}
	return result;
}

　　检验一下：

int main()
{
	int** array = new int*[3];
	for (int i = 0; i < 3; i++)
	{
		array[i] = new int[3];
	}
	array[0][0] = 2;
	array[0][1] = -4;
	array[0][2] = 1;
	array[1][0] = 1;
	array[1][1] = -5;
	array[1][2] = 3;
	array[2][0] = 1;
	array[2][1] = -1;
	array[2][2] = 1;
	int result = calculate(array, 3);
	return 0;
}

　　计算的result = -8，结果正确