矩阵matrix变换的用法（css3属性transform: matrix）

参数

2D矩阵的表示 matrix(a,b,c,d,e,f)，其中6个参数在矩阵的分布：

 ——     ——
| a  c	e |
| b	 d	f |
| 0	 0	1 |
 ——     ——

在CSS3中矩阵的原始值是这样的：

transform: matrix(1,0,0,1,0,0);

任意点（x,y,1）经过matrix变化为（ax+cy+e,bx+dy+f,1)

矩阵平移

matrix(1,0,0,1,e,f)

e： 矩阵x坐标平移值，正向平移e
f： 矩阵y坐标平移值，正向平移f

css3中方向，单位为px

	|
	|
--------->x
	|
	↓y

结论：平移只有跟e和f有关系，跟其他a,b,c,d没有关系，e对应x轴的平移，f对应y轴的平移，往正方向平移多少单位就加上多少单位，反之则减去多少个单位。

矩阵缩放

matrix(a,0,0,d,0,0)

a： 矩阵宽度缩放a倍，默认为1不缩放
d： 矩阵高度缩放d倍，默认为1不缩放

结论：缩放只有跟a和d有关系，跟其他数值都无关，a对应x轴缩放，d对应y轴缩放，缩放多少倍就乘以多少

矩阵旋转

matrix（cosθ，sinθ,-sinθ,cosθ,0,0);

sinθ和cosθ最大值为1 最小值为-1，当a b c f四个参数符合公式的规律是则为旋转

往顺时针方向旋转45°

a = cos45° = 0.707
b = sin45° = 0.707
c = -sin45° = -0.707
d = con45° = 0.707
matrix(0.707,0.707,-0.707,0.707,0,0);

往顺时针方向旋转90°

a = cos90° = 0
b = sin90° = 1
c = -sin90° = -1
d = con90° = 0
matrix(0,1,-1,0,0,0);

往顺时针方向旋转180°

a = cos180° = -1
b = sin180° = 0
c = -sin180° = 0
d = con180° = -1
matrix(0,1,-1,0,0,0);

结论：得知旋转的度数，根据用sin cos算出相应的值填写

矩阵拉伸

matrix(1,tanθ,tanθ,1,0,0)

b：矩阵以X轴做偏移，偏移后X轴和右边的角度Y°,tanY° = b的值 （左边不变，右边向Y正方向偏远）
c：矩阵以Y轴做偏移，偏移后Y轴和左边的角度X°,tanX° = c的值 （底边不变，顶边向X正方向偏远）

matrix(1,2,0,1,0,0)

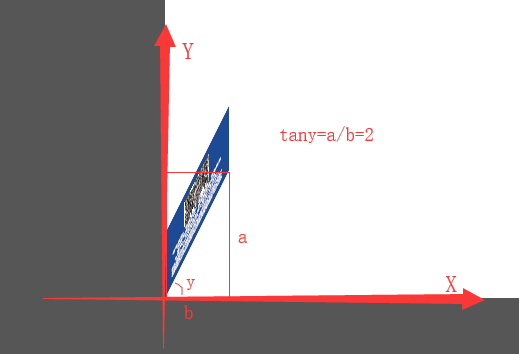
matrix(1,0,2,1,0,0)

参考

详细及原理请参考文章：

对CSS3中的transform：Matrix（）矩阵的一些理解
https://www.cnblogs.com/Ivy-s/p/6786622.html

理解CSS3 transform中的Matrix(矩阵)
https://www.zhangxinxu.com/wordpress/2012/06/css3-transform-matrix-%E7%9F%A9%E9%98%B5/