马尔科夫随机场(MRF)及其在图像降噪中的matlab实现

（Markov Random Field）马尔科夫随机场，本质上是一种概率无向图模型

下面从概率图模型说起，主要参考PR&ML 第八章 Graphical Model （图模型）

定义：A graph comprises nodes (also called vertices) connected by links (also known as edges or arcs ).

In a probilistic graphical model each node represents a random variable or group of random variables ,and th links express probabilistic  relationships between these variables.

分类：概率图模型大体分为两种，第一种是有向图，又叫贝叶斯网络，链接节点之间的边是有方向的，用来描述变量之间的因果关系（左侧）；另一种是无向图，又叫马尔科夫随机场，边是没有方向的，用来描述变量之间的软约束（右侧）。

1.Bayesian network

用概率图表示联合概率分布密度

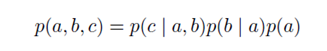
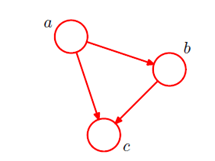
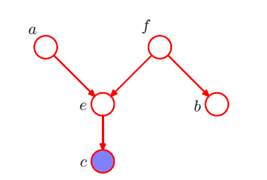
起点对应条件变量，如p(c|a,b)就会有两个起点一个终点。略微复杂一点如下图：

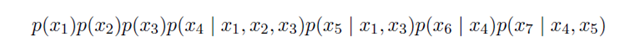
由于变量之间如果采用全连接会使得参数个数随着变量个数成幂次增加。所以书中讨论了几种在设计贝叶斯网络时减少模型参数的方法，第一种是独立性假设，即根据实际问题对某些变量提出独立性假设以减少链接边数；第二种是采用链式连接，即每个节点只有一个子节点一个父节点；第三种是权值共享，类似于cnn中底层的做法。

2 condition independence条件独立

定义式：

下面来讨论如何通过图结构直接判断变量之间的条件独立性

三个例子，一段总结

例一：结点c被称为关于（从a经过c到达b）这个路径的"尾到尾"（tail-to-tail）连接，因为结点与两个箭头的尾部相连

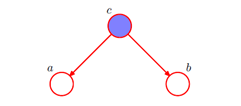
注意图中c是可观测变量

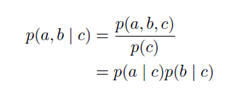
记作

例二：结点c被称为关于从结点a到结点b的路径"头到尾"（head-to-tail）。

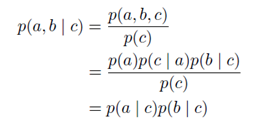
例三：结点c关于从a到b的路径是"头到头"（head-to-head），因为它连接了两个箭头的头。

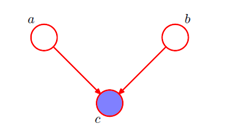
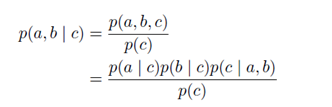
注意这里当c为观测条件时不能得到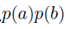的形式，所以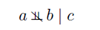

一个总结：In summary ,a tail-to-tail node or a head-to-tail node leaves a path unblocked unless it is observed in which case it blocks the path .By contrast, a head-to-head node blocks a path if it is unobserved ,but once the node ,and /or at least one of its descendants ,is observed the path becomes unblocked .参考译文（总而言之，TT结点或者HT结点形成的路径无堵，除非该结点被观察到（这会堵住路径）。相反，HH结点在没被观察到时会堵住路径，不过一旦该结点或其至少一个子结点被观察到的话，路径又变成无堵的了～）

一个小概念   D-separation：这个D-separaton的目的是通过有向无环图寻找一个特定的条件依赖表述 。针对节点（变量）集合，如果所有从A经过C到达B的路径都被阻隔，那么我们说C把A从B中d-separation.即

3.Markov Random Fields

一个马尔科夫随机场（Markov random field），也被称为马尔科夫网络（Markov network）或者无向图模型（undirected graphical model）（Kindermann and Snell, 1980），包含一组结点，每个结点都对应着一个变量或一组变量。链接是无向的，即不含有箭头。

这里同样来讨论他的独立性，集合A到集合B的所有路径都通过集合C中的一个或多个节点，那么所有这样的路径都被阻隔，因此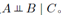或者说，除掉集合C之后A，B就没有连接路径了。

注意，只要有一条路径没有通过C，那么这种性质就不存在。

定义团块（clique）：对这个团块的所有子集的节点都是全连接的。

那么整个图的联合分布由各个团块组成，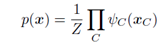

这里为每一个团块定义了一个势函数，注意如果这个无向图不是由有向图转化而来，那么这里的势函数可以不满足概率性质。但是，由于p(x)要满足概率性质，所以势函数还是要大于零的。Z是归一化因子。通常取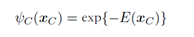这个分布叫做Boltzmann distribution（有时间要查查他的性质）。而这里最大的优势就是势函数可以通过选取而具有一定的实际意义，相当于一种相似度的度量，所以为算法的设计增加了灵活性。

例子：图像去噪

这个例子可以有很多更好的方法实现，这里只是为了说明势函数的用法而已。

给一幅二值图像加入噪声，加入噪声之后的图像是我们的观测值Y，而实际图像是隐变量X,现在我们就要通过Y推断X,

由于噪声等级比较小，因此我们知道xi和yi之间有着强烈的相关性。我们还知道图像中相邻像素xi和xj的相关性很强。这种先验知识可以使用马尔科夫随机场模型进行描述，它的无向图如下：

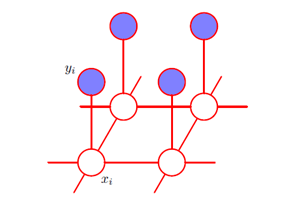
势函数定义为：

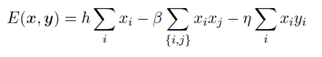
这里只有两种团块，第一种是xi和yi，第二种是xi和相邻的xj。我们分别给以不同系数用来调节其在势函数中的权重，由于最后的概率计算要取最大，所以这里等价于取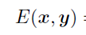最小。

具体代码如下：

%实现PRML P387 例子：使用mrf降噪
%输入一个二值图像并加入噪声
close all;
clear all;
I=imread('Penguins.jpg');
I1=im2bw(I);
subplot(2,2,1)
imshow(I1);
title('原图像');
J = imnoise(I,'salt & pepper', 0.2);
J1=im2bw(J);
subplot(2,2,2)
imshow(J1);
title('噪声图')

Y=ones(size(J1));
Y(J1==0)=-1;
[m,n]=size(Y);
X=Y;h=0;beta=3.5;eta=.1;
while 1
    tot=0
    for i=2:1:m-1
        for j=2:1:n-1
            temp=X(i,j);
            X(i,j)=-1;%根据定义计算势函数
        E1=h*X(i,j)-beta*X(i,j)*(X(i-1,j)+X(i+1,j)+X(i,j-1)+X(i,j+1))-eta*X(i,j)*Y(i,j);
           X(i,j)=1;
           E2=h*X(i,j)-beta*X(i,j)*(X(i-1,j)+X(i+1,j)+X(i,j-1)+X(i,j+1))-eta*X(i,j)*Y(i,j);
           if E1<E2
                X(i,j)=-1;
            else
                X(i,j)=1;
            end
            if temp~=X(i,j)
                tot=tot+1;
            end
        end
    end
    if tot<1
        break;
    end
end

J2=X;
J2(X==-1)=0;
subplot(2,2,3)
imshow(J2);
title('mrf降噪结果')

结果如下：