机器学习总结-bias–variance tradeoff

bias–variance tradeoff

通过机器学习，我们可以从历史数据学到一个\(f\)，使得对新的数据\(x\)，可以利用学到的\(f\)得到输出值\(f(x)\)。设我们不知道的真实的\(f\)为\(\overline{f}\)，我们从数据中学到的\(f\)为\(f^{*}\)，实际上\(f^{*}\)是\(\overline{f}\)的一个估计。在统计中，变量\(x\)的均值\(mean\)表示为\(\mu\)，方差\(variance\)表示为\(\sigma\)，假设我们抽取出\(x\)的\(N\)个样本，可以用\(m=\frac{1}{N}\sum_{i=1}^{N}x_{i}\)来估计\(\mu\)，但实际上\(m \neq \mu\)，如果我们抽取很多次得到不同的m，那么期望\(E(m)=E(\frac{1}{N}\sum_{i=1}^{N}x_{i})=\frac{1}{N}\sum_{i=1}^{N}E(x_{i})=E(x)=\mu\)。\(var(m)=\frac{\sigma^2}{N}\)，即抽取的样本\(N\)大，\(m\)的\(variance\)越小。\(s^2=\frac{1}{N}\sum_{i=1}^{N}(x_{i}-m)^2\)，\(E(s^2)=\frac{N-1}{N}\sigma^2\neq\sigma^2\)，因此\(s^2\)是有偏估计量。
实际上，如果用平方误差表示，误差分为3个部分（来自wikipedia）:

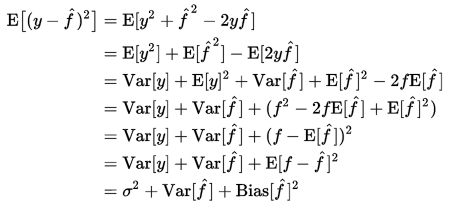
偏差度量了学习算法的期望预测与真实结果的偏离程度，即刻画了学习算法本身的拟合能力；
方差度量了同样大小的训练集的变动所导致的学习性能的变化，即刻画了数据扰动所造成的影响；
噪声则表达了在当前任务上任何学习算法所能达到的期望泛化误差的下界，即刻画了学习问题本身的难度。
通常，简单的模型variance小（不同数据上的结果差异较小），bias大，容易表现为欠拟合，需要增加模型复杂度，加入新的特征；复杂的模型variance大（表达能力强，对不同数据较敏感，结果差异较大），bias小（平均来说与真实结果较为接近），容易表现为过拟合，需要增加更多数据（非常有效，但不太现实）或者用正则化来控制模型的复杂程度。

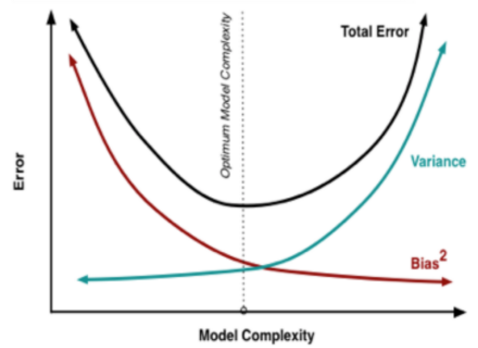
常见错误：
在机器学习任务中，如果使用测试集正确率为依据来调整模型，容易出现过拟合的现象，使得泛化误差很大。通常做法是交叉验证（Cross Validation），根据划分验证集上的平均结果来调整模型，不要过分关心测试集上的结果，如果验证集上的误差小，那么测试集上的期望误差也会小。