明文攻击（Known plaintext attack）：是一种攻击模式，指攻击者已知明文、密文及算法，求密钥的过程。

例题：

这就是一个坑

密码是十位大小写字母、数字、特殊符号组成的，你爆破的开么？！

key格式：flag{xxx}

解题链接：http://ctf5.shiyanbar.com/misc/no.zip

1、解压得 flag.zip 和 tips.txt，提示“密码是十位大小写字母、数字、特殊符号组成的，你爆破的开么？！”

这意味着爆破很难，用winhex分析，flag.zip 里有 flag.txt 和 tips.txt 两个文件

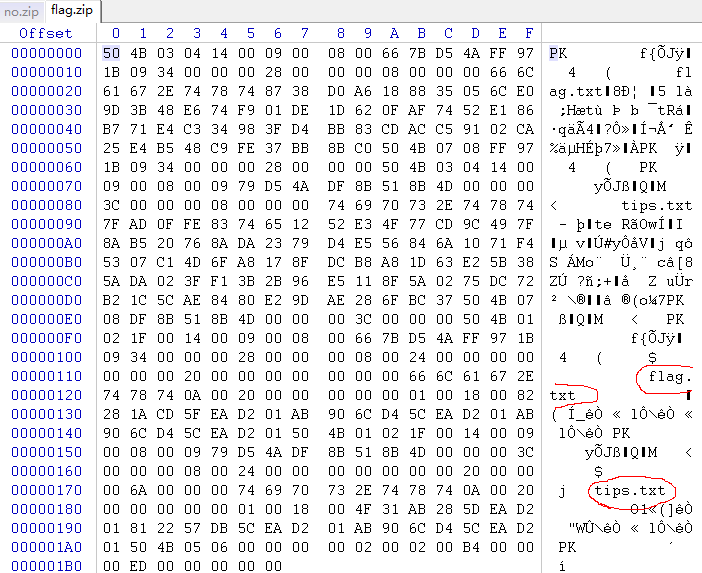
2、比较两个tips.txt是否为同一文件

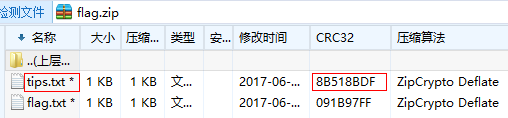
3、显然，已知未加密的 tips 和 flag.zip 里被加密后的 tips，又知是zip加密，故可用AZPR进行明文攻击

工具AZPR-4.0百度云分享         链接：http://pan.baidu.com/s/1qYVz6aS  密码：ixhe

----------------------------------------------------------------分割线---------------------------------------------------------

ps:萌新一枚，本文纯为学习笔记，以防某日犯傻忘记--。如有不妥处，望大佬们赐教~

密码学笔记——zip明文攻击的更多相关文章

  1. 密码学笔记——eval(function(p,a,c,k,e,d) 加密破解

    密码学笔记——eval(function(p,a,c,k,e,d) 的加密破解 例题: 小明某天在看js的时候,突然看到了这么一段代码,发现怎么也理不出代码逻辑,你能帮帮他吗? 格式:SimCTF{} ...

  2. 密码学笔记(5)——Rabin密码体制和语义安全性

    一.Rabin密码体制 Rabin密码体制是RSA密码体制的一种,假定模数$n=pq$不能被分解,该类体制对于选择明文攻击是计算安全的.因此,Rabin密码体制提供了一个可证明安全的密码体制的例子:假 ...

  3. 密码学笔记(2)——RSA密码

    上一篇笔记中讲述了大量的代数知识,这一篇中我们看看如何将这些代数知识应用到RSA密码体制中. 一.公钥密码学简介 在经典密码学的研究模型中,我们根据已选择的秘钥K得到一条加密规则$e_{k}$和一条解 ...

  4. 密码学笔记(4)——RSA的其他攻击

    上一篇详细分析了几种分解因子的算法,这是攻击RSA密码最为明显的算法,这一篇中我们考虑是否有不用分解模数n就可以解密RSA的密文的方法,这是因为前面也提到,当n比较大的时候进行分解成素数的乘积是非常困 ...

  5. 密码学笔记——playfair密码

     Playfair密码(Playfair cipher 或 Playfair square)一种替换密码,1854年由查尔斯·惠斯通(Charles Wheatstone)的英国人发明. 例题: 某种 ...

  6. 密码学笔记——Rot13

    Rot13:将每个在字母表上的字母,用后数13个后的字母代替,若超过时则重新绕回26字母开头即可. eg:A换成N.B换成O.依此类推到M换成Z,然后序列反转:N换成A.O换成B.最后Z换成M 1.密 ...

  7. 密码学系列之:明文攻击和Bletchley Park

    目录 简介 crib和明文攻击 布莱奇利公园(Bletchley Park) 简介 明文攻击就是指已经知道了部分明文和它对应的加密后的字段,从而可以推测出使用的加密手段或者密码本.明文攻击这个故事还要 ...

  8. 密码学笔记-一段base64wp

    CTF--练习平台 例题: 一段Base64 flag格式:flag{xxxxxxxxxxxxx} 附件: base64.txt 1.base64解码:http://base64.xpcha.com/ ...

  9. Python学习笔记第五周

    目录 一.基础概念 1.模块定义 2.包的定义 3.导入包的本质 4.导入模块的本质 5.导入方法 6.import的本质 7.导入优化 8.模块分类 9.标准库介绍 1.time与datetime ...

随机推荐

  1. Winform中怎样对窗体进行隐藏，再次打开时仍然保留上次的窗体

    场景 点击按钮后打开窗口,点击窗口的确定按钮后即使窗体返回了Ok,此时不关闭窗体,将窗体隐藏. 再次点击按钮后,仍然打开上次的窗体. 注: 博客主页: https://blog.csdn.net/ba ...

  2. springboot web - 建立路由

    一. 测试代码 @RestController @RequestMapping("/book") public class BookController { @PostMappin ...

  3. 2020.01.19【NOIP提高组】模拟比赛-1.水池,2.数字排序,3.球星,4.钻石交易 总结反思

    水池 比赛时 我最讨厌这种数学类题了,我首先想到了这几种情况,设\(jl[][]\)表示两点之间弧的距离,从F到G可以由 F->G F->B->A->G F->A-> ...

  4. CF575A Fibonotci [线段树+矩阵快速幂]

    题意 \(s\{\}\) 是一个循环数列 循环节为 \(n\),你可以改掉 \(m\) 项,这 \(m\) 项独立,且不影响循环节 考虑线段树维护矩阵,单点修改最多m次,每次矩阵快速幂就完事了 // ...

  5. 查看whl包名是否满足系统的条件的命令，以此解决whl包出现“is not a supported wheel on this platform”错误提示的问题

    在Ubuntu系统中,使用pip安装whl包时,常常会报如下错误: tensorflow_gpu-1.11.0-cp35-cp35m-manylinux1_x86_64.whl is not a su ...

  6. commons-dbutils实现增删改查

    1.maven依赖 <?xml version="1.0" encoding="UTF-8"?> <project xmlns="h ...

  7. Agri-Net POJ - 1258 prim

    #include<iostream> #include<cstdio> #include<cstring> using namespace std; ; #defi ...

  8. 指数函数在c语言实现

    指数很重要,比如有一些欧拉公式 #include "common.h" #include <stdio.h> #include <stdlib.h> #in ...

  9. Wannafly Winter Camp 2020 Day 5G Cryptographically Secure Pseudorandom Number Generator - 分块

    多组数据,给定质数 \(p\) ,求所有 \(x\) 使得 \(f(x)=\min_{k=2}^x f(k)\) ,其中 \(f(x)=x^{-1}\) 所有 \(p\) 在 \([1,10^9]\) ...

  10. python3包、模块、类、方法的认识

    包>>模块>>类>> 函数 包:就是一个目录,import time from+import导入包中的部分模块 直接到类 from budaoguan.common ...