「洛谷P1231」教辅的组成 解题报告

P1231 教辅的组成

题目背景

滚粗了的HansBug在收拾旧语文书，然而他发现了什么奇妙的东西。

题目描述

蒟蒻HansBug在一本语文书里面发现了一本答案，然而他却明明记得这书应该还包含一份练习题。然而出现在他眼前的书多得数不胜数，其中有书，有答案，有练习册。已知一个完整的书册均应该包含且仅包含一本书、一本练习册和一份答案，然而现在全都乱做了一团。许多书上面的字迹都已经模糊了，然而HansBug还是可以大致判断这是一本书还是练习册或答案，并且能够大致知道一本书和答案以及一本书和练习册的对应关系（即仅仅知道某书和某答案、某书和某练习册有可能相对应，除此以外的均不可能对应）。既然如此，HansBug想知道在这样的情况下，最多可能同时组合成多少个完整的书册。

输入输出格式

输入格式：

第一行包含三个正整数N1、N2、N3，分别表示书的个数、练习册的个数和答案的个数。

第二行包含一个正整数M1，表示书和练习册可能的对应关系个数。

接下来M1行每行包含两个正整数x、y，表示第x本书和第y本练习册可能对应。（$1 \le x \le N1，1\le y\le N2 $）

第M1+3行包含一个正整数M2，表述书和答案可能的对应关系个数。

接下来M2行每行包含两个正整数x、y，表示第x本书和第y本答案可能对应。（\(1 \le x \le N1，1 \le y \le N3\)）

输出格式：

输出包含一个正整数，表示最多可能组成完整书册的数目。

输入输出样例

输入样例#1：

5 3 4
5
4 3
2 2
5 2
5 1
5 3
5
1 3
3 1
2 2
3 3
4 3

输出样例#1：

2

说明

样例说明：

如题，N1=5，N2=3，N3=4，表示书有5本、练习册有3本、答案有4本。

M1=5，表示书和练习册共有5个可能的对应关系，分别为：书4和练习册3、书2和练习册2、书5和练习册2、书5和练习册1以及书5和练习册3。

M2=5，表示数和答案共有5个可能的对应关系，分别为：书1和答案3、书3和答案1、书2和答案2、书3和答案3以及书4和答案3。

所以，以上情况的话最多可以同时配成两个书册，分别为：书2+练习册2+答案2、书4+练习册3+答案3。

数据规模：

对于数据点1, 2, 3，\(M1，M2\le 20\)

对于数据点4~10，\(M1，M2 \le 20000\)

---

算法

网络最大流。这里不详细讲，请大家先掌握。

思路

注意，以下出现的所有边边权皆为1，且其反向边边权为0

我们以书、练习册、答案为点建图。

像这样：

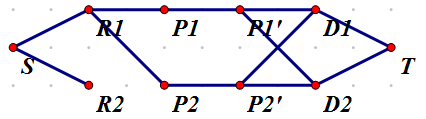
S(=0)表示额外建的一个起始点，Ri(=i+N1+N1)表示第i本练习册，Di(=i+N1+N1+N2)表示第i本答案，由于书只有一本，而网络流处理只经过一个点不方便，我们采用一种神奇方法——拆点！也就是说，把一本书看做两个点，要匹配这本书必须经过这本书两点之间的边，这样就可以控制这本书只匹配一次。如图，Pi(=i)、Pi'(=i+N1)表示第i本书。

然后建边。如图，将S与所有Ri相连，将所有的Di与T相连，S作为源点，T作为汇点。如果Pi能匹配Rj，就将Pi与Rj相连。如果Pi能匹配Dj，就将Dj与Pi'之间相连。当然，Pi与Pi'之间也要连一条边。

然后就可以套网络最大流辣。最后得出的答案即为最多的数目。

代码

#include<bits/stdc++.h>
using namespace std;
#define open(s) freopen( s".in", "r", stdin ), freopen( s".out", "w", stdout )
#define MAXN 40005
#define MAXM 150000

int N1, N2, N3;
int M1, M2;
int hd[MAXN], nxt[MAXM << 1], to[MAXM << 1], val[MAXM << 1], tot(1);
int ans, dis[MAXN];
queue<int> Q;
bool vis[MAXN];

int x, y;
int S, T;

void Add( int x, int y, int z ){ nxt[++tot] = hd[x]; hd[x] = tot; to[tot] = y; val[tot] = z; }

bool BFS(){
	while( !Q.empty() ) Q.pop();
	memset( dis, 0, sizeof dis );
	Q.push(S); dis[S] = 1;
	while( !Q.empty() ){
		x = Q.front(); Q.pop();
		for ( int i = hd[x]; i; i = nxt[i] )
			if ( val[i] && !dis[to[i]] ){
				dis[to[i]] = dis[x] + 1;
				Q.push( to[i] );
				if ( to[i] == T ) return 1;
			}
	}
	return 0;
}

int DFS( int x, int fl ){
	if ( x == T ) return fl;
	int res(fl), k;
	for ( int i = hd[x]; i && res; i = nxt[i] ){
		if ( val[i] && dis[to[i]] == dis[x] + 1 ){
			k = DFS( to[i], min( res, val[i] ) );
			if ( !k ) dis[to[i]] = 0;
			val[i] -= k; val[i^1] += k; res -= k;
		}
	}
	return fl - res;
}

int main(){
	scanf( "%d%d%d", &N1, &N2, &N3 );
	scanf( "%d", &M1 );
	for ( int i = 1; i <= M1; ++i ){
		scanf( "%d%d", &x, &y ); Add( y + N1, x, 1 ); Add( x, y + N1, 0 );
	}
	scanf( "%d", &M2 );
	for ( int i = 1; i <= M2; ++i ){
		scanf( "%d%d", &x, &y ); Add( x + N1 + N2 + N3, y + N1 + N2, 1 ); Add( y + N1 + N2, x + N1 + N2 + N3, 0 );
	}
	S = 0; T = 1 + N1 + N1 + N2 + N3;
	for ( int i = 1; i <= N2; ++i ) Add( S, i + N1, 1 ), Add( i + N1, S, 0 );
	for ( int i = 1; i <= N3; ++i ) Add( i + N1 + N2, T, 1 ), Add( T, i + N1 + N2, 0 );
	for ( int i = 1; i <= N1; ++i ) Add( i, i + N1 + N2 + N3, 1 ), Add( i + N1 + N2 + N3, i, 0 );

	int t;
	while( BFS() )
		while( ( t = DFS( S, 0x7f7f7f7f ) ) > 0 ) ans += t;
	printf( "%d\n", ans );
	return 0;
}