2019牛客多校第八场 F题 Flowers 计算几何+线段树

2019牛客多校第八场 F题 Flowers

先枚举出三角形内部的点D。

下面所说的旋转没有指明逆时针还是顺时针则是指逆时针旋转。

固定内部点的答案的获取

anti(A)anti(A)anti(A)或者说A‾\overline{A}A表示DA→\overrightarrow{DA}DA旋转180°之后的方向。

block(A,B)block(A,B)block(A,B)表示的是DA→\overrightarrow{DA}DA旋转到DB→\overrightarrow{DB}DB的扫过的几何区间。小括号表示不包含边界，中括号表示包含边界。

假设确定了A点，那么对于D,A的ans数是

∑B∈(A,A‾)∑C∈(A‾,B‾)1\sum\limits_{B \in (A,\overline{A})}\sum\limits_{C \in (\overline{A}, \overline{B})}1B∈(A,A)∑​C∈(A,B)∑​1.

以下是示意图。对于一个确定的A，B在蓝色区间范围内取一个点。

之后对于确定的B，C只需要且只能在绿色区间范围选一个。

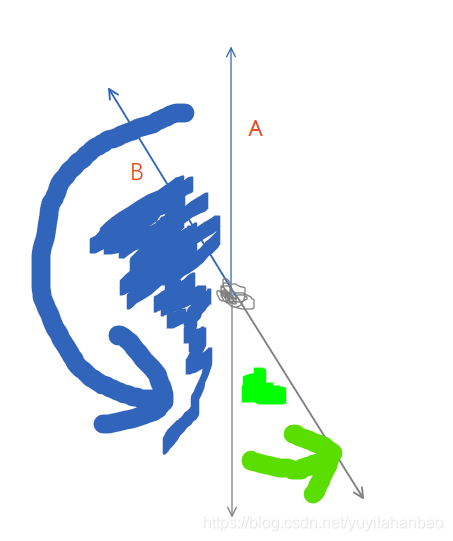
如何确定几何区间里点的个数呢？

我们可以先求出一下信息保存在数组中。

1. 各个点按逆时针方向编号
2. 各个点的方向dir数组
3. 各个方向第一个点的编号和最后一个点的编号，即firstfirstfirst和lastlastlast.infos数组
4. 各个方向的反向方向的firstfirstfirst和lastlastlast.antiinfos数组.

假设我们都已经求出来了。

∑B∈(A,A‾)∑C∈(A‾,B‾)1=∑B∈(A,A‾)antiinfos[dir[B]].first−antiinfos[dir[A]].last−1\sum\limits_{B \in (A,\overline{A})}\sum\limits_{C \in (\overline{A}, \overline{B})}1\\
=\sum\limits_{B \in (A,\overline{A})}antiinfos[dir[B]].first - antiinfos[dir[A]].last - 1B∈(A,A)∑​C∈(A,B)∑​1=B∈(A,A)∑​antiinfos[dir[B]].first−antiinfos[dir[A]].last−1

而B∈(A,A‾)B \in (A,\overline{A})B∈(A,A)换成点的编号表示的话就是——

infos[dir[A]].last+1≤B&lt;antiinfos[dir[A]].first&ThickSpace;infos[dir[A]].last + 1 \leq B &lt; antiinfos[dir[A]].first\;infos[dir[A]].last+1≤B<antiinfos[dir[A]].first

注意现在的求和式中对于一个固定的A来说，有关A的都是常量。所以这是一个只和变量B有关的式子。

所以可以看做对一个数组a[B]a[B]a[B]求区间和的式子。

即变成∑B=infos[dir[A]].last+1antiinfos[dir[A]].first−1a[B]\sum\limits_{B = infos[dir[A]].last + 1}^{antiinfos[dir[A]].first - 1} a[B]B=infos[dir[A]].last+1∑antiinfos[dir[A]].first−1​a[B].

对于一个固定的A求出每一个a[B]只能对一个个B单独求.

但AAA换成下一个方向的A′A'A′时。B的上界和下界将会随之改变，但是新的上界和下界，很有可能会有一大段重复的。即假设旧的区间是[l,r],新的区间是[L,R]。对于这两个区间重叠的部分B∈[u,v]B \in [u,v]B∈[u,v].对于a[B]来讲，B没有变化，变化的只是A变成了A’。所以[u,v][u,v][u,v]区间里的a[B]a[B]a[B]只需要在集体区间减去一个与A,A′A,A'A,A′有关的变化量即可。而对于[L,R]区间中不重叠的部分，就只能一个一个B单独枚举计算了。由于A是从逆时针方向一个个往后枚举的，所以上下界[l,r]也是一直往后移动。因此，不重叠的需要单独计算的部分a[B]最多就是每个点计算一次。对于所有的A来说，单独计算修改次数是O(n)O(n)O(n)级别的。求区间和的次数也是O(n)O(n)O(n)级别的。

因此可以使用线段树解决。

注意

对于一朵Flower ABC-D，D是内部点，在这个方法下，会被计算三次。分别是A，B，C充当上面所说的A点。所以最后答案要除以3.

反向信息的求取

对于旋转180°之后的方向，即反方向。如果这个方向上有点，那么就取这个方向的firstfirstfirst和lastlastlast;如果这个方向上没有点，那么firstfirstfirst置为旋转度数超过180°的第一个方向的firstfirstfirst,而lastlastlast就是first−1first-1first−1。

对于单个方向DP→\overrightarrow{DP}DP的反方向的DP→‾\overline{\overrightarrow{DP}}DP显然可以通过DP→\overrightarrow{DP}DP的以下一个方向开始，一个个方向检查过去，找到恰好180°或者第一个大于180°的。因此复杂度是O(n)O(n)O(n)

---

对于P所有方向的反方向是O(n2)O(n^2)O(n2)???

由于我们一个点P的方向实际上是DP→\overrightarrow{DP}DP的方向，所以外面还有一层枚举D的O(n)O(n)O(n).那样子O(n3)O(n^3)O(n3)就Tle了。

---

但是，注意到DP→\overrightarrow{DP}DP的下一个方向DQ→\overrightarrow{DQ}DQ​的反向DQ→‾\overline{\overrightarrow{DQ}}DQ​​，肯定不会早于DP→‾\overline{\overrightarrow{DP}}DP出现。所以可以整体O(n)O(n)O(n)。求出所有方向的反向。

最后总的复杂度是

O(n^2lnn).

其中排序、线段树的区间查询、修改都达到了O(n^2lnn)。

###　源程序

代码中的区间l,r,L,R是左闭右开的。first和last则都是包含的。

#include <bits/stdc++.h>
using namespace std;
typedef long long ll;

//#define debugmode

const int kMaxPointCount = 1024;
const int kMaxPointCount2 = kMaxPointCount*2;
struct nd{
    int l,r;
    ll all_add, sum;
};
nd nds[kMaxPointCount2<<2];
inline int lchild(int x) { return (x << 1) | 1;}

void build(int l,int r,int root = 0) { // 针对本题特殊定制的build
    nds[root].l = l; nds[root].r = r;
    nds[root].all_add = 0; nds[root].sum = 0;
    if (l + 1 == r) return;
    int m = l + (r - l) / 2;
    int lch = lchild(root);
    build(l, m, lch);
    build(m, r, lch+1);
}

void add(int l, int r, ll val, int root = 0) {
    if (l == nds[root].l && r == nds[root].r) {
        nds[root].all_add += val;
        // sum是不考虑自己的以及祖先的all_add的flag情况下的sum
        // 所以这个节点区间集体加的时候不update sum
        return;
    }
    int m = (nds[root].l + nds[root].r)/2;
    int lch = lchild(root);
    if (r <= m) {  // only left part
        add(l, r, val, lch);
    } else if (l >= m) {  // only right part
        add(l, r, val, lch+1);
    } else {
        add(l, m, val, lch);
        add(m, r, val, lch+1);
    }
    // merge_flags
    // sum是不考虑自己的以及祖先的all_add的flag情况下的sum
    nds[root].sum += val * (r-l);
}

ll get_sum(int l, int r, int root = 0) {
    ll base = nds[root].all_add*(r-l); // 求和函数需要把all_add标记考虑到（修正）
    if (l == nds[root].l && r == nds[root].r) {
        return nds[root].sum + base;
    }
    int m = (nds[root].l + nds[root].r)/2;
    int lch = lchild(root);
    if (r <= m) {  // only left part
        return get_sum(l, r, lch) + base;
    } else if (l >= m) {  // only right part
        return get_sum(l, r, lch+1) + base;
    } else {
        return get_sum(l, m, lch) + get_sum(m, r, lch+1) + base;
    }
}
struct point_with_angle;
struct point{
  ll x, y;
    point(){}
    point(ll x, ll y):x(x),y(y) {}
  void set(const point_with_angle& a);
    ll operator *(const point&b) const {return x*(ll)b.x+y*b.y;} // 向量积，点积
    ll operator %(const point&b) const {return x*(ll)b.y-y*b.x;} // 叉乘
    point operator -(const point &b) const {return point(x - b.x, y-b.y);}
    point operator +(const point &b) const {return point(x + b.x, y+b.y);}
    bool operator ==(const point&b) const {return x == b.x && y == b.y;}
};
inline int sign(ll a) {return a ? (a > 0 ? 1 : -1) : 0;}

struct point_with_angle {
  ll x, y;
  int type;
	double k;
  void set(const point& a) {
    x = a.x; y = a.y;
    if (y < 0) type = 0;
		else if (y > 0) type = 2;
		else if (x > 0) type = 1;
		else type = 3;
		if (type & 1) k = x;
		else k = x/(double)y;
  }
  bool operator<(point_with_angle& b) const {
		if (type != b.type)
			return type < b.type;
		else
			return k > b.k;
	}
};

void point::set(const point_with_angle& a)  {x = a.x; y = a.y;}

struct info{
    int first,last,cnt;
    info(){}
    void set(int f, int l) {first = f; last = l; cnt = l-f+1;}
};

point inp[kMaxPointCount];
typedef point vec;
point_with_angle sort_p[kMaxPointCount];
vec vecs[kMaxPointCount2];
int vec_to_dir[kMaxPointCount2];
// infos of dir and infos of anti dir
info infos[kMaxPointCount2],antiinfos[kMaxPointCount2];
int pn, vecn, dirn;

void get_vecs(int d) {
    vecn = 0;
    for (int i = 0; i < pn; ++i)
        if (inp[i] == inp[d]) continue;
        else sort_p[vecn++].set(inp[i]-inp[d]);
    sort(sort_p, sort_p+vecn);
    for (int i = 0; i < vecn; ++i)
        vecs[i].set(sort_p[i]);
    for (int i = 0, j = vecn; i < vecn; ++i, ++j)
        vecs[j] = vecs[i];
}

// a,b都是非零向量
bool is_same_dir(const vec&a, const vec&b) { return a%b == 0 && a*b > 0; }

void get_dir() {
    // 如果和前面的方向相同，那么就应该用前面的dir
    // 否则，应该使用新dir
    dirn = 0;
    for (int i = 0; i < vecn; ++i) {
        if (i && is_same_dir(vecs[i],vecs[i-1])) {
            vec_to_dir[i] = dirn - 1;
        } else {
            ++dirn;
            vec_to_dir[i] = dirn - 1;
        }
    }
    for (int i = 0, j = vecn; i < vecn; ++i, ++j)
        vec_to_dir[j] = vec_to_dir[i] + dirn;
}

void get_infos() {
    for (int i = 0, d = -1; i < vecn; ++i) {
        if (vec_to_dir[i] != d) {
            if (d >= 0) infos[d].last = i-1;
            d = vec_to_dir[i];
            infos[d].first = i;
        }
    }
    if (dirn) infos[dirn -1].last = vecn - 1;
    for (int i = 0; i < dirn; ++i)
        infos[i].cnt = infos[i].last - infos[i].first + 1;
    for (int i = 0, j = dirn; i < dirn; ++i, ++j)
        infos[j].set(infos[i].first + vecn, infos[i].last + vecn);
}

void get_antiinfos() {
    // j应该在anti(i)的位置停下，如果有的话。如果没有的话，
    // 那么它停在的是逆时针旋转超过180°的第一个存在的vec
    // j的探查范围开始是i后一个方向 止于i旋转一圈的方向i+dirn（不含）
    // 因为判断逆时针旋转度数只是单纯的使用叉乘
    // 叉乘为0视作旋转180°，＜0旋转小于180°，>0旋转大于180°
    // 如果不对j做限定，将会同一个方向视作旋转180°
    int i,j;
    int res;
    for (i = 0, j = 0; i < dirn; ++i) {
        for (j = max(j, i+1); j < i + dirn; ++j) {
            res = sign(vecs[infos[i].first]%vecs[infos[j].first]);
            if (res == 0) { // = 180°
                antiinfos[i].set(infos[j].first, infos[j].last);
                break;
            } else if (res < 0) { // > 180°
                antiinfos[i].set(infos[j].first, infos[j].first -1);
                break;
            }
        }
        if (j >= i + dirn) {
            antiinfos[i].set(infos[j].first, infos[j].first -1); // 360°
        }
    }
    for (int i = 0, j = dirn; i < dirn; ++i, ++j)
        antiinfos[j].set(antiinfos[i].first + vecn, antiinfos[i].last + vecn);
}

ll solve() {
    ll ans = 0;
    int dA, dB;
    int B;
    int l = 0, r = 0, L, R;
    bool need_work;
    ll tmp_val;
    build(0, 2 * vecn);
    for (dA = 0; dA < dirn; ++dA) {
        L = infos[dA].last + 1;
        R = antiinfos[dA].first;
        need_work = L < R;
        if (need_work && L < r) {
            // 区间集体减
            tmp_val = antiinfos[dA].last - antiinfos[dA-1].last;
            add(L, r, -tmp_val);
        }
        for (B = max(L, r); B < R; B = infos[dB].last + 1) {
            dB = vec_to_dir[B];
            add(B, infos[dB].last + 1,
                antiinfos[dB].first - antiinfos[dA].last - 1);
        }
        if (need_work) {
            tmp_val = get_sum(L, R);
            ans += infos[dA].cnt * tmp_val;
        }
        l = L; r = R;
    }
    return ans;
}

int main() {
    cin>>pn;
    for (int i = 0; i < pn; ++i)
        scanf("%lld%lld",&inp[i].x, &inp[i].y);
    ll ans = 0;
    for (int d = 0; d < pn; ++d) {
        get_vecs(d);
        get_dir();
        get_infos();
        if (dirn < 3) continue;
        get_antiinfos();
        ans += solve();
    }
    cout<<ans/3<<endl;
    return 0;
}

弱鸡的我的吐槽模块

由于一开始按照逆时针编号的排序是使用atan2获取极角，然后一直卡在90.48%。各个地方都改过，还是一直过不去。写了两天了，这个程序还是推倒然后重新写的一个。

debug到怀疑人生。最后发现牛客网提交的程序里面可以有assert语句，然后，assert不成立还会re并提示是哪一行assert语句出错了。

于是疯狂assert。

通过疯狂assert最后诡异的发现更后面的anti的last居然比前面的last还要小，导致区间集体要减去的数算出来是个负数。

然后疯狂读自己的程序，妄图找出bug，分析了好久好久，分析到最后已经相当于从数学上确定，没有逻辑错误，就是正确的。

想过爆long long。但是想来想去不可能，许久之后怀疑是排序之后并不是逆时针排列的，最后把atan2换掉了之后，突然就ac了。

atan2让我浪费了一天半的时间。

珍爱生命，慎用atan2.

感觉最近队内输出基本都是靠lsq输出，疯狂白嫖队友的感觉。

羞愧.jpeg