【中文分词】最大熵马尔可夫模型MEMM

Xue & Shen '2003 [2]用两种序列标注模型——MEMM (Maximum Entropy Markov Model)与CRF (Conditional Random Field)——用于中文分词；看原论文感觉作者更像用的是maxent (Maximum Entropy) 模型而非MEMM。MEMM是由McCallum et al. '2000 [1]提出MEMM，针对于HMM的两个痛点：一是其为生成模型（generative model），二是不能使用更加复杂的feature。

1. 前言

首先，将简要地介绍HMM与maxent模型。

HMM

概率图模型（probabilistic graphical model, PGM）指用图表示变量相关（依赖）关系的概率模型，主要分为两类：

• 有向图模型或贝叶斯网（Bayesian network），使用有向图表示变量间的依赖关系；
• 无向图模型或马尔可夫网（Markov network），使用无向图表示变量间相关关系。

监督学习的任务就是学习一个模型，对于给定的输入\(X\)，能预测出类别\(Y\)。所学习到的模型一般可表示为决策函数：

\begin{equation}
Y = f(X)
\label{eq:deci}
\end{equation}

或者为条件概率

\begin{equation}
\arg \mathop{max}\limits_{Y} P(Y|X)
\label{eq:cond}
\end{equation}

监督学习的模型分为生成模型（generative model）与判别模型（discriminative model）。生成模型学习联合概率分布\(P(X, Y)\)，然后通过贝叶斯定理求解条件概率\eqref{eq:cond}，而判别模型则是直接学习决策函数\eqref{eq:deci}或条件概率\eqref{eq:cond}。HMM属于生成模型的有向图PGM，通过联合概率建模：

\[
P(S,O) = \prod_{t=1}^{n}P(s_t|s_{t-1})P(o_t|s_t)
\]

其中，\(S\)、\(O\)分别表示状态序列与观测序列。HMM的解码问题为\(\arg \mathop{max}\limits_{S} P(S|O)\)；定义在时刻\(t\)状态为\(s\)的所有单个路径\(s_1^t\)中的概率最大值为

\[
\delta_t(s) = \max P(s_1^{t-1}, o_1^{t}, s_t=s)
\]

则有

\[
\begin{aligned}
\delta_{t+1}(s) & = \max P(s_1^{t}, o_1^{t+1}, s_{t+1}=s) \\
& = \max_{s'} P(s_1^{t-1}, o_1^{t}, s_t=s') P(s_{t+1}|s_t) P(o_{t+1}|s_{t+1}) \\
& = \max_{s'} [\delta_t(s') P(s|s')] P(o_{t+1}|s)
\end{aligned}
\]

上述式子即为（用于解决HMM的解码问题的）Viterbi算法的递推式；可以看出HMM是通过联合概率来求解标注问题的。

最大熵模型

最大熵（Maximum Entropy）模型属于log-linear model，在给定训练数据的条件下对模型进行极大似然估计或正则化极大似然估计：

\begin{equation}
P_w(y|x) = \frac{exp \left( \sum_i w_i f_i(x,y) \right)}{Z_w(x)}
\label{eq:me-model}
\end{equation}

其中，\(Z_w(x) = \sum_{y} exp \left( \sum_i w_i f_i(x,y) \right)\)为归一化因子，\(w\)为最大熵模型的参数，\(f_i(x,y)\)为特征函数（feature function）——描述\((x,y)\)的某一事实。

最大熵模型并没有假定feature相互独立，允许用户根据domain knowledge设计feature。

2. MEMM

MEMM并没有像HMM通过联合概率建模，而是直接学习条件概率

\begin{equation}
P(s_t|s_{t-1},o_t)
\label{eq:memm-cond}
\end{equation}

因此，有别于HMM，MEMM的当前状态依赖于前一状态与当前观测；HMM与MEMM的图模型如下（图来自于[3]）：

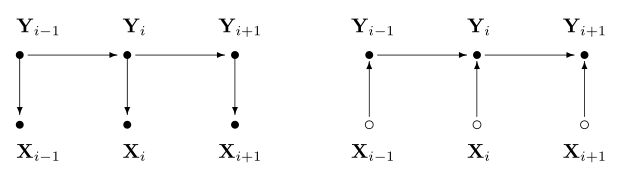
一般化条件概率\eqref{eq:memm-cond}为\(P(s|s',o)\)。MEMM用最大熵模型来学习条件概率\eqref{eq:memm-cond}，套用模型\eqref{eq:me-model}则有：

\begin{equation}
P(s|s',o) = \frac{ exp \left( \sum_a \lambda_a f_a(o,s) \right)}{ Z(o,s')}
\label{eq:memm-model}
\end{equation}

其中，\(\lambda_a\)为学习参数；\(a=<b,s>\)且\(b\)为feature，\(s\)为destination state；特征函数\(f_a(o,s)\)的示例如下（图出自于[6]）：

类似于HMM，MEMM的解码问题的递推式：

\[
\delta_{t+1}(s) = \max_{s'} \delta_t(s') P(s|s', o_{t+1})
\]

但是，MEMM存在着标注偏置问题（label bias problem）。比如，有如下的概率分布（图来自于[7])：

根据上述递推式，则概率最大路径如下：

但是，从全局的角度分析：

• 无论观测值，State 1 总是更倾向于转移到State 2；
• 无论观测值，State 2 总是更倾向于转移到State 2.

从式子\eqref{eq:memm-model}可以看出MEMM所做的是本地归一化，导致有更少转移的状态拥有的转移概率普遍偏高，概率最大路径更容易出现转移少的状态。因MEMM存在着标注偏置问题，故全局归一化的CRF被提了出来[3]。欲知CRF如何，请看下一篇分解。

3. 参考资料

[1] McCallum, Andrew, Dayne Freitag, and Fernando CN Pereira. "Maximum Entropy Markov Models for Information Extraction and Segmentation." Icml. Vol. 17. 2000.
[2] Xue, Nianwen, and Libin Shen. "Chinese word segmentation as LMR tagging." Proceedings of the second SIGHAN workshop on Chinese language processing-Volume 17. Association for Computational Linguistics, 2003.
[3] Lafferty, John, Andrew McCallum, and Fernando Pereira. "Conditional random fields: Probabilistic models for segmenting and labeling sequence data." Proceedings of the eighteenth international conference on machine learning, ICML. Vol. 1. 2001.
[4] 李航,《统计学习方法》.
[5] 周志华,《机器学习》.
[6] Nikos Karampatziakis, Maximum Entropy Markov Models.
[7] Ramesh Nallapati, Conditional Random Fields.