UVa 1393 (容斥原理、GCD) Highways

题意：

给出一个n行m列的点阵，求共有多少条非水平非竖直线至少经过其中两点。

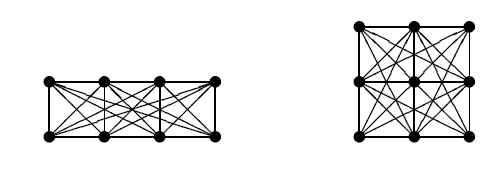
分析：

首先说紫书上的思路，编程较简单且容易理解。由于对称性，所以只统计“\”这种线型的，最后乘2即是答案。

枚举斜线包围盒的大小，如果盒子的长宽ab互质，则是可以的。这种盒子共有(m-a)(n-b)个，但要减去其中重复的。如果有一个长宽为2a和2b的大盒子，则计数右下角的小盒子的同时，左上角的小盒子会重复，所以要减去重复的盒子的个数c = max(0, m-2a) * max(0, n-2b)

最后gcd(a, b)的值是要预处理的

 #include <cstdio>
 #include <algorithm>

 const int maxn = ;
 int gcd[maxn+][maxn+];

 int GCD(int a, int b)
 {
     return b ==  ? a : GCD(b, a%b);
 }

 int main()
 {
     for(int i = ; i <= maxn; ++i)
         for(int j = ; j <= i; ++j)
             gcd[i][j] = gcd[j][i] = GCD(i, j);

     int n, m;
     while(scanf("%d%d", &n, &m) ==  && n)
     {
         int ans = ;
         for(int a = ; a <= n; ++a)
             for(int b = ; b <= m; ++b)
                 if(gcd[a][b] == )
                 {
                     int c = std::max(, n-a*) * std::max(, m-b*);
                     ans += (n-a)*(m-b) - c;
                 }

         printf("%d\n", ans * );
     }

     return ;
 }

代码君

解法二：

解法转自UVA 1393 - Highways (容斥原理计数)

dp(i, j)表示在长宽为ij的盒子中，从左上角最多能连多少条不重复的直线。

可以根据容斥原理递推dp(i, j) = dp(i-1, j) + dp(i, j-1) - dp(i-1, j-1) + (gcd(i, j) = 1) (因为盒子两边长互质的时候，才能连出一条新边出来)

最后答案ans递推的形式也是一样的，但重复的连线是那些缩小两倍后仍存在的直线

ans(i, j) = ans(i-1, j) + ans(i, j-1) - ans(i-1, j-1) + dp(i, j) - dp(i/2, j/2)

最后代码中，本想着只计算一半答案会快一点，结果排名21，登榜失败。

 #include <cstdio>
 #include <algorithm>

 const int maxn = ;
 int dp[maxn+][maxn+], ans[maxn+][maxn+];

 int gcd(int a, int b)
 {
     return b ==  ? a : gcd(b, a%b);
 }

 void Init()
 {
     for(int i = ; i <= maxn; ++i)
         for(int j = ; j <= i; ++j)
         {
             if(i == j) dp[i][j] = dp[i][j-] *  - dp[i-][j-] + (gcd(i, j) == );
             else dp[i][j] = dp[i-][j] + dp[i][j-] - dp[i-][j-] + (gcd(i, j) == );
         }

     for(int i = ; i <= maxn; ++i)
         for(int j = ; j <= i; ++j)
         {
             if(i == j) ans[i][j] = ans[i][j-] *  - ans[i-][j-] + dp[i][j] - dp[i/][j/];
             else ans[i][j] = ans[i][j-] + ans[i-][j] - ans[i-][j-] + dp[i][j] - dp[i/][j/];
         }
 }

 int main()
 {
     Init();
     int n, m;
     while(scanf("%d%d", &n, &m) ==  && n)
     {
         if(n < m) std::swap(n, m);
         printf("%d\n", ans[n-][m-]*);
     }

     return ;
 }

代码君