hiho拓扑排序专题 ——第四十八、四十七周

拓扑排序·一

分析：

此题就是求一个有向图中是否存在环。 如存在环则输出"Wrong"， 若不存在环， 说明课程安排的合理，输出"Correct"。

题中的提示说的已经十分清楚了。

总的来说就是：

① 找出入度为0的点（说明该点没有前驱），把该点放入集合T中。 把所有从该点出发的边都删除；

② 遍历剩余的点， 找出入度为0 的点， 重复①操作。

③直到不存在入度为0的点。 结束。如果此时集合T中包含所有的点， 那么该图不存在环， 否则存在环。

注意：1、执行操作①时， 在删除边时（u, v），同时更新与其相关点的入度（du[v]--）；

2、 在执行操作②时， 需要遍历所有点， 点少的时候可行， 点多的话很容易超时。 所以题目的提示中告诉了一个好办法就是： 执行操作①更新相关点的入度时直接判断一下是否为0， 若为零则入队列。 这样会省很多时间。

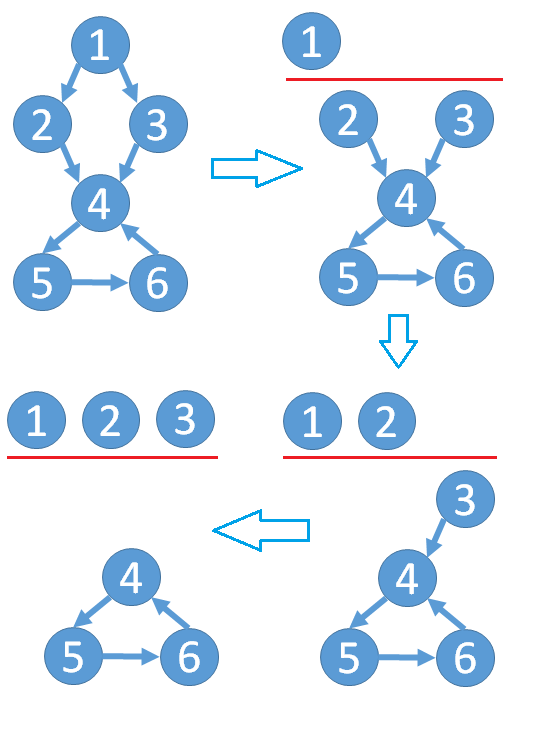
如下图例子：

开始点1入度为0， 点1加入集合T,   删除从1出发的边；  更新相关点的入度， 点2、3的入度都变为0了 ， 2、3入队列；

再依次对点2、3进行①操作， 2、3加入T,   删除边（2, 4）， （3， 4）， 此时没有其他点入度为0了， 结束操作， T中未包含所有点， 说明该图中有环；

#include<iostream>
#include<cstdio>
#include<cstring>
#include<string.h>
#include<algorithm>
#include<vector>
#include<queue>
using namespace std;

int t, n, m, sum, du[];
vector<int> vec[];

int ac()
{
    queue<int> q;
    for(int i = ; i <= n; i++)//遍历一边所有点， 把入度为0的点，全加入队列q中
    {
        if(du[i] == )
            q.push(i);
    }
    while(!q.empty())
    {
        int tem = q.front();//在队列中取出一个入度为0的点
        q.pop();
        sum++;
        //把所有从tem出发的边（tem， v）删除并更新du[],
        for(int i = ; i < vec[tem].size(); i++)
        {
            du[vec[tem][i]]--;
            if(du[vec[tem][i]] == )//若点vec[tem][i]入度更新后为0， 则入队列
                q.push(vec[tem][i]);
        }
        vec[tem].clear();
    }
    if(sum == n) return ;
    else
        return ;
}
int main()
{
    cin >> t;
    while(t--)
    {
        scanf("%d%d", &n, &m);
        //用vec[]来存边
        for(int i = ; i <= n; i++) vec[i].clear();
        memset(du, , sizeof(du));//初始化入度， 置为0；
        for(int i = ; i <= m; i++)
        {
            int x, y;
            scanf("%d%d", &x, &y);
            vec[x].push_back(y); // 加入边
            du[y]++; //记录入度
        }
        sum = ;
        int ans = ac();
        if(ans == )
            printf("Correct\n");
        else
            printf("Wrong\n");
    }
    return ;
}

拓扑排序·二

分析：

和上一道差不多， 只是多了一项就是记录每个点的病毒数。  每个点的病毒数 = 自身病毒数 +  所有能够达到它的节点病毒数之和（ 就是所有它前驱点的病毒数的和）。

#include<iostream>
#include<cstdio>
#include<cstring>
#include<string.h>
#include<algorithm>
#include<vector>
#include<queue>
using namespace std;
const int mod = ;
int n, m, k, sum, virus[], du[];
vector<int> vec[];

void ac()
{
    queue<int> q;
    for(int i = ; i <= n; i++)
    {
        if(du[i] == )
            q.push(i);
    }
    while(!q.empty())
    {
        int tmp = q.front(); q.pop();
        sum = (sum + virus[tmp]) % mod;  

        //把所有前驱点为 tmp 的点的病毒数都加上 tmp的病毒数
        for(int i = ; i < vec[tmp].size(); i++)
        {
            int b = vec[tmp][i];
            virus[b] = (virus[tmp] + virus[b]) % mod;// 此处也一定要取模，
            du[b]--;
            if(du[b] == )
                q.push(b);
        }
        vec[tmp].clear();
    }
}
int main()
{
    while(scanf("%d%d%d", &n, &m, &k) != EOF)
    {
        memset(virus, , sizeof(virus));
        memset(du, , sizeof(du));
        for(int i = ; i <= n; i++) vec[i].clear();

        for(int i = ; i <= k; i++)
        {
            int x;
            scanf("%d", &x);
            virus[x]++;
        }
        for(int i = ; i <= m; i++)
        {
            int x, y;
            scanf("%d%d", &x, &y);
            vec[x].push_back(y);
            du[y]++;
        }

        sum = ;
        ac();
        printf("%d\n", sum);
    }
    return ;
}