bzoj千题计划279：bzoj4591: [Shoi2015]超能粒子炮·改

http://www.lydsy.com/JudgeOnline/problem.php?id=4591

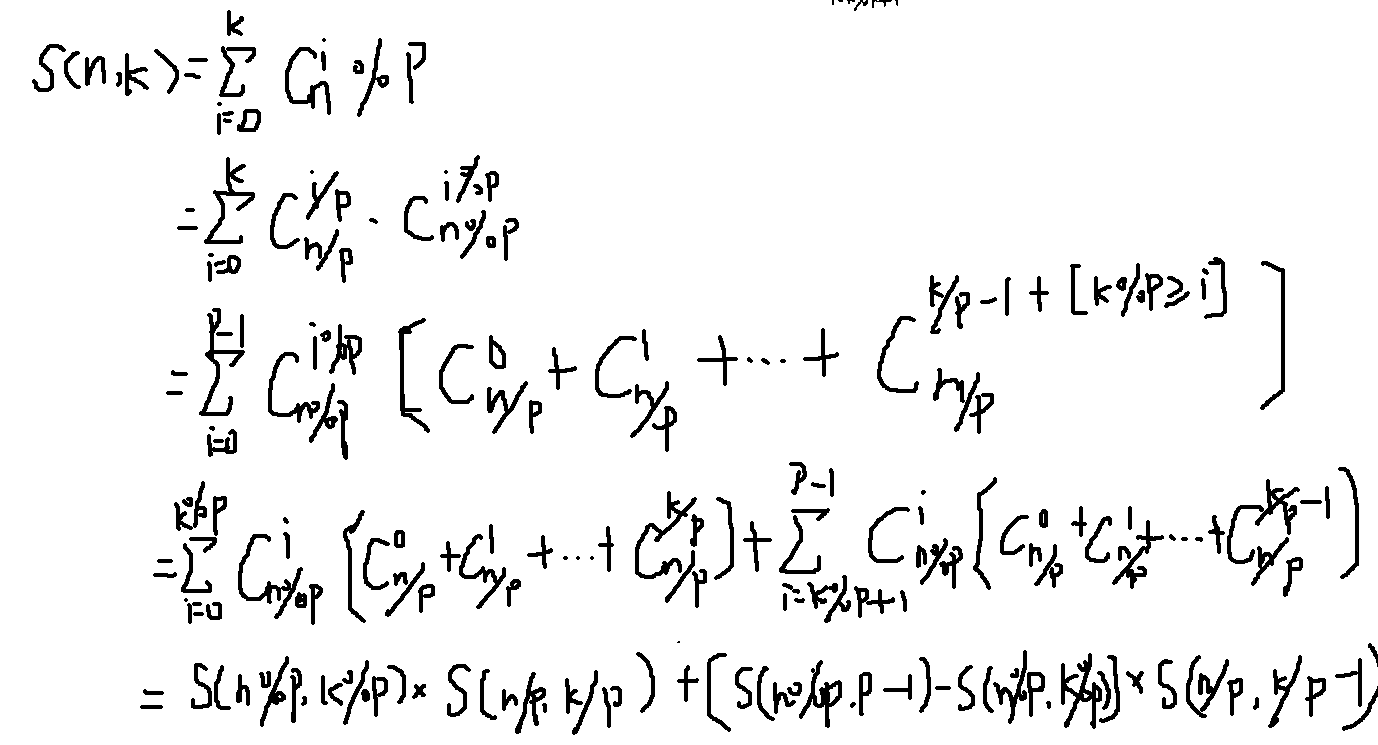
最后的式子合并同类项

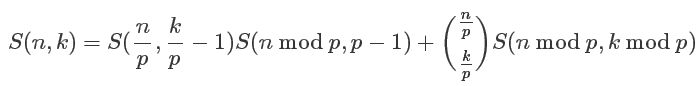
#include<cstdio>
#include<iostream>

using namespace std;

typedef long long LL;

const int p=;

int C[][],s[][];

template<typename T>
void read(T &x)
{
    x=; char c=getchar();
    while(!isdigit(c)) c=getchar();
    while(isdigit(c)) { x=x*+c-''; c=getchar(); }
}

void pre()
{
    C[][]=;
    for(int i=;i<=p;++i)
    {
        C[i][]=;
        for(int j=;j<=i;++j) C[i][j]=(C[i-][j-]+C[i-][j])%p;
    }
    for(int i=;i<=p;++i)
    {
        s[i][]=C[i][];
        for(int j=;j<=p;++j) s[i][j]=(s[i][j-]+C[i][j])%p;
    }
}

int Lucas(LL n,LL m)
{
    if(n<m) return ;
    int ans=;
    for(;m;n/=p,m/=p) ans=ans*C[n%p][m%p]%p;
    return ans;
}

int S(LL n,LL k)
{
    if(k<) return ;
    if(n<=p && k<=p) return s[n][k];
    return (S(n%p,k%p)*Lucas(n/p,k/p)+S(n%p,p-)*S(n/p,k/p-))%p;
}

int main()
{
    int T;
    LL n,k;
    pre();
    read(T);
    while(T--)
    {
        read(n); read(k);
        printf("%d\n",S(n,k));
    }
}