沉迷AC自动机无法自拔之：[UVA 11468] Substring

图片加载可能有点慢，请跳过题面先看题解，谢谢

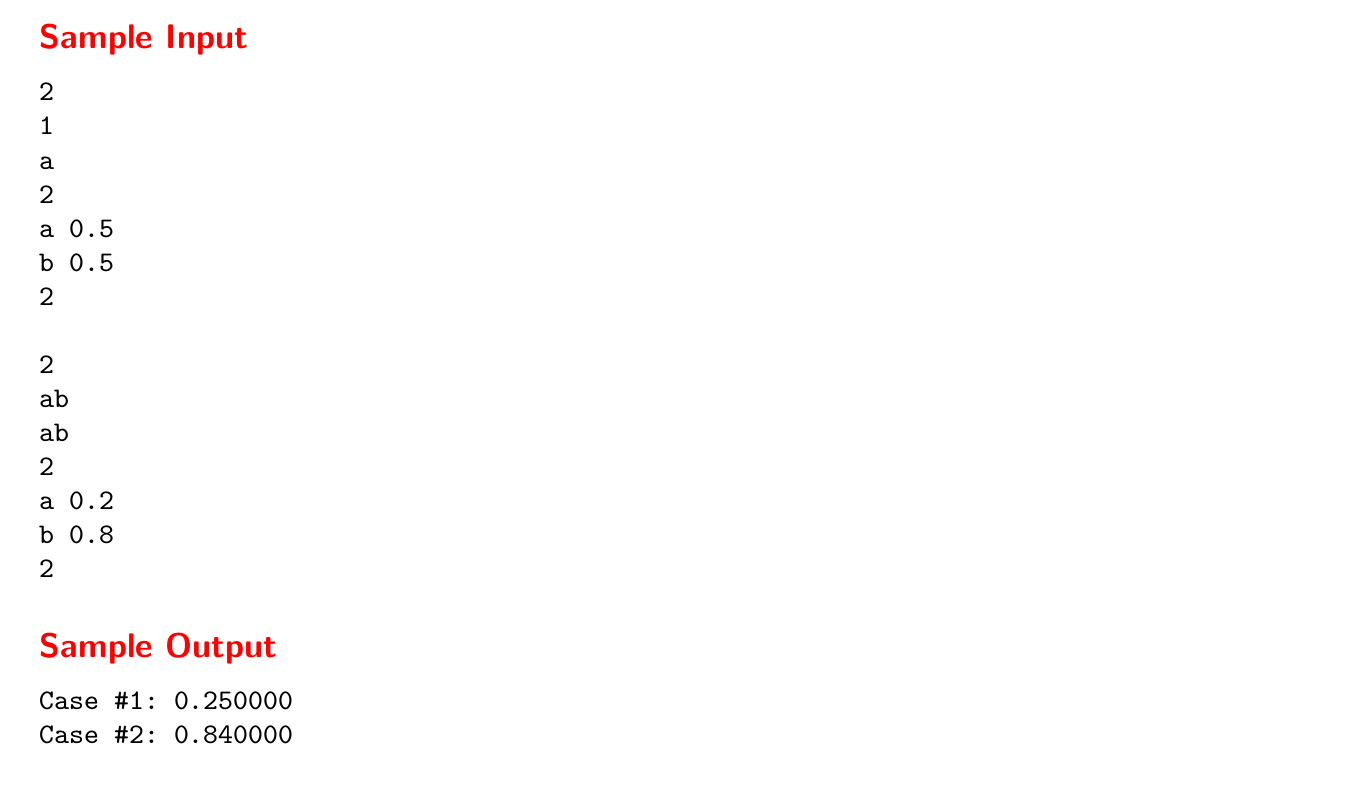
这个鬼题目，上一波套路好了
先用题目给的模板串建\(AC\)自动机，把单词结尾标记为 \(val=1\)，然后在建好的\(AC\)自动机上跑 \(dp\)，
设 \(f[x][L]\) 为：当前在 \(x\) 节点，剩下还要走 \(L\) 步并且不经过单词结尾的概率
那么有转移： \(f[x][L]=\sum_{!val[son[x][i]]}p[i]*dp(son[x][i],L-1)\)，可以记忆搜实现
$
$

//made by Hero_of_someone
#include<iostream>
#include<cstdio>
#include<cstdlib>
#include<cstring>
#define db double
#define il inline
using namespace std;

int T,t,n,m,L,id[150];
char s[25][25];
db p[65];

struct Tire{
   int son[540][65],fail[540],size,root,val[540];
   bool vis[540][110]; db f[510][110];
   il void init(){
      size=1; root=0;
      memset(son,0,sizeof(son));
      memset(val,0,sizeof(val));
      memset(vis,0,sizeof(vis));
      memset(fail,0,sizeof(fail));
   }

   il void insert(char *s){
      int cur=root;
      for(int i=0;s[i];i++){
         int idx=id[s[i]];
         if(!son[cur][idx]) son[cur][idx]=size++;
         cur=son[cur][idx];
      }
      val[cur]=1; return ;
   }

   il void build(){
      int que[1010],hd=0,tl=0;
      for(int i=0;i<n;i++)
         if(son[root][i]){
            que[tl++]=son[root][i];
            fail[son[root][i]]=root;
         }
         else son[root][i]=root;
      while(hd<tl){
         int cur=que[hd++];
         for(int i=0;i<n;i++){
            int Son=son[cur][i];
            if(Son){
               int f=fail[cur];
               while(f && !son[f][i]) f=fail[f];
               fail[Son]=son[f][i];
               val[Son]|=val[fail[Son]];
               que[tl++]=Son;
            }
            else son[cur][i]=son[fail[cur]][i];
         }
      }
   }

   il db dfs(int x,int L){
      if(!L) return 1.0;
      if(vis[x][L]) return f[x][L];
      vis[x][L]=1;
      db ret=0.0;
      for(int i=0;i<n;i++){
         if(val[son[x][i]]) continue;
         ret+=p[i]*dfs(son[x][i],L-1);
      }
      return f[x][L]=ret;
   }
}AC;

il void init(){
   AC.init();
   scanf("%d",&m); for(int i=1;i<=m;i++) scanf("%s",s[i]);
   scanf("%d",&n);
   for(int i=0;i<n;i++){
      char ss[10];
      scanf("%s %lf",ss,&p[i]);
      id[ss[0]]=i;
   }
   for(int i=1;i<=m;i++) AC.insert(s[i]);
}

il void work(){ AC.build(); scanf("%d",&L); printf("Case #%d: %.6lf\n",t,AC.dfs(0,L)); }

int main(){ scanf("%d",&T); for(t=1;t<=T;t++){ init(); work(); } return 0; }