Algorithms学习笔记-Chapter0序言

0.开篇

《Algorithms》源自Berkeley和UCSD课程讲义，由   Sanjoy Dasgupta / Christos H. Papadimitriou / Umesh Vazirani 编写。

豆瓣链接：https://book.douban.com/subject/1996256/

中文版：https://book.douban.com/subject/3155710/

1.Algorithm

伴随数字系统的发展，算法“Algorithm”作为计算方法逐渐发展壮大，推动了社会发展。

设计算法需要注意的三个问题：

• 算法是否正确
• 算法性能怎样/复杂度多少？
• 还能怎样改进？

2.Fibonacci

定义：

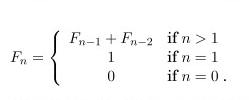
可知F_n  = 2^0.694n，指数级。

• 递归定义算法fib1

正确性肯定能保证，复杂度为指数级

• 多项式算法fib2

算法复杂度为O(n)

3.O符号

前面的分析中，将一个语句抽象为一次操作，然而fib数极大的时候，两大数相乘所需时间比小整数相乘时间多很多，即“Arithmetic operations on arbitrarily large numbers cannot possibly be performed in a single, constant-time step”，所以前面的抽象并不完全合理。

随着整数增大，n位整数相乘复杂度为O(n)(见Chapter 1)，因此fib2复杂度应为O(n²)。

O符号表示复杂度在常数范围内的上界。

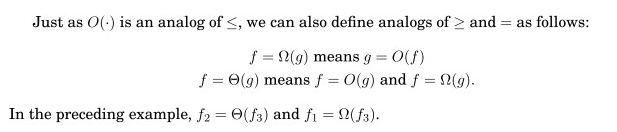
Ω表示常数范围内的下界，而a = θ(b)表示a处于常数倍b的范围内。

4.Exercise 0.4

是否存在比fib2更快的Fibonacci算法？

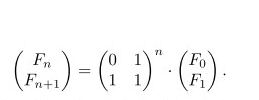
利用矩阵乘积，仅需求中间矩阵的n次方。

普通的算法需要n次连乘。从矩阵的角度来考虑，该矩阵满秩，因此矩阵Mⁿ可以分解成Q^TVⁿQ，其中Q为特征向量列组成的矩阵，V为特征值对角阵。这样只需要对求特征值的n次幂即可。