散列(Hash)表入门

一、概述

以 Key-Value 的形式进行数据存取的映射(map)结构

简单理解：用最基本的向量(数组)作为底层物理存储结构，通过适当的散列函数在词条的关键码与向量单元的秩(下标)之间建立映射关系

更详细的定义：开辟物理地址连续的桶数组ht[]，借助散列函数hash()，将词条关键码key映射为桶地址(数组下标)，从而快速地确定待操作词条的物理位置。

1.1 散列结构优点

• 可以实现O(1)时间的数据项查找（注：给定关键码，通过散列函数可直接计算出所在地址）
• 能以节省空间的方式实现上述O(1)查找

1.2 部分概念

1. 桶/桶单元（bucket）：散列表的物理存储结构，在物理上连续排列的用于存放词条的单元。
2. 桶数组（bucket array）：用数组作为桶单元。
3. 地址空间（address space）：桶数组的合法秩区间，如容量为R 则地址空间为[0, R)。
4. 散列函数（hash function）：词条与桶地址之间的映射关系，即从关键码到桶数组地址空间的映射函数。
5. 散列地址（hashing address）：给定关键码所对应的桶的秩，即 若给定散列函数hash()，关键码key，则散列地址为hash(key)。
6. 散列冲突（collision）：关键码不同的词条被映射到统一散列地址的情况。
7. 装填因子（load factor）：散列表中非空桶数量与桶单元总数的比值。
8. 完美散列（perfect hashing）：时间与空间性能均最优的散列。即给定问题实例下，对于任意关键码，均可在O(1)时间查找确定，且每个桶恰好存放一个词条，无空余无重复。完美散列实际上并不常见。
9. 词条的聚集（clustering）：词条集中到散列表内少数若干桶中（或附近）的现象。

1.3 简单的散列表设计实例

需求

存储某校2500门固定电话号码及其相关信息，号码随机分布在 0000-0000~9999-9999之间，需在O(1)时间进行高效查找。

简单设计

直接使用[99999999]的数组，以电话号码直接作为秩，即 hash(key)=key

缺点

这样设计缺点很明显：在词典中需要保存的词条数远小于关键码所有可能的情况下，直接用hash(key)=key 作为秩，导致装填因子太小，即实际装填数远小于桶单元总数，从而造成大量空间的浪费。

因此，需要合理设计散列函数，能够只创建实际需要保存数量的桶，并将关键码空间压缩到散列地址空间

二、散列函数

2.1 设计原则

散列函数首先面对的问题就是 散列冲突(Collision)，该问题必然存在，需尽可能避免，后续会提到相关解决方法。

其次便是以下一些设计原则：

1. 确定性，不论所含数据项如何，词条E的散列地址hash(E.key)必须完全取决于E.key。
2. 映射过程自身不能过于复杂，保证散列地址计算可快速完成
3. 所有关键码经映射后应尽量覆盖整个桶地址空间，以充分利用，即尽量满射。
4. （重要）关键码映射到各桶的概率应尽量接近于1/M，M为桶总数（若关键码本身均匀且独立随机分布，则这也是任意一对关键码相互冲突的概率）

总之随机性越强、规律性越弱的散列函数越好。（使得在M上分配均匀，降低冲突）

2.2 常见散列方法

1) 除余法（division method）

思路

最简单的散列办法，将散列表(桶)长度M取作素数，然后用关键码key与M取余作为散列地址。

取余使得散列地址分配概率既均匀，也不会>=M，正好符合散列地址空间

表达式

hash(key) = key % M

为什么M需要为素数？

实际应用中，存储的词条关键码往往具有某种周期性，如{1000,1015,1030...}，若周期与M若具有公共素因子，则冲突概率急剧攀升。

一般地，若M与词条关键码间隔T(上例为5)之间的最大公约数越大，则发生冲突可能性也越大。【TODO：底层数学原理暂无法探究】

注：若关键码本身独立随机，则概率还是平均的，只是在周期存取的情况下才会出现该情况。

2) MAD法（multiply-add-divide method）

除余法存在的不足

除余法虽能一定程度保证词条均匀分布，但从关键码空间到散列地址空间依然残留有一定的连续性，如 相邻关键码对应散列地址也相邻。

因此便有mad法，若常数ab选取得当，可以很好地克服除余法的这种连续性。除余法也可以看作Mad法a=1和b=0的特例，只是两个常数并未发挥实质作用。

表达式

hash(key) = (a*key+b) % M， 其中M仍为素数,a>0,b>0，且a % M != 0

3) 数字分析法（selecting digits）

注：以下各方法为保证落在合法的散列地址空间上，最后通常还需对表长M取余。

思路

从关键码key特定进制的展开中抽取特定的若干位，构成整型地址。

表达式

例：选取key十进制展开中的奇数位

hash(123456789) = 13579

4) 平方取中法（mid-square）

思路

从关键码key的平方的十进制或二进制展开中取居中的若干位，构成一个整型地址。

表达式

例：取平方并用十进制展开中的居中3位作为散列地址

123^2 = 15129，hash(123) = 512

5) 折叠法（folding）

思路

将关键码的十进制或二进制展开分割成等宽的若干段，取其总和作为散列地址。

表达式

例：以十进制三个数位为分割单位

hash(123456789) = 123+456+789 = 1368

6) 异或法（xor）

思路

将关键码的二进制展开分割成等宽的若干段，经异或运算得到散列地址。

表达式

例：以二进制三个数位为分割单位

hash(411) = hash(110011011b) = 110^011^011 = 110b = 6

三、冲突及排解策略

3.1 冲突的普遍性

冲突必然的

因为用短位(散列地址空间)表示长位数据(关键码空间)，肯定会出现冲突。比如 常见的 MD5 码，一共就128bit，但却要表示无限的数据的散列码，因此必然会出现不同数据具有相同MD5码的情况。

3.2 冲突排解策略

冲突排解策略分为以下两种类型：

• 开放定址(open addressing) / 闭散列(closed hashing)：散列地址空间对所有词条开放（即 桶单元允许装hash(key)不对应的词条）；词条存储地址(散列地址)仅限于散列表所覆盖的范围之内。
  
  如：线性试探、查找链法等。
  
  注：因闭散列不得使用附加空间的原因，装填因子通常<=0.5
• 封闭定址(closed addressing) / 开散列(open hashing)：散列地址空间只对对应的词条开放；词条存储地址不局限于散列表范围之内。
  
  如：多槽位法、独立链法、公共溢出区等

1）多槽位法（multiple slots）

思路

每个桶本身再细分为若干槽位，用于存放彼此冲突的词条。每个桶槽位的词典结构为向量，因此整体物理存储结构类似于二维数组。

如：put操作，首先通过hash(key)定位到对应的桶单元，并在该桶内部槽位中进一步查找key，若没找到，则创建新词条插入到该桶的空闲槽位中。

缺点

1. 绝大多数的槽位都处于空闲状态，造成空间浪费。若桶被细分为k个槽位，则装填因子将直接降低为原来的1/k.
2. 很难实现确定应该细分为多少个槽位，才能保证够用。

2) 独立链法(separate chaining) / 拉链法

思路

与多槽位思想类似，但每个桶的子词典是使用链表实现，令彼此冲突的词条互相串接。

优点

能灵活动态地调整子词典的规模，有效地使用空间。

缺点

空间未必连续分布，会导致系统缓存失效。

3) 公共溢出区

原理

在原散列表之外另设一个词典结构$$D_{overflow}$$，插入词条一旦发生冲突，则转存到该词典中。$$D_{overflow}$$相当于存放冲突词条的公共缓冲池。

4) 线性试探法

原理

在插入词条时，若发生冲突，则转而试探桶单元ht[hash(key)+1]，若ht[hash(key)+1]也被占用，则继续试探ht[hash(key)+2]，如此不断...直到找到空桶。

第i次试探的散列地址：(hash(key) + i) mod M, i=1,2,3...

具体查找逻辑

查找链(probing chain)：对于待查找的key，从hash(key)桶单元开始，直接空桶结束的顺序序列。

1. 经hash(key)算得的当前桶单元，若关键码相等，则成功返回。
2. 当前桶单元非空，但关键码不等，则转入下一桶单元继续试探。
3. 当前桶为空，则返回查找失败。

注：相互冲突的关键码比属于同一查找链（即中途不包含空桶），但同一查找链的关键码未必相互冲突。多组各自冲突的关键码所对应的查找链，有可能相互交织和重叠。

优点

具体由良好的数据局部性，试探地桶单元在物理空间上依次连贯，系统缓存能发挥作用。

懒惰删除

定义：

从词典删除词条时，暂时并不实际将桶置空，而是额外维护一个删除标记Bitmap，标记该桶已删除。

为什么需要懒惰删除？

因为查找链中任何一环的缺失，都会导致后续词条的“丢失”，即无法找到已存在词条；同时因为开销问题，不可能每次删除操作都对查找链进行维护重建（在扩容时，才重建链）。

因此懒惰删除机制既能保证查找链的完整，也不需要太多开销。

加入懒惰删除后，操作逻辑的变化：

1. 在删除等操作查询指定词条时，判断失败的条件变为：为空且不带懒惰删除标记。
2. 在插入操作时，找空桶过程中，判断桶为空条件为：带有懒惰标记或当前桶为空。

5) 平方试探法

线性试探法的不足

线性试探法各查找链均由物理上连续的桶单元组成，会加剧关键码的聚集趋势。

定义

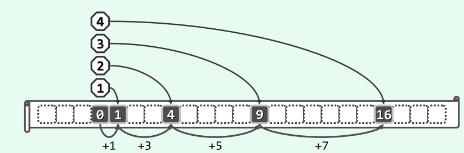
若发生冲突，则第j次试探地桶地址：(hash(key) + j^2) mod M, j=0,1,2...

该方式会使得试探地址加速逃离聚集区段。

该方式局部性会有所降低，但如今I/O页面规模较大，不必过于担心。

确保试探必然终止

只要散列表长度M为素数，且装填因子$$\lambda<=50%$$，则平方试探必然会终止于某个空桶。（数学证明暂未探究）

6) 再散列法（double hashing）

选取一个适宜的二级散列函数$$hash_2()$$，一旦发生冲突，则将再散列的结果作为偏移量，公式如下：

第 j 次试探地址：$$[hash(key)+j*hash_2(key)]%M$$

四、散列码转换 hahsCode()

4.1 定义

散列码(hash code)：利用某一种散列码转换函数hashCode()，将关键码key统一转换为的一个整数。

4.2 为什么需要散列码

因为词条关键码不一定天然支持大小比较，而且也并不一定是整数类型，因此需制定一个函数能将任意类型的关键码先统一转成散列码，散列函数再由散列码计算散列地址。

4.3 散列码转换函数设计原则

1. 作为中间桥梁的散列码，取值范围应覆盖系统所支持的最大整数范围
2. 各关键码经hashCode()映射后的散列码之间，也应尽可能减少冲突。否则在该阶段的冲突，后续hash()必定无法消除。
3. hashCode()应与判等器保持一致。即 判等器判断相等的对象，其散列码应该相等。

参考：

数据结构 邓俊辉