001.Parted工具使用

一 Parted简介

1.1 parted和fdisk

通常使用较多的磁盘管理工具为fdisk，但由于磁盘越来越廉价，且磁盘空间越来越大，而fdisk工具分区存在大小限制，只能划分小于2T的磁盘。因此需要使用Parted工具来实现对GPT磁盘进行分区操作，parted工具同样具有两种模式：命令行模式和交互模式。

GPT格式的磁盘相当于原来MBR磁盘中原来保留4个partition table的4*16个字节，只留第一个16个字节，类似于扩展分区，真正的partitiontable在512字节之后，GPT磁盘没有四个主分区的限制。

1.2 交互模式常用参数

命令	含义
help	获取帮助信息。
mklabel	创建分区表，设置使用msdos还是gpt格式。
mkpart	创建新分区，命令格式：mkpart PART-TYPE [FS-TYPE] START END PART-TYPE：表示分区类型，如primary（主分区）、extended（扩展分区）、logical（逻辑分区）； FS-TYPE：表示文件系统类型，如fat32、ntfs、ext2、ext3、ext4等； START：表示分区的起始位置； ENS：表示分区的结束位置。
print	输出分区信息，可简写为p，相关选项如下： free：显示该磁盘的所有信息，并显示剩余空间； number：显示指定分区的信息； all或list：显示所有磁盘信息。
rm	删除分区，命令格式rm number。
select	选择设备，进入parted交互模式后，系统默认选择的是第一块硬盘。 可使用select [磁盘设备]切换至需要操作的硬盘。

二 Parted实例

2.1 Parted安装

 [root@study ~]# yum -y install parted

2.2 增删改操作

 [root@study ~]# parted -l			#也可结合fdisk命令确认需要操作的磁盘设备名

 [root@study ~]# parted
 (parted) select /dev/sda			#选择sda设备
 (parted) p 					#显示当前磁盘设备信息
 ……
 Partition Table: msdos				#磁盘分区类型为msdos
 (parted) select /dev/sdb			#选择sdb磁盘进行操作

 

 (parted) mklabel gpt					#将磁盘分区表类型设置为gpt格式

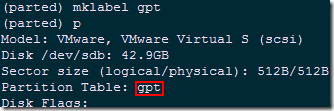
 (parted) mkpart primary 0gb 10gb			#创建primary分区，从0gb起始，10gb结束

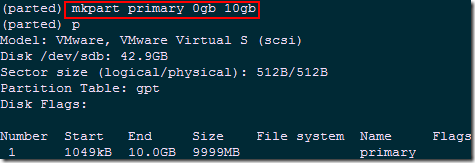
 (parted) mkpart primary 10gb 15gb 			#继续创建第二个5g大小的分区

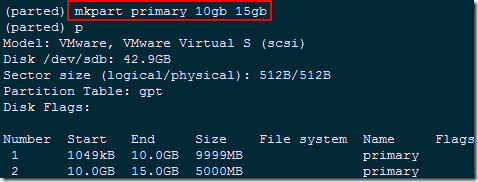
 (parted) p free					#查看当前sdb的空闲磁盘空间

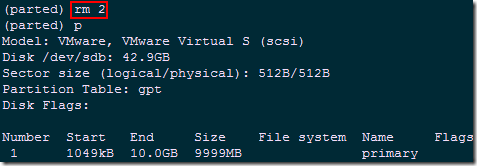
 (parted) rm 2					#删除2号分区

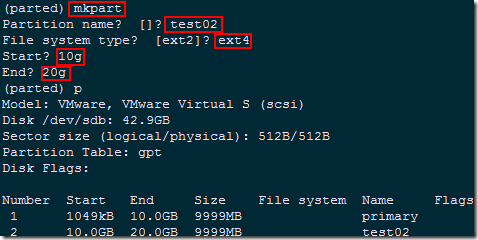
 (parted) mkpart
 Partition name?  []? test02
 File system type?  [ext2]? ext4
 Start? 10g
 End? 20g
 #使用mkpart交互逐步创建分区

 

(parted) q

三 格式化并挂载

略