AC自动机学习笔记-1（怎么造一台AC自动机?）

月更博主又来送温暖啦QwQ

今天我们学习的算法是AC自动机。AC自动机是解决字符串多模匹配问题的利器，而且代码也十分好打=w=

在这一篇博客里，我将讲解AC自动机是什么，以及怎么构建一个最朴素的AC自动机。（不知道为什么我写出来的AC自动机常数就是大得要命=。=）

前置知识

首先你一定要对Trie树以及KMP了如指掌，尤其是要明白KMP中失配数组(next或fail数组)的本质:利用已经匹配过的部分，跳过重复的匹配，达到快速匹配的目的。

AC自动机是什么

大家都知道KMP可以用于在一个大字符串（文本串）中寻找另一个小的字符串（模式串），那么如果有n个模式串，要你把它们全部在文本串中找出来呢？当然，我们可以做n次KMP（别小瞧30分哦），但是其效率并不能差强人意。这个时候，我们可以尝试把模式串做成Trie树，似乎可以提高效率。

比如说，我们有5个模式串：she,shr,say,he,her,那么它们所建出来的Trie树应该是长成这样的：（红色节点表示单词的结尾）

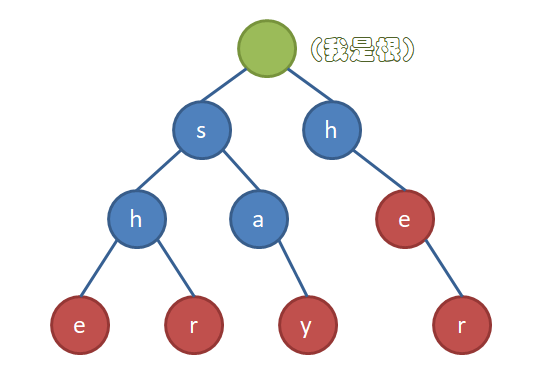
那么，怎么用它来匹配呢？如果我们把文本串的每一个点都作为起点放到Tire树上匹配，它的复杂度将会是...我要你Tire树有何用(╯‵□′)╯︵┻━┻

既然这样，那么如果只把文本串的第一个字符为起点，会发生什么呢？

你以为会是这样的：

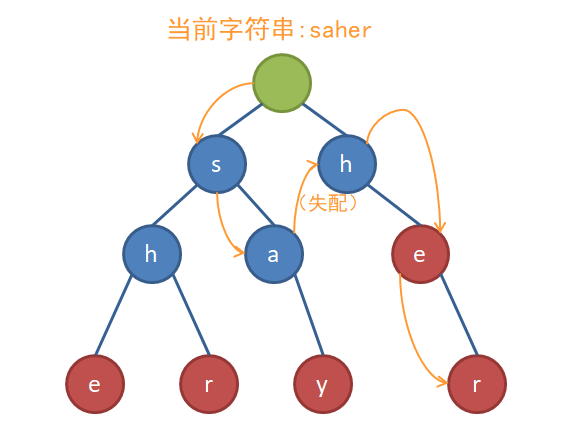
完美！

然而实际上却是这样的：

问题很明显，当我们匹配完she时，he其实也被匹配到了。所以我们希望这棵Trie树上能够加点东西，让它可以达到下面的效果：

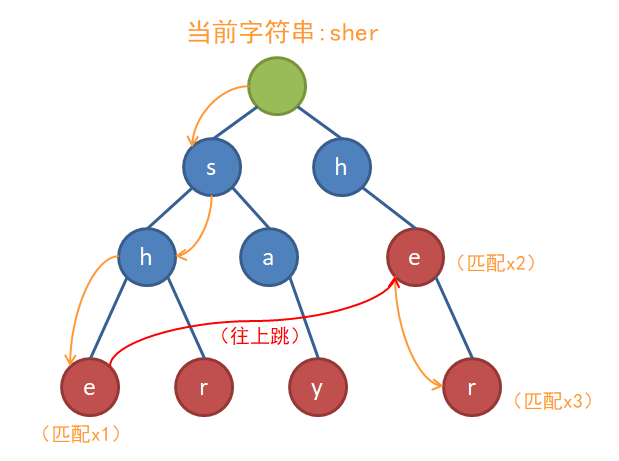
上图中，红色的箭头就是失配指针——fail指针。它表示文本串在当前节点失配后，我们应该到哪个节点去继续匹配。很显然，对于每个节点，我们要找到这个节点-代表的字符串-在树上所有的节点-表示的字符串中-能找到的最长的后缀，意思就是“我当前匹配到了这个点，我也相当于匹配到了的节点（中的深度最大的节点）。”比如说，在我举的例子中，当我们匹配到了she时，我们在树上走的路径也包含了he，he是she的一个后缀。我们在she上失配，至少说明我们已经匹配到了he，于是就可以跳到代表he的节点上继续匹配。

到这里，你是不是发现fail指针和KMP中的next指针简直一毛一样？它们都被称为“失配指针”。将Trie树上的每一个点都加上fail指针，它就变成了AC自动机。AC自动机其实就是Trie+KMP，它可以用来解决在文本串中寻找很多模式串，即多模匹配问题。

对于一开始的5个单词，它们所构建出的AC自动机就长这样（没有画出红色箭头的点，其fail指针都指向根节点）：

如何构建AC自动机

显然，我们要做的就是快速地求出所有点的fail指针。我们以bfs的顺序依次求出每个节点的fail，这样，当我们要求一个节点的fail时，它的父亲的fail肯定已经求出来了。若当前节点为A，其父节点为B，B的fail为C，那么C所代表的字符串一定是B的最长的后缀。如果C有一个儿子D的字符与A的字符等同，那么显然D所代表的串（C加一个字符）就是A所代表的串（B加一个字符）的最长后缀。如果C没有一个儿子，使其字符与A的字符等同呢？很简单，只需要再访问C的fail就行了。如此反复，直到A的最长后缀找到，或者A的fail指向根节点为止。（A在Trie树中没有后缀，乖乖回到根重新匹配吧！）

为了解释得更清楚，我举一个例子。下面这幅图是我根据别的地方的图重新画的（n次转载？），出处我没找到_(:з」∠)_。节点是根据bfs序标号的。

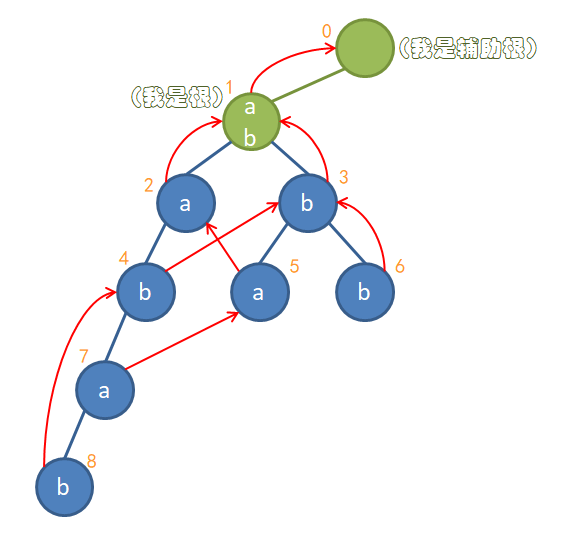
步骤：

1. 为了少一些特判，设置一个辅助根节点0号节点，0号节点的所有儿子都指向真正的根节点1号节点，然后将1号节点的fail指向0号节点。
2. 找到2号节点的父亲节点的fail节点0号节点，看0号节点有没有为a的子节点。有，于是2号节点的fail指向1号节点。
3. 找到3号节点的父亲节点的fail节点0号节点，看0号节点有没有为b的子节点。有，于是3号节点的fail指向1号节点。
4. 找到4号节点的父亲节点的fail节点1号节点，看1号节点有没有为b的子节点。有，于是4号节点的fail指向3号节点。
5. 同上。
6. 同上。
7. 同上。
8. 找到8号节点的父亲节点的fail节点5号节点，看5号节点有没有为b的子节点。没有，于是再找到5号节点的fail节点2号节点，看2号节点有没有为b的子节点。有，于是8号节点的fail指向4号节点。

这样，一个AC自动机就做好了。

注意到由于辅助节点的存在，我们不需要做任何特判，在树上没有后缀的节点的fail指针会自动连向根节点。

构建fail指针的代码：

void build()
{
	for(int i=0;i<26;++i)ch[0][i]=1;
    fail[1]=0;
    queue<int>q;
    q.push(1);
    while(!q.empty())
    {
    	int x=q.front();q.pop();
        for(int i=0;i<26;++i)
        {
        	int c=ch[x][i];
            if(!c)continue;
            int fa=fail[x];
            while(fa&&!ch[fa][i])fa=fail[fa];
            fail[c]=ch[fa][i];
            q.push(c);
        }
    }
}

如何利用AC自动机来查找

这个问题似乎显而易见，只要根据文本串的内容沿着Trie树的边往下走就行了，一失配就沿着fail边向上跳。

。。。

我在被大佬虐飞之前也是这么想的QwQ

fail边不只是失配指针这么简单，如果你像我刚才说的那么做的话，你就可能会面临下面这样的问题：

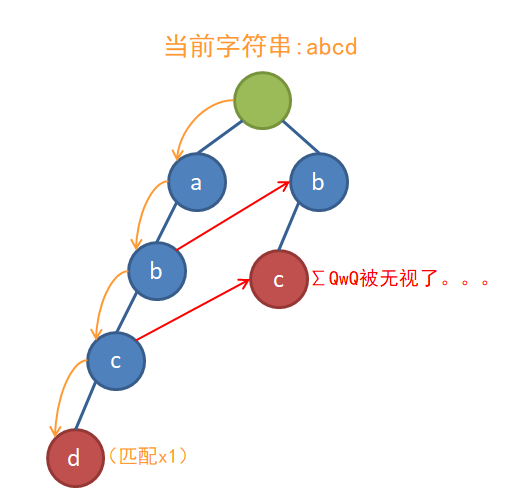
为了不让这种事情发生，我们每遇到一个fail指针就必须向上跳到顶，以保证不会漏过任何一个子串，就像这样：

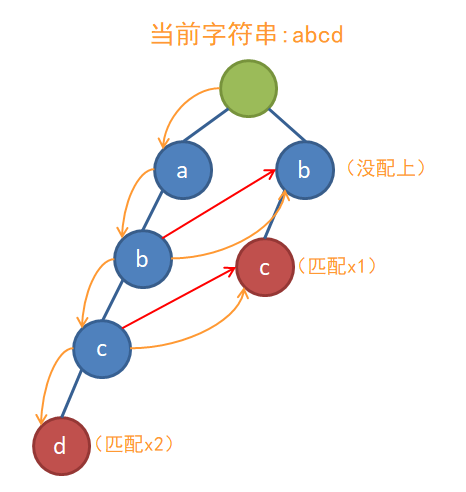
当然，这样未免也太蠢了，于是这里又有一个小优化：如果一个节点的fail指向一个结尾节点，那么这个点也成为一个（伪）结尾节点。在匹配时，如果遇到结尾节点，就进行相应的计数处理。

进行匹配的代码：

void print(int x)
{
	while(x)
    {
    	if(end[x])
        {
			//计数、打印等等，视题目要求而定
        }
        x=fail[x];
    }
}

void match(char *s)
{
	int len=strlen(s),now=1;
    for(int i=0;i<len;++i)
    {
    	int id=s[i]-'a';
        while(now&&!ch[now][id])now=fail[now];
        now=ch[now][id];
        if(end[now]||en[now])print(now);
        //en[now]即为伪结尾标记
    }
}

//记得在build中加上这句话
void build()
{
	...
    if(end[fail[c]]||en[fail[c]])en[c]=1;
    ...
}

一个被我们忽略的问题

时间复杂度？？？

设模式串平均长度为 $ l $ ，建树复杂度为 $ O(nl) $ ，构建fail指针为 $ O(nl) $ ，匹配时因为每次都要跳fail边，复杂度上界可以达到 $ O(ml) $ ，所以总复杂度为 $ O((n+m)l) $ ！

这和暴力有什么区别(╯°Д°)╯︵┻━┻？？？

虽然说，这个上界应该是十分松的，但是我们想要的是能跑 $ 1e6 $ 的速度！

这个时候我们就需要优化了。。。然而我已经没时间写辣QwQ!这些就留到下一篇博客吧！

谢谢你的资瓷啦QwQ!