Android中图像变换Matrix的原理、代码验证和应用（一）

第一部分 Matrix的数学原理

在Android中，如果你用Matrix进行过图像处理，那么一定知道Matrix这个类。Android中的Matrix是一个3 x 3的矩阵，其内容如下：

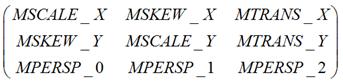
Matrix的对图像的处理可分为四类基本变换：

Translate           平移变换

Rotate                旋转变换

Scale                  缩放变换

Skew                  错切变换

从字面上理解，矩阵中的MSCALE用于处理缩放变换，MSKEW用于处理错切变换，MTRANS用于处理平移变换，MPERSP用于处理透视变换。实际中当然不能完全按照字面上的说法去理解Matrix。同时，在Android的文档中，未见到用Matrix进行透视变换的相关说明，所以本文也不讨论这方面的问题。

针对每种变换，Android提供了pre、set和post三种操作方式。其中

set用于设置Matrix中的值。

pre是先乘，因为矩阵的乘法不满足交换律，因此先乘、后乘必须要严格区分。先乘相当于矩阵运算中的右乘。

post是后乘，因为矩阵的乘法不满足交换律，因此先乘、后乘必须要严格区分。后乘相当于矩阵运算中的左乘。

除平移变换(Translate)外，旋转变换(Rotate)、缩放变换(Scale)和错切变换(Skew)都可以围绕一个中心点来进行，如果不指定，在默认情况下是围绕(0, 0)来进行相应的变换的。

下面我们来看看四种变换的具体情形。由于所有的图形都是有点组成，因此我们只需要考察一个点相关变换即可。

一、 平移变换

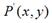假定有一个点的坐标是 ，将其移动到 ，再假定在x轴和y轴方向移动的大小分别为：

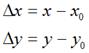
如下图所示：

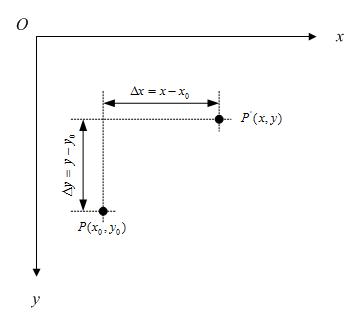
不难知道：

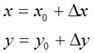
如果用矩阵来表示的话，就可以写成：

 

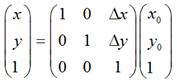
二、 旋转变换

2.1    围绕坐标原点旋转：

假定有一个点 ，相对坐标原点顺时针旋转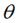后的情形，同时假定P点离坐标原点的距离为r，如下图：

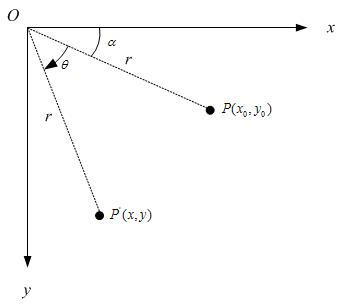
那么，

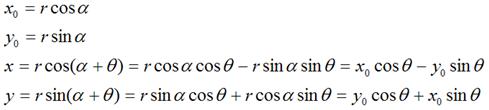
如果用矩阵，就可以表示为：

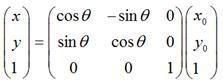
2.2    围绕某个点旋转

如果是围绕某个点顺时针旋转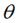，那么可以用矩阵表示为：

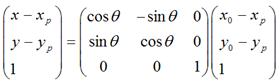
可以化为：

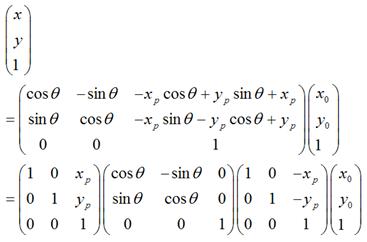
很显然，

1.

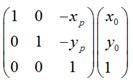是将坐标原点移动到点后， 的新坐标。

2.

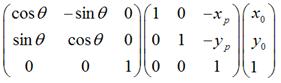
是将上一步变换后的，围绕新的坐标原点顺时针旋转 。

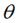3.

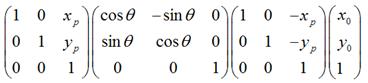
经过上一步旋转变换后，再将坐标原点移回到原来的坐标原点。

所以，围绕某一点进行旋转变换，可以分成3个步骤，即首先将坐标原点移至该点，然后围绕新的坐标原点进行旋转变换，再然后将坐标原点移回到原先的坐标原点。

三、 缩放变换

理论上而言，一个点是不存在什么缩放变换的，但考虑到所有图像都是由点组成，因此，如果图像在x轴和y轴方向分别放大k1和k2倍的话，那么图像中的所有点的x坐标和y坐标均会分别放大k1和k2倍，即

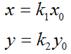
用矩阵表示就是：

缩放变换比较好理解，就不多说了。

四、 错切变换

错切变换(skew)在数学上又称为Shear mapping(可译为“剪切变换”)或者Transvection(缩并)，它是一种比较特殊的线性变换。错切变换的效果就是让所有点的x坐标(或者y坐标)保持不变，而对应的y坐标(或者x坐标)则按比例发生平移，且平移的大小和该点到x轴(或y轴)的垂直距离成正比。错切变换，属于等面积变换，即一个形状在错切变换的前后，其面积是相等的。

比如下图，各点的y坐标保持不变，但其x坐标则按比例发生了平移。这种情况将水平错切。

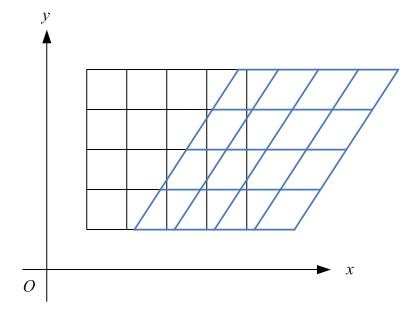
下图各点的x坐标保持不变，但其y坐标则按比例发生了平移。这种情况叫垂直错切。

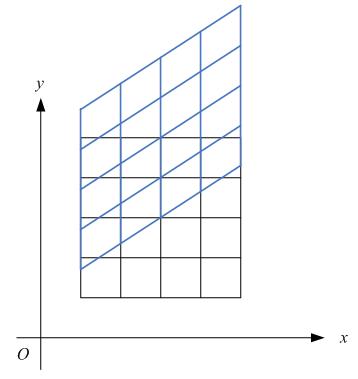
假定一个点经过错切变换后得到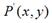，对于水平错切而言，应该有如下关系：

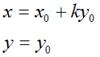
用矩阵表示就是：

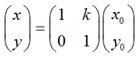
扩展到3 x 3的矩阵就是下面这样的形式：

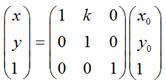
同理，对于垂直错切，可以有：

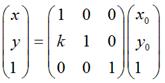
在数学上严格的错切变换就是上面这样的。在Android中除了有上面说到的情况外，还可以同时进行水平、垂直错切，那么形式上就是：

五、 对称变换

除了上面讲到的4中基本变换外，事实上，我们还可以利用Matrix，进行对称变换。所谓对称变换，就是经过变化后的图像和原图像是关于某个对称轴是对称的。比如，某点 经过对称变换后得到，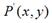

如果对称轴是x轴，难么，

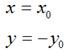
用矩阵表示就是：

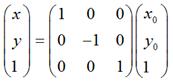
如果对称轴是y轴，那么，

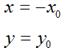
用矩阵表示就是：

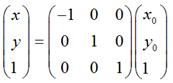
如果对称轴是y = x，如图：

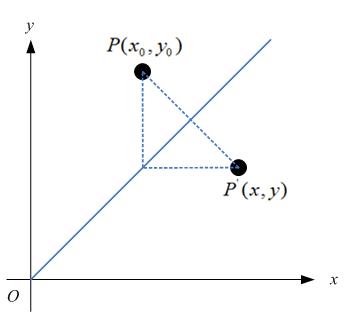
那么，

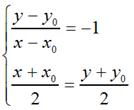
很容易可以解得：

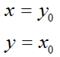
用矩阵表示就是：

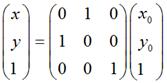
同样的道理，如果对称轴是y = -x，那么用矩阵表示就是：

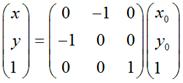
特殊地，如果对称轴是y = kx，如下图：

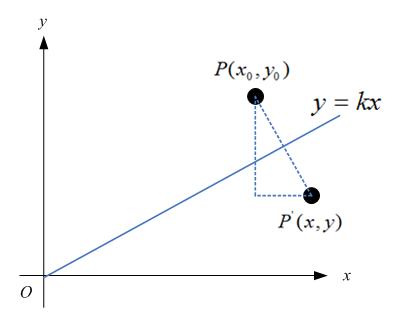
那么，

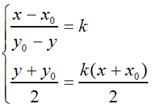
很容易可解得：

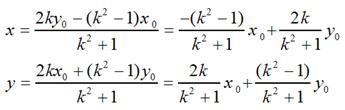
用矩阵表示就是：

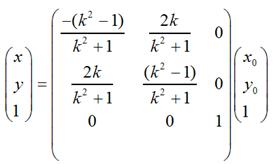
当k = 0时，即y = 0，也就是对称轴为x轴的情况；当k趋于无穷大时，即x = 0，也就是对称轴为y轴的情况；当k =1时，即y = x，也就是对称轴为y = x的情况；当k = -1时，即y = -x，也就是对称轴为y = -x的情况。不难验证，这和我们前面说到的4中具体情况是相吻合的。

如果对称轴是y = kx + b这样的情况，只需要在上面的基础上增加两次平移变换即可，即先将坐标原点移动到(0, b)，然后做上面的关于y = kx的对称变换，再然后将坐标原点移回到原来的坐标原点即可。用矩阵表示大致是这样的：

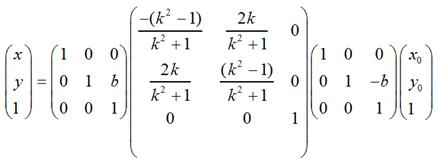
需要特别注意：在实际编程中，我们知道屏幕的y坐标的正向和数学中y坐标的正向刚好是相反的，所以在数学上y = x和屏幕上的y = -x才是真正的同一个东西，反之亦然。也就是说，如果要使图片在屏幕上看起来像按照数学意义上y = x对称，那么需使用这种转换：

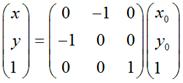
要使图片在屏幕上看起来像按照数学意义上y = -x对称，那么需使用这种转换：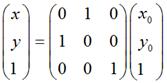

关于对称轴为y = kx 或y = kx + b的情况，同样需要考虑这方面的问题。

 

附：三角函数公式 ，有助于理解Matrix原理

两角和公式

sin(a+b)=sinacosb+cosasinb

sin(a-b)=sinacosb-sinbcosa 

cos(a+b)=cosacosb-sinasinb

cos(a-b)=cosacosb+sinasinb

tan(a+b)=(tana+tanb)/(1-tanatanb)

tan(a-b)=(tana-tanb)/(1+tanatanb)

cot(a+b)=(cotacotb-1)/(cotb+cota) 

cot(a-b)=(cotacotb+1)/(cotb-cota)

倍角公式

tan2a=2tana/[1-(tana)^2]

cos2a=(cosa)^2-(sina)^2=2(cosa)^2 -1=1-2(sina)^2

sin2a=2sina*cosa

半角公式

sin(a/2)=√((1-cosa)/2) sin(a/2)=-√((1-cosa)/2)

cos(a/2)=√((1+cosa)/2) cos(a/2)=-√((1+cosa)/2)

tan(a/2)=√((1-cosa)/((1+cosa)) tan(a/2)=-√((1-cosa)/((1+cosa))

cot(a/2)=√((1+cosa)/((1-cosa)) cot(a/2)=-√((1+cosa)/((1-cosa)) 

tan(a/2)=(1-cosa)/sina=sina/(1+cosa)

和差化积

2sinacosb=sin(a+b)+sin(a-b)

2cosasinb=sin(a+b)-sin(a-b) )

2cosacosb=cos(a+b)-sin(a-b)

-2sinasinb=cos(a+b)-cos(a-b)

sina+sinb=2sin((a+b)/2)cos((a-b)/2

cosa+cosb=2cos((a+b)/2)sin((a-b)/2)

tana+tanb=sin(a+b)/cosacosb

积化和差公式

sin(a)sin(b)=-1/2*[cos(a+b)-cos(a-b)]

cos(a)cos(b)=1/2*[cos(a+b)+cos(a-b)]

sin(a)cos(b)=1/2*[sin(a+b)+sin(a-b)]

诱导公式

sin(-a)=-sin(a)

cos(-a)=cos(a)

sin(pi/2-a)=cos(a)

cos(pi/2-a)=sin(a)

sin(pi/2+a)=cos(a)

cos(pi/2+a)=-sin(a)

sin(pi-a)=sin(a)

cos(pi-a)=-cos(a)

sin(pi+a)=-sin(a)

cos(pi+a)=-cos(a)

tga=tana=sina/cosa

万能公式

sin(a)= (2tan(a/2))/(1+tan^2(a/2))

cos(a)= (1-tan^2(a/2))/(1+tan^2(a/2))

tan(a)= (2tan(a/2))/(1-tan^2(a/2))

其它公式

a*sin(a)+b*cos(a)=sqrt(a^2+b^2)sin(a+c) [其中，tan(c)=b/a]

a*sin(a)-b*cos(a)=sqrt(a^2+b^2)cos(a-c) [其中，tan(c)=a/b]

1+sin(a)=(sin(a/2)+cos(a/2))^2

1-sin(a)=(sin(a/2)-cos(a/2))^2

其他非重点三角函数

csc(a)=1/sin(a)

sec(a)=1/cos(a)