并查集(加权) LA 4487 Exclusive-OR

题目传送门

题意：训练指南P245

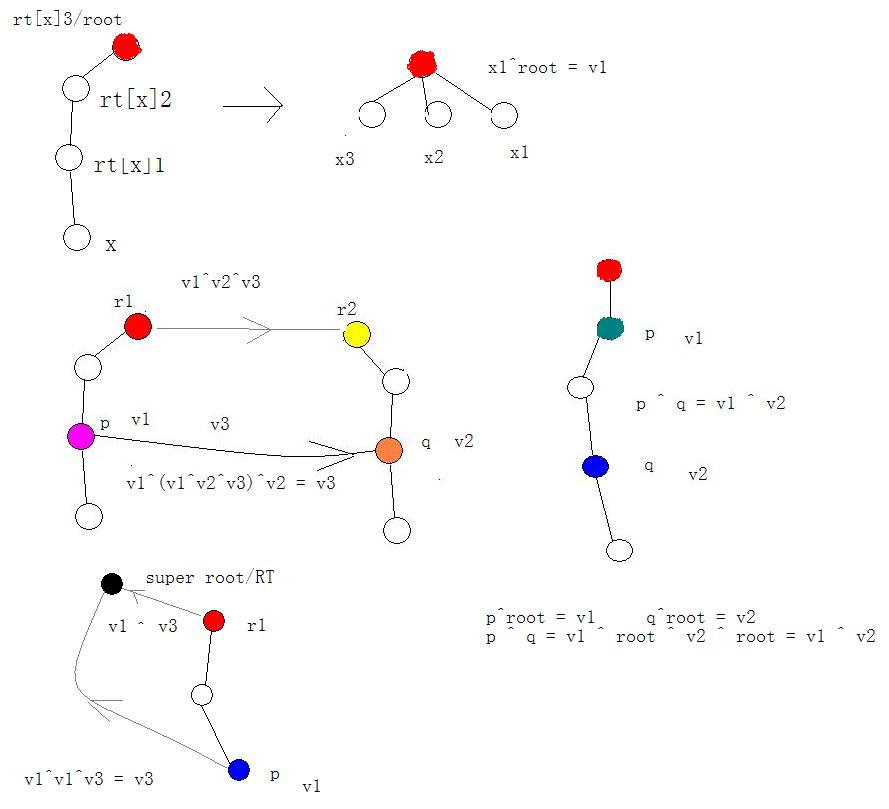
分析：首先这道是经典的并查集题目，利用异或的性质。异或性质：x ^ 0 = x -> a ^ a = 0 -> x ^ a ^ a = x，即一个数对某个数异或偶数次等于它本身。

第一种操作：p = v，设立一个超级根节点RT，rt[p] = RT, edge[p] = v，表示p的父亲节点是RT，到它的值就是p本身的值(p^0)。第二种p q v操作，分别找p和q的祖先，将祖先合并，那么edge[r1] = v1 ^ v2 ^ v3，这样保证下一次v1'仍然是p到祖先的异或值，这样p ^ q = p ^ root' ^ q ^ root' = v1'^v2’。第三种操作，如果pi的祖先是RT，那么v1就是p的值，否则v1 = p ^ rootp，这样需要同一个祖先的个数是偶数才能将祖先的影响取消。

#include <bits/stdc++.h>
using namespace std;

const int N = 2e4 + 5;
const int Q = 4e4 + 5;
struct DSU  {
    int rt[N], edge[N];
    void clear(void)    {
        memset (rt, -1, sizeof (rt));
    }
    int Find(int x, int &val) {
        if (rt[x] == -1)    {
            val = 0;    return x;
        }
        int root = Find (rt[x], val);
        val ^= edge[x];
        edge[x] = val;
        rt[x] = root;
        return root;
    }
    void Union(int x, int y, int val)    {
        if (x > y)  swap (x, y);
        rt[x] = y;  edge[x] = val;
    }
}dsu;
int id[N], RT;

void error(int fac) {
    printf ("The first %d facts are conflicting.\n", fac);
}

int main(void)  {
    int n, m, cas = 0;
    while (scanf ("%d%d", &n, &m) == 2) {
        if (!n && !m)   break;
        printf ("Case %d:\n", ++cas);
        RT = n;     //super root
        dsu.clear ();
        bool err = false;
        char str[30];    int p, q, k, v1, v2, v3, r1, r2;
        int facts = 0;
        for (int i=1; i<=m; ++i)    {
            scanf ("%s", &str);
            if (str[0] == 'I')   {
                facts++;
                gets (str);
                if (err)    continue;
                if (sscanf (str, "%d %d %d", &p, &q, &v3) == 2)  {
                    v3 = q;
                    int r1 = dsu.Find (p, v1);
                    if (r1 == RT)    {        //super tree
                        if (v1 != v3)   {
                            error (facts);  err = true;
                        }
                    }
                    else    {
                        dsu.Union (r1, RT, v1 ^ v3);
                    }
                }
                else    {
                    int r1 = dsu.Find (p, v1);
                    int r2 = dsu.Find (q, v2);
                    if (r1 == r2)   {       //in the same tree
                        if ((v1 ^ v2) != v3)    {
                            error (facts);  err = true;
                        }
                    }
                    else    dsu.Union (r1, r2, v1 ^ v2 ^ v3);       //cat r1 and r2
                }
            }
            else    {
                scanf ("%d", &k);
                for (int j=1; j<=k; ++j)    {
                    scanf ("%d", &id[j]);
                }
                if (err)    continue;
                int ans = 0;
                vector<int> rs;
                for (int j=1; j<=k; ++j)    {
                    int r1 = dsu.Find (id[j], v1);
                    ans ^= v1;
                    if (r1 != RT)   {
                        rs.push_back (r1);
                    }
                }
                if (rs.size () % 2 == 1)    {
                    printf ("I don't know.\n");
                }
                else    {
                    sort (rs.begin (), rs.end ());
                    for (int j=0; j<rs.size (); j+=2)    {
                        if (rs[j] != rs[j+1])   {
                            ans = -1;   break;
                        }
                    }
                    if (ans == -1)    {
                        printf ("I don't know.\n");
                    }
                    else    printf ("%d\n", ans);
                }
            }
        }
        puts ("");
    }

    return 0;
}