poj2284 欧拉公式

题意：给出一图形，求该图形把平面分成了几部分

欧拉公式：　　http://blog.csdn.net/wangxiaojun911/article/details/4586550

对于二维平面上的情况。设图形上有V个点，E条边，把平面分成了F个独立的部分，那么满足V+F-E=2

如下图：

             

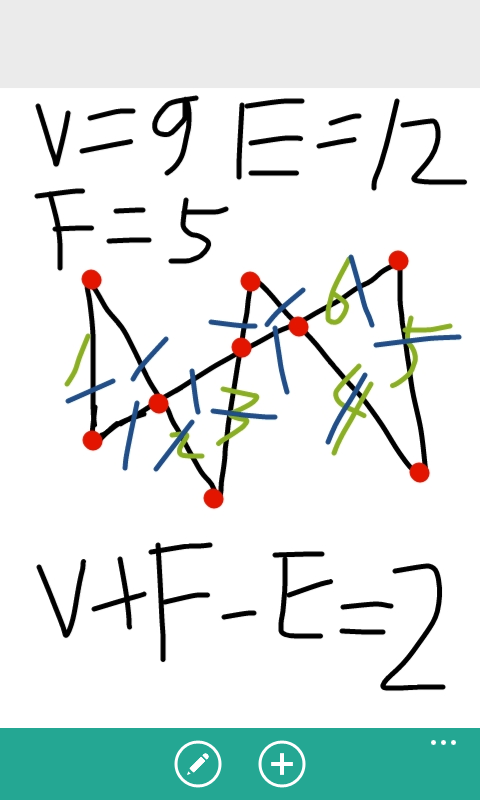
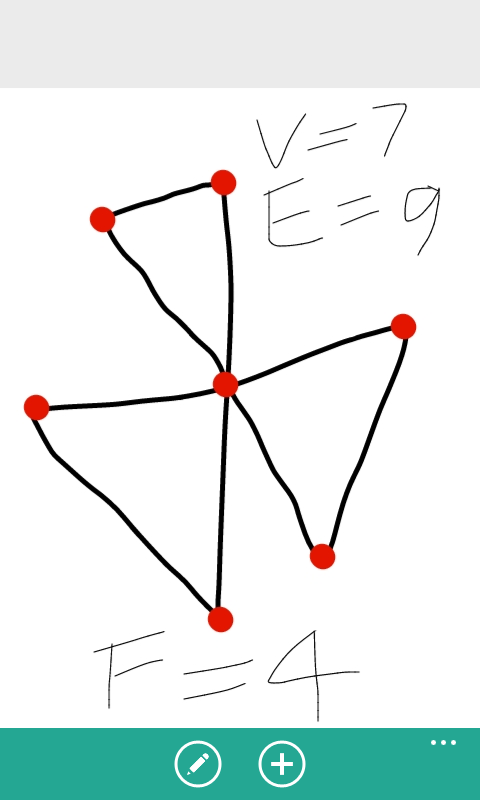
那么求F就转化成了如何求V和E

求V：枚举任意两线段的交点即可。注意可能出现三线共点的情况，要判重。

求E：某线段上的n个点会把这条线段分成n-1部分。用这个性质再YY一下就好了。

注意：

1.这里判重不能用map，因为交点的计算结果肯定是有精度误差的，再hash一下就没法判重了。

　　我用的方法是手艹了一个破vector，实际上有更简洁的方法.....

先排序，使重复的元素在数组里相邻。再用STL里的unique即可轻松实现去重

（ Reference：http://blog.sina.com.cn/s/blog_a389f34a01013itn.html）

2.模板里的求两线段交点代码没有考虑这种情况：

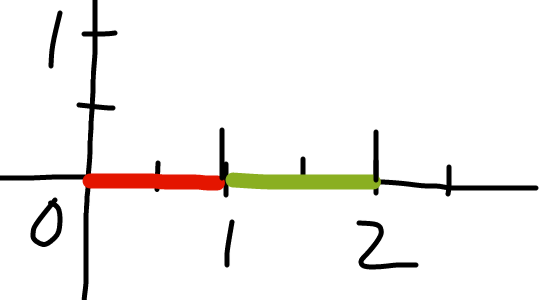
如图，两线段分别为【(0,0)->(0,1)】和【(0,1)->(0,2)】

模板代码认为他们是不香蕉的= =  哼

所以这里要处理一下：

（大白书上lrj模板也存在这个问题）

    //求两线交点
    point crosspoint(line v)
    {
        if ((point_cmp(a,v.a))||(point_cmp(a,v.b)))     return a;
        if ((point_cmp(b,v.a))||(point_cmp(b,v.b)))     return b;        //处理端点处相交的情况
        double a1=v.b.sub(v.a).det(a.sub(v.a));
        double a2=v.b.sub(v.a).det(b.sub(v.a));
        return point((a.x*a2-b.x*a1)/(a2-a1),(a.y*a2-b.y*a1)/(a2-a1));
    }

AC  Code：

 #include<vector>
 #include<list>
 #include<map>
 #include<set>
 #include<deque>
 #include<queue>
 #include<stack>
 #include<bitset>
 #include<algorithm>
 #include<functional>
 #include<numeric>
 #include<utility>
 #include<iostream>
 #include<sstream>
 #include<iomanip>
 #include<cstdio>
 #include<cmath>
 #include<cstdlib>
 #include<cctype>
 #include<string>
 #include<cstring>
 #include<cstdio>
 #include<cmath>
 #include<cstdlib>
 #include<ctime>
 #include<climits>
 #include<complex>
 #define mp make_pair
 #define pb push_back
 using namespace std;
 const double eps=1e-;//精度
 const double pi=acos(-1.0);//π
 const double inf=1e20;//无穷大
 const int maxp=;//最大点数
 /*
     判断d是否在精度内等于0
 */
 int dblcmp(double d)
 {
     if (fabs(d)<eps)return ;
     return d>eps?:-;
 }
 
 bool dcmp(double x)
 {
     return (fabs(x)<eps);
 }
 
 /*
     求x的平方
 */
 inline double sqr(double x){return x*x;}
 /*
     点/向量
 */
 struct point
 {
     double x,y;
     point(){}
     point(double _x,double _y):x(_x),y(_y){};
     //读入一个点
     void input()
     {
         scanf("%lf%lf",&x,&y);
     }
     //输出一个点
     void output()
     {
         printf("%.2f %.2f\n",x,y);
     }
     //判断两点是否相等
     bool operator==(point a)const
     {
         return dblcmp(a.x-x)==&&dblcmp(a.y-y)==;
     }
     //判断两点大小
     bool operator<(point a)const
     {
         return dblcmp(a.x-x)==?dblcmp(y-a.y)<:x<a.x;
     }
     //点到源点的距离/向量的长度
     double len()
     {
         return hypot(x,y);
     }
     //点到源点距离的平方
     double len2()
     {
         return x*x+y*y;
     }
     //两点间的距离
     double distance(point p)
     {
         return hypot(x-p.x,y-p.y);
     }
     //向量加
     point add(point p)
     {
         return point(x+p.x,y+p.y);
     }
     //向量减
     point sub(point p)
     {
         return point(x-p.x,y-p.y);
     }
     //向量乘
     point mul(double b)
     {
         return point(x*b,y*b);
     }
     //向量除
     point div(double b)
     {
         return point(x/b,y/b);
     }
     //点乘
     double dot(point p)
     {
         return x*p.x+y*p.y;
     }
     //叉乘
     double det(point p)
     {
         return x*p.y-y*p.x;
     }
     //XXXXXXX
     double rad(point a,point b)
     {
         point p=*this;
         return fabs(atan2(fabs(a.sub(p).det(b.sub(p))),a.sub(p).dot(b.sub(p))));
     }
     //截取长度r
     point trunc(double r)
     {
         double l=len();
         if (!dblcmp(l))return *this;
         r/=l;
         return point(x*r,y*r);
     }
     //左转90度
     point rotleft()
     {
         return point(-y,x);
     }
     //右转90度
     point rotright()
     {
         return point(y,-x);
     }
     //绕点p逆时针旋转angle角度
     point rotate(point p,double angle)
     {
         point v=this->sub(p);
         double c=cos(angle),s=sin(angle);
         return point(p.x+v.x*c-v.y*s,p.y+v.x*s+v.y*c);
     }
 };
 
 bool point_cmp(point a,point b)
 {
     return ((dcmp(a.x-b.x))&&(dcmp(a.y-b.y)));
 }
 
 /*
     线段/直线
 */
 struct line
 {
     point a,b;
     line(){}
     line(point _a,point _b)
     {
         a=_a;
         b=_b;
     }
     //判断线段相等
     bool operator==(line v)
     {
         return (a==v.a)&&(b==v.b);
     }
     //点p做倾斜角为angle的射线
     line(point p,double angle)
     {
         a=p;
         if (dblcmp(angle-pi/)==)
         {
             b=a.add(point(,));
         }
         else
         {
             b=a.add(point(,tan(angle)));
         }
     }
     //直线一般式ax+by+c=0
     line(double _a,double _b,double _c)
     {
         if (dblcmp(_a)==)
         {
             a=point(,-_c/_b);
             b=point(,-_c/_b);
         }
         else if (dblcmp(_b)==)
         {
             a=point(-_c/_a,);
             b=point(-_c/_a,);
         }
         else
         {
             a=point(,-_c/_b);
             b=point(,(-_c-_a)/_b);
         }
     }
     //读入一个线段
     void input()
     {
         a.input();
         b.input();
     }
     //校准线段两点
     void adjust()
     {
         if (b<a)swap(a,b);
     }
     //线段长度
     double length()
     {
         return a.distance(b);
     }
     //直线倾斜角 0<=angle<180
     double angle()
     {
         double k=atan2(b.y-a.y,b.x-a.x);
         if (dblcmp(k)<)k+=pi;
         if (dblcmp(k-pi)==)k-=pi;
         return k;
     }
     //点和线段关系
     //1 在逆时针
     //2 在顺时针
     //3 平行
     int relation(point p)
     {
         int c=dblcmp(p.sub(a).det(b.sub(a)));
         if (c<)return ;
         if (c>)return ;
         return ;
     }
     //点是否在线段上
     bool pointonseg(point p)
     {
         //if ((p==a) || (p==b))  return true;
         return dblcmp(p.sub(a).det(b.sub(a)))==&&dblcmp(p.sub(a).dot(p.sub(b)))<=;
     }
     //两线是否平行
     bool parallel(line v)
     {
         return dblcmp(b.sub(a).det(v.b.sub(v.a)))==;
     }
     //线段和线段关系
     //0 不相交
     //1 非规范相交
     //2 规范相交
     int segcrossseg(line v)
     {
         int d1=dblcmp(b.sub(a).det(v.a.sub(a)));
         int d2=dblcmp(b.sub(a).det(v.b.sub(a)));
         int d3=dblcmp(v.b.sub(v.a).det(a.sub(v.a)));
         int d4=dblcmp(v.b.sub(v.a).det(b.sub(v.a)));
         if ((d1^d2)==-&&(d3^d4)==-)return ;
         return (d1==&&dblcmp(v.a.sub(a).dot(v.a.sub(b)))<=||
                 d2==&&dblcmp(v.b.sub(a).dot(v.b.sub(b)))<=||
                 d3==&&dblcmp(a.sub(v.a).dot(a.sub(v.b)))<=||
                 d4==&&dblcmp(b.sub(v.a).dot(b.sub(v.b)))<=);
     }
     //线段和直线v关系
     int linecrossseg(line v)//*this seg v line
     {
         int d1=dblcmp(b.sub(a).det(v.a.sub(a)));
         int d2=dblcmp(b.sub(a).det(v.b.sub(a)));
         if ((d1^d2)==-)return ;
         return (d1==||d2==);
     }
     //直线和直线关系
     //0 平行
     //1 重合
     //2 相交
     int linecrossline(line v)
     {
         if ((*this).parallel(v))
         {
             return v.relation(a)==;
         }
         return ;
     }
     //求两线交点
     point crosspoint(line v)
     {
         if ((point_cmp(a,v.a))||(point_cmp(a,v.b)))     return a;
         if ((point_cmp(b,v.a))||(point_cmp(b,v.b)))     return b;
         double a1=v.b.sub(v.a).det(a.sub(v.a));
         double a2=v.b.sub(v.a).det(b.sub(v.a));
         return point((a.x*a2-b.x*a1)/(a2-a1),(a.y*a2-b.y*a1)/(a2-a1));
     }
 
     //点p到直线的距离
     double dispointtoline(point p)
     {
         return fabs(p.sub(a).det(b.sub(a)))/length();
     }
     //点p到线段的距离
     double dispointtoseg(point p)
     {
         if (dblcmp(p.sub(b).dot(a.sub(b)))<||dblcmp(p.sub(a).dot(b.sub(a)))<)
         {
             return min(p.distance(a),p.distance(b));
         }
         return dispointtoline(p);
     }
     //XXXXXXXX
     point lineprog(point p)
     {
         return a.add(b.sub(a).mul(b.sub(a).dot(p.sub(a))/b.sub(a).len2()));
     }
     //点p关于直线的对称点
     point symmetrypoint(point p)
     {
         point q=lineprog(p);
         return point(*q.x-p.x,*q.y-p.y);
     }
 };
 
 struct point P[];
 struct line  L[];
 int n;
 int CASE=;
 
 int main()
 {
     //freopen("in.txt","r",stdin);
 
     while (cin>>n)
     {
         if (n==)   break;
         {
             CASE++;
             n--;
             for (int i=;i<=n+;i++)
             {
                 scanf("%lf%lf",&P[i].x,&P[i].y);
                 if (i>=)
                     L[i-]=line(point(P[i-].x,P[i-].y),point(P[i].x,P[i].y));
             }
             //L[1..n]:line      P[1..n]:point   P[1]==P[n+1]
 
             vector<point> POINT;
             POINT.clear();
 
             int pcount=;       //the number of points
             for (int i=;i<n;i++)
                 for (int j=i+;j<=n;j++)
                 {
                     if (L[i].segcrossseg(L[j])!=)
                     {
                         point tm=L[i].crosspoint(L[j]);
                         //printf("P:   %.3f   %.3f\n",tm.x,tm.y);
                         bool Find=false;
                         for (vector<point>::iterator it=POINT.begin();it!=POINT.end();it++)
                         {
                             point tp=*it;
                             if ((dcmp(tp.x-tm.x))&&(dcmp(tp.y-tm.y)))
                                 Find=true;
                         }
                         if (!Find)
                         {
                             pcount++;
                             POINT.push_back(tm);
                         }
                     }
                 }
 
             for (vector<point>::iterator it=POINT.begin();it!=POINT.end();it++)
             {
                 point tp=*it;
                 //printf("%.5f %.5f\n",tp.x,tp.y);
             }
 
             int lcount=;
             for (int i=;i<=n;i++)
             {
                 line tm=L[i];
                 int tmp=;
                 for (vector<point>::iterator it=POINT.begin();it!=POINT.end();it++)
                 {
                     point tp=*it;
                     if (tm.pointonseg(tp))
                         tmp++;
                 }
                 lcount=lcount+(tmp-);
             }
 
             //cout<<pcount<<"   "<<lcount<<endl;
             //cout<<2+lcount-pcount<<endl;
             //Case 1: There are 2 pieces.
             int ans=+lcount-pcount;
             //if (ans<0)  ans=2;
             printf("Case %d: There are %d pieces.\n",CASE,ans);
         }
     }
 
     return ;
 }

PS：在poj discussion里面有人给出了这样一组数据:

4

0 0 0 1 0 2 0 0　　　　

答案为2

这组数据我过不去 ╮(╯▽╰)╭

不过这种情况本身就够坑的，所以也不影响AC啦 ╮(╯▽╰)╭