P3368 【模板】树状数组 2--洛谷luogu

题目描述

如题，已知一个数列，你需要进行下面两种操作：

1.将某区间每一个数数加上x

2.求出某一个数的值

输入输出格式

输入格式：

第一行包含两个整数N、M，分别表示该数列数字的个数和操作的总个数。

第二行包含N个用空格分隔的整数，其中第i个数字表示数列第i项的初始值。

接下来M行每行包含2或4个整数，表示一个操作，具体如下：

操作1： 格式：1 x y k 含义：将区间[x,y]内每个数加上k

操作2： 格式：2 x 含义：输出第x个数的值

输出格式：

输出包含若干行整数，即为所有操作2的结果。

输入输出样例

输入样例#1： 复制

5 5
1 5 4 2 3
1 2 4 2
2 3
1 1 5 -1
1 3 5 7
2 4

输出样例#1： 复制

6
10

说明

时空限制：1000ms,128M

数据规模：

对于30%的数据：N<=8，M<=10

对于70%的数据：N<=10000，M<=10000

对于100%的数据：N<=500000，M<=500000

样例说明：

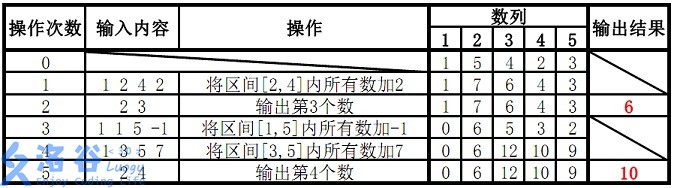
故输出结果为6、10

---------------------------------------------------------------------------------------------------------------------------------------------------

模板题就是模板题

不按它的思路走就是不行啊

一上来

我就想到了小暴力

把x到y之间全算一遍

然而

毫无疑问

tle了

于是我去看了题解

没错用到了我没有的

差分

---------------------------------------------------------------------------------------------------------------------------------------------------

差分：

设数组a[]={1,6,8,5,10}，那么差分数组b[]={1,5,2,-3,5}

也就是说b[i]=a[i]-a[i-1];(a[0]=0;)，那么a[i]=b[1]+....+b[i];(这个很好证的)。

假如区间[2,4]都加上2的话

a数组变为a[]={1,8,10,7,10}，b数组变为b={1,7,2,-3,3};

发现了没有，b数组只有b[2]和b[5]变了，因为区间[2,4]是同时加上2的,所以在区间内b[i]-b[i-1]是不变的.

所以对区间[x,y]进行修改,只用修改b[x]与b[y+1]:

b[x]=b[x]+k;b[y+1]=b[y+1]-k;

#include <cstdio>
#define lowbit(x) x & -x

using namespace std;

int tree[];
int n, m;

void add(int x,int num)
{
    while (x <= n)
    {
        tree[x] += num;
        x += lowbit(x);
    }
}

int query(int x)
{
    int ans = ;
    while (x)
    {
        ans += tree[x];
        x -= lowbit(x);
    }
    return ans;
}

int main()
{
    scanf("%d%d", &n, &m);
    int last = , now;
    for (int i = ; i <= n; i++)
    {
        scanf("%d", &now);
        add(i, now - last);
        last = now;
    }
    int flg;
    while (m--)
    {
        scanf("%d", &flg);
        if (flg == )
        {
            int x, y;
            int k;
            scanf("%d%d%d", &x, &y, &k);
            add(x, k);
            add(y + , -k);
        } else
        if (flg == )
        {
            int x;
            scanf("%d", &x);
            printf("%d\n", query(x));
        }
    }
    return ;
}