索引堆（Index Heap）

首先我们先来看一个由普通数组构建的普通堆。

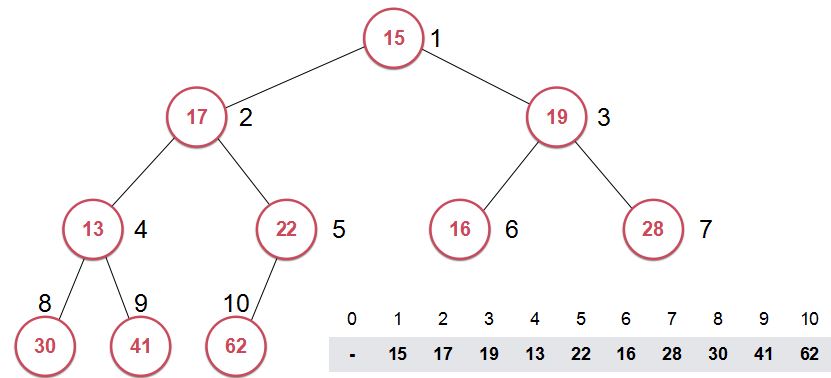
然后我们通过前面的方法对它进行堆化（heapify），将其构建为最大堆。

结果是这样的：

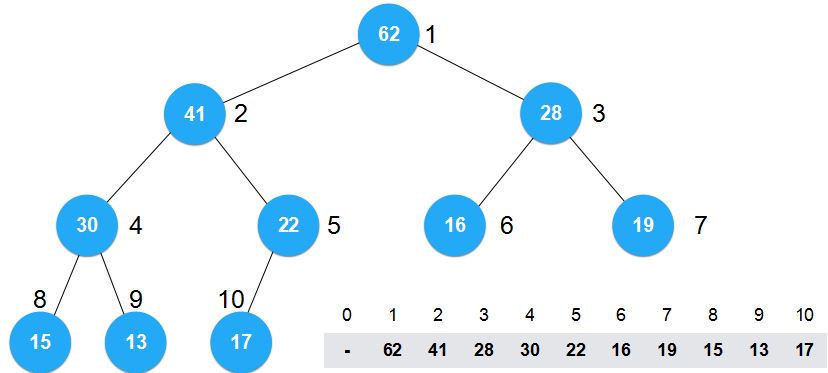
对于我们所关心的这个数组而言，数组中的元素位置发生了改变。正是因为这些元素的位置发生了改变，我们才能将其构建为最大堆。

可是由于数组中元素位置的改变，我们将面临着几个局限性。

1.如果我们的元素是十分复杂的话，比如像每个位置上存的是一篇10万字的文章。那么交换它们之间的位置将产生大量的时间消耗。（不过这可以通过技术手段解决）

2.由于我们的数组元素的位置在构建成堆之后发生了改变，那么我们之后就很难索引到它，很难去改变它。例如我们在构建成堆后，想去改变一个原来元素的优先级（值），将会变得非常困难。

可能我们在每一个元素上再加上一个属性来表示原来位置可以解决，但是这样的话，我们必须将这个数组遍历一下才能解决。（性能低效）

---

针对以上问题，我们就需要引入索引堆（Index Heap）的概念。

对于索引堆来说，我们将数据和索引这两部分分开存储。真正表征堆的这个数组是由索引这个数组构建成的。（像下图中那样，每个结点的位置写的是索引号）

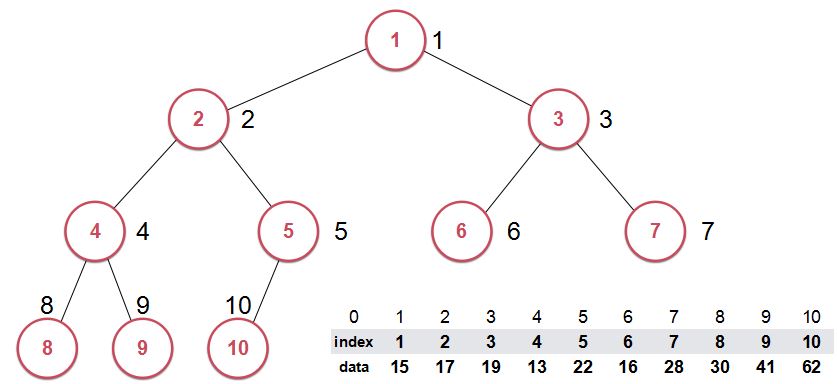
而在构建堆（以最大索引堆为例）的时候，比较的是data中的值（即原来数组中对应索引所存的值），构建成堆的却是index域

而构建完之后，data域并没有发生改变，位置改变的是index域。

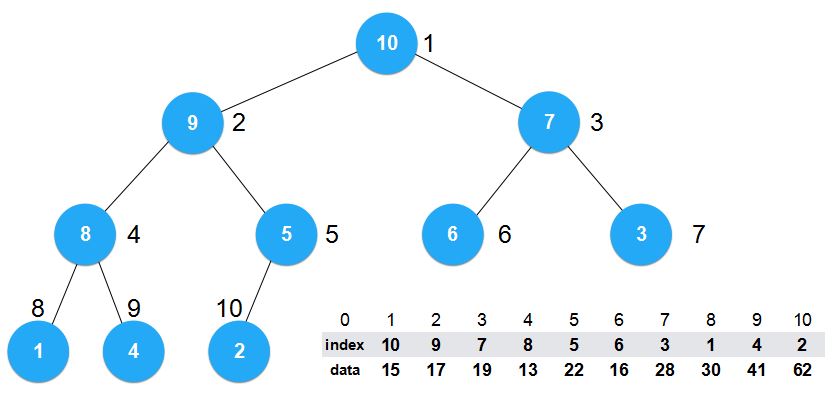
那么现在这个最大堆该怎么解读呢？

例如，堆顶元素为Index=10代表的就是索引为10的data域的值，即62。

这时我们来看，构建堆的过程就是简单地索引之间的交换，索引就是简单的int型。效率很高。

现在如果我们想对这个数组进行一些改变，比如我们想将索引为7的元素值改为100，那我们需要做的就是将索引7所对应data域的28改为100。时间复杂度为O（1）。

当然改完之后，我们还需要进行一些操作来维持最大堆的性质。不过调整的过程改变的依旧是index域的内容。

代码：

package com.heap;

public class IndexMaxHeap {

    private int[] arr;
    private int[] index;
    private int count;
    private int capacity;

    //构造方法
    public IndexMaxHeap(int capacity){
        this.capacity=capacity;
        this.count=0;//数量初始化为0
        arr=new int[capacity+1];//索引从0开始
        index=new int[capacity+1];
    } 

    //判断当前堆是否为空
        public Boolean isEmpty(){
            return count==0;
        }

        //返回该最大堆的元素个数
        public int size(){
            return count;
        }

        //插入元素到最大堆
        public void insertItem(int item){
            if(count+1>capacity)
                System.out.println("容量已满，插入失败");
            else
            {
                count++;
                arr[count]=item;
                index[count]=count;

                //向上调整
                shiftUp(count);
            }
        }

        //向上调整
    private void shiftUp(int k) {
        //比较的是arr数组
        //注意此时堆中存储的是index值，比较的是对应index值对应的arr[]数组的值
        if(k>1&&arr[index[k/2]]<arr[index[k]]){
            //交换的是index数组
            int temp=index[k/2];
            index[k/2]=index[k];
            index[k]=temp;

        }else
            return;

        k=k/2;
        shiftUp(k);

        }

    //从堆里取出堆顶元素
    public int extractMax(){
        if(count<1){
            System.out.println("该最大堆为空");
            return -1;
        }else
        {
            //这里取出来的是arr[]数组中的元素
            //这里调整的还是index
            int item=arr[index[1]];
            //将末尾元素放到堆顶
            index[1]=index[count];
            count--;//堆的元素个数减一

            //向下调整元素
            shiftDown(1);

          return item;
        }

    }

    //向下调整元素
    private void shiftDown(int k) {
        //如果这个结点有左孩子
        while(2*k<=count){
            int j=2*k;
            if(j+1<=count&&arr[index[j+1]]>arr[index[j]])
                j+=1;
            if(arr[index[j]]>arr[index[k]]){
                int temp=index[j];
                index[j]=index[k];
                index[k]=temp;

                k=j;
            }else
                break;
        }

    }

    //取出最大元素的索引值
    public int getMaxIndex(){
        return index[1];
    }

    //返回给定索引在堆中所处位置对应的数据值
    public int getItemByIndex(int i){
        return arr[index[i]];
    }

    //改变给定索引对应的数据值
    //别忘了改变完数据值，再去调整一下整个堆的形态
    public void change(int i,int newValue){
        arr[i]=newValue;//修改指定索引对应的值

        //要调整改变完值的堆，必须先找到当前这个指定索引所对应的数据在堆中的位置
        //我们知道在插入堆时，我们调整的是index域的位置变化，那么对应的index[j]的值就应该是i（即数组本来的索引）
        //我们遍历一下index域就能找到index[j]==i;j就表示arr[i]在堆中的位置
        for(int j=1;j<=count;j++){
            if(index[j]==i){
                //试着往上调一调，再试着往下调一调。就完成了堆的调整
                shiftUp(j);
                shiftDown(j);

                return;//跳出多余循环
            }
        }
    } 

    public static void main(String[] args) {
        IndexMaxHeap heap=new IndexMaxHeap(100);
        heap.insertItem(3);
        heap.insertItem(15);
        heap.insertItem(23);
        heap.insertItem(7);
        heap.insertItem(4);
        heap.insertItem(8);
        System.out.println("堆的大小"+heap.size());
        System.out.println("堆顶元素的索引值"+heap.getMaxIndex());
        System.out.println("返回索引2的值："+heap.getItemByIndex(2));
        System.out.println("按堆的顺序输出元素：");
        for(int i=1;i<=heap.count;i++)
            System.out.print(heap.getItemByIndex(i)+" ");
        System.out.println();
        heap.change(3, 66);
        System.out.println("按堆的顺序输出元素：");
        for(int i=1;i<=heap.count;i++)
            System.out.print(heap.getItemByIndex(i)+" ");
        System.out.println();
        System.out.println("此时堆顶元素"+heap.extractMax());
        System.out.println("此时堆顶元素"+heap.extractMax());
        System.out.println("此时堆顶元素"+heap.extractMax());
        System.out.println("此时堆顶元素"+heap.extractMax());
        System.out.println("堆的大小"+heap.size());

    }

}

和堆相关的问题

---

1）使用堆来实现优先队列

动态选择优先级最高的任务执行。

2）实现多路归并排序

将整个数组分成n个子数组，子数组排完序之后，将每个子数组中最小的元素取出，放到一个最小堆里面，每次从最小堆里取出最小值放到归并结束的数组中，被取走的元素属于哪个子数组，就从哪个子数组中再取出一个补充到最小堆里面，如此循环，直到所有子数组归并到一个数组中。