强化学习（四）—— DQN系列（DQN, Nature DQN, DDQN, Dueling DQN等）

1 概述

　　在之前介绍的几种方法，我们对值函数一直有一个很大的限制，那就是它们需要用表格的形式表示。虽说表格形式对于求解有很大的帮助，但它也有自己的缺点。如果问题的状态和行动的空间非常大，使用表格表示难以求解，因为我们需要将所有的状态行动价值求解出来，才能保证对于任意一个状态和行动，我们都能得到对应的价值。因此在这种情况下，传统的方法，比如Q-Learning就无法在内存中维护这么大的一张Q表。

　　针对上面的问题，于是有人提出用一个模型来表示状态，动作到值函数的关系。我们令状态为 $s \in S $，行动为 $a \in A $，引入一个状态价值函数 $\hat{v}$，函数的参数为 $w$，接收状态 $s$ 的输入，则有：

　　　　$ \hat{v}(s, w) \approx v_{\pi}(s) $

　　对于动作-状态价值函数也是一样可以表示为：

　　　　$ \hat{q}(s,a,w) \approx q_{\pi}(s,a) $

　　还有一种表现形式是输入状态向量 $s$，输出每个动作 ${a_i}\in{A}$ 所对应的 $\hat{q}(s,a_i,w) $。具体的如下如所示：

　　

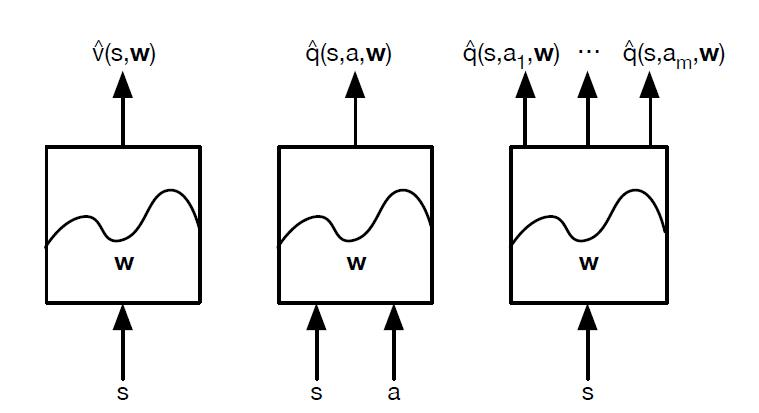
　　虽说有上面三种表达形式，但一般我们用第三种方式，这一种方法会获得所有动作的Q值，这样就可以很方便的使用贪婪策略和$\epsilon-greedy$。

　　现在的问题是我们该用什么样的函数来表作为价值函数呢？最简单的就是线性函数，用 $\phi(s)$ 表示状态 $s$ 的特征向量，则此时我们的状态价值函数可以表示为：

　　　　$ \hat{v}(s, w) = \phi(s)^Tw$

　　除了线性表示还可以用非线性函数来表示，最常用的非线性表示就是神经网络，在神经网络中可以使用DNN，CNN，RNN。

2 Deep Q-Learning 算法

　　Deep Q-Learning 算法简称DQN，DQN是在Q-Learning的基础上演变而来的，DQN对Q-Learning的修改主要有两个方面：

　　1）DQN利用深度卷积神经网络逼近值函数。

　　2）DQN利用了经验回放训练强化学习的学习过程。

　　我们现在来具体看看这两个方面：

　　1）DQN的行为值函数是利用神经网络逼近，属于非线性逼近，DQN所用的网络结构是三个卷积层加两个全连接层。用公式表示的话，值函数为$Q(s, a; \theta)$，此时更新网络其实就是更新参数 $\theta$，一旦$\theta$定了，网络参数就定了。

　　2）DQN最主要的特点是引入了经验回放，即将一个五元组 $(s_j, a_j, R_j, s'_j, {is\_end}_j)$ 添加到一个经验池中，这些五元组之后将用来更新Q网络参数，在这里$s_j$ 和$s'_j$ 都是向量的形式，动作和奖励是标量，$is\_end$是布尔值。

　　接下来我们看看整体训练步骤：

　　假设迭代轮数为EPISODES，采样的序列最大长度为L，学习速率为$\alpha$，衰减系数为$\gamma$，探索率$\epsilon$，状态集为S，动作集为A，批量梯度下降时的batch_size = m，经验回放池最大尺寸n。

　　1）for episode in range(EPISODES):   # 开始迭代

　　2）初始化状态s，在这里s为状态向量

　　3）for step in range(T):  # 序列采样

　　　　a) 在这里将状态向量$s$输入到$Q$网络中，采用${\epsilon}-greedy$ 获得动作$a$；

　　　　b) 在状态s下执行当前动作$a$，获得下一状态$s‘$，当前奖励$R$，是否终止状态${is\_end}$；

　　　　c) 将上面获得的五元组 $(s_j, a_j, R_j, s'_j, {is\_end}_j)$ 添加到经验回放池中：

　　　　　　A）判断若池子的大小大于m值，则从池子中批量采样并更新网络参数；

　　　　　　　　一）从经验回放池中随机采取m个样本 $(s_j, a_j, R_j, s'_j, {is\_end}_j)$ ，其中$j = 1, 2, 3....,m$，计算目标值$y_j$（若当作监督学习来看，可以将这个看作是样本的真实值）：

　　　　　　　　　　$y_j= \begin{cases} R_j& {is\_end_j\; is \;true}\\ R_j + \gamma\max_{a'}Q(s'_j, a'_j, w) & {is\_end_j \;is\; false} \end{cases}$

　　　　　　　　二）使用均方差损失函数 $\frac{1}{m}\sum\limits_{j=1}^m(y_j-Q(s_j, a_j, w))^2$ 更新$Q$网络参数（在这里$Q(s_j, a_j, w)$其实可以看作预测值，所以网络参数更新阶段和监督学习一样）。

　　　　　　B）判断若池子大小若大于n，则从池子中取出最早加入的五元组，添加新的五元组；

　　　　d) 对状态进行更新，$s = s'$;

　　　　e) 判断is_end是否是最终状态，若是循环结束，跳转到1），若不是继续循环采样。

　　看完整个流程之后再来回头看经验回放的作用：我们知道在训练神经网络的时候是假设训练数据是独立同分布的，但如果你采取当前参数下的网络获得的样本来更新当前的网络参数，那么这些顺序数据之间存在很强的关联性，网络的训练会很不稳定，现在利用经验回放的方法，你在更新当前时刻参数时会随机用到不同时刻参数下获得的样本，这样样本之间的关联性相对来说比较小。直接训练Q网络的好处是，只要Q值收敛了，则每个状态对应的最大动作也就确定了，也就是确定性的策略是已经确定了。

3 Nature DQN 算法

　　在上面的DQN中，我们可以看到在计算目标值$y_j$时和计算当前值用的是同一个网络$Q$，这样在计算目标值$y_j$时用到了我们需要训练的网络$Q$，之后我们又用目标值$y_j$来更新网络$Q$的参数，这样两者的依赖性太强，不利于算法的收敛，因此在Nature DQN中提出了使用两个网络，一个原网络$Q$用来选择动作，并更新参数，另一个目标网络$Q'$只用来计算目标值$y_j$，在这里目标网络$Q'$的参数不会进行迭代更新，而是隔一定时间从原网络$Q$中复制过来，因此两个网络的结构也需要完全一致，否则无法进行参数复制。

　　我们简单的从公式上介绍下和DQN算法的不同，在这里有两个网络$Q$和$Q'$，他们对应的参数分别是$w$和$w'$，在这里的更新频率可以自己设定，更新参数直接$w'=w$。

　　除此之外，我们还需要更改的就是目标值$y_j$的计算公式为：

　　　　$y_j= \begin{cases} R_j& {is\_end_j\; is \;true}\\ R_j + \gamma\max_{a'}Q’(s'_j, a'_j, w‘) & {is\_end_j \;is\; false} \end{cases}$

　　其余的和DQN完全相同。

4 Double DQN 算法

　　无论是DQN，还是Nature DQN都无法克服Q-Learning本身多固有的缺陷-过估计。

　　过估计是指估计得值函数比真实值函数要大，其根源主要在于Q-Learning中的最大化操作，从上面可以看到在动作选择中的目标是 $R_j + \gamma\max_{a'}Q’(s'_j, a'_j, w‘)$，其中的$max$操作使得估计的值函数比值函数的真实值大（注：对于真实的策略来说并在给定的状态下并不是每次都选择使得Q值最大的动作，因为一般真实的策略都是随机性策略，所以在这里目标值直接选择动作最大的Q值往往会导致目标值要高于真实值），为了解决值函数过估计的问题，Hasselt提出了Double DQN的方法，其定义是将动作的选择和动作的评估分别用不同的值函数来实现，而在Nature DQN中正好我们提出了两个Q网络。Double DQN也简称DDQN，其计算目标值$y_j$的步骤可以拆分为两步（针对$is\_end is False$这种条件）：

　　1）$a^{max}(s'_i, w) = \max_{a'}Q(s'_i, a, w) $  这一步是通过原网络Q获得最大值函数的动作$a$;

　　2) $y_j = R_j + \gamma Q'(s'_j, a^{max}(s'_i, w) , w‘) $  这一步是通过目标$Q'$网络获得上面的动作$a$对应的值。

　　将两个结合起来可以得到DDQN的目标值$y_j$的计算式：

　　　　$y_j= \begin{cases} R_j& {is\_end_j\; is \;true}\\ R_j + \gamma Q'(s'_j,\arg\max_{a'}Q(s'_j,a,w),w')& {is\_end_j\; is \;false} \end{cases}$

　　除此之外，其余的和Nature DQN一样

5 Prioritized Replay DQN 算法

　　在经验回放中是利用均匀分布采样，而这种方式看上去并不高效，对于智能体而言，这些数据的重要程度并不一样，因此提出优先回放（Prioritized Replay）的方法。优先回放的基本思想就是打破均匀采样，赋予学习效率高的样本以更大的采样权重。

　　一个理想的标准是智能体学习的效率越高，权重越大。符合该标准的一个选择是TD偏差$\delta$。TD偏差越大，说明该状态处的值函数与TD目标的差距越大，智能体的更新量越大，因此该处的学习效率越高。

　　优先回放DQN主要有三点改变：

　　1）为了方便优先回放存储与及采样，采用sumTree树来存储；

　　2）目标函数在计算时根据样本的TD偏差添加了权重（权重和TD偏差有关，偏差越大，权重越大）：

　　　　$\frac{1}{m}\sum\limits_{j=1}^m w_j (y_j-Q(s_j, a_j, w))^2$

　　3) 在这里TD误差的计算：$\delta_j = y_j- Q(s_j, a_j, w)$。因此每次更新$Q$网络参数时，都需要重新计算TD误差。

　　除了上面三点，其余的和DDQN一样，代码实现起来相对复杂，因为要构建sumTree，另外因为要计算的东西较多，而且每次都需要更新TD误差，因此算法的速度比较慢，个人感觉不是很好用，因此不做过多的介绍。

　　

6 Dueling DQN 算法

　　和前面所讲的各种DQN算法不同，Dueling DQN将整个模型结构分成了两个部分，一个为状态值函数，一个为优势函数，即：

　　　　$ Q^{\pi} (s, a) = V^{\pi} (s) + A^{\pi} (s, a) $

　　在这里状态值函数和动作无关，而且其也只会返回一个状态值，优势函数和动作和状态都有关。我们将上面的表达式细化，则有：

　　　　$ Q(s, a, w, \alpha, \beta) = V(s, w, \alpha) + A(s, a, w, \beta)$

　　即状态值函数和优势函数会共享一部分参数w，又各自有自己独有的参数$\alpha$和$\beta$。

　　Dueling DQN原则上可以和上面任意一个DQN算法结合，只需要将Dueling DQN的模型结构去替换上面任意一个DQN网络的模型结构。

　　但一般在使用中我们会对优势函数$A$做中心化处理：

　　　　$Q(s,a, w, \alpha, \beta) = V(s,w,\alpha) + (A(s,a,w,\beta) - \frac{1}{\mathcal{A}}\sum\limits_{a' \in \mathcal{A}}A(s,a', w,\beta))$