RenderTree渲染树

RenderTree渲染树对类中的静态成员有很重要的关系，这个和多态是有很重要的关系，举个简单的例子，在游戏中，马里奥需要渲染，蘑菇也需要渲染，怪兽也需要渲染，其是串在一个树上的，但是不同的类型怎么将其挂在一起，在渲染的过程中，马里奥，蘑菇和怪兽都是拥有不同的渲染接口，但是这样渲染器会做的很复杂，并不是我们想要的，简单的方式就是创建一个抽象基类，让马里奥，蘑菇和怪兽都继承同一个抽象基类，但是我们面临的问题是，对于马里奥，蘑菇和怪兽来说，他们的类型都是不一样的，怎么才能够穿在一个链表上

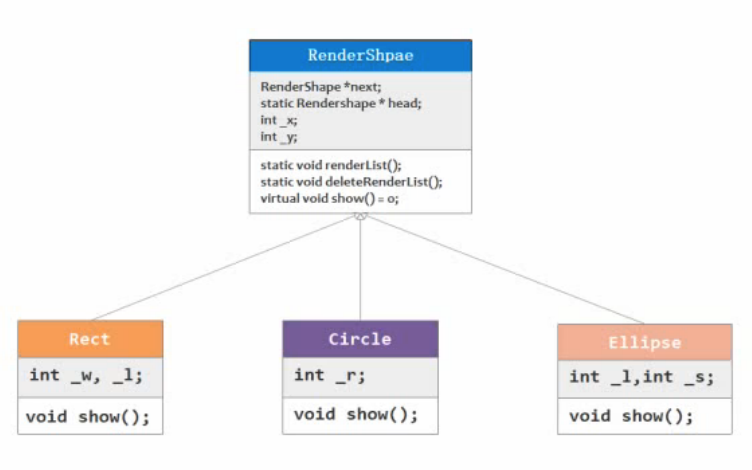
如上所示，提供一个纯虚函数show，使得下面的函数可以继承，每个子类中的show都是不一样的

为了将这些东西连起来，需要有个静态的头，这个是没有问题的

要串成一个链表，我们要求所有的节点都是类型是一样的，所以需要在每个节点加上next，因此这个链表本质上是父类指针next连在一起的

 #include <iostream>
 using namespace std;

 #include <thread>
 #include <unistd.h>
 //父类需要提供一个接口
 class RenderShape
 {
 public:
     virtual void show()=;
     bool init(int x,int y)
     {
         _x=x;
         _y=y;
         return true;
     }

     static void RenderShapeList()
     {
         RenderShape *t=head;
         while(t)
         {
             t->show();//所有的地方可以直接实现覆写
             t=t->next;
         }
     }

 protected:
     int _x;
     int _y;
     static RenderShape *head;//这个是需要共享的
            RenderShape *next;
 };

 RenderShape *RenderShape::head=nullptr;

 class Rect:public RenderShape
 {
 public:
     Rect *create(int x,int y,int w,int l)
     {
         Rect *pRet=new Rect;
         if(pRet&&pRet->init(x,y,w,l))
         {
             pRet->autoRelease();
         }
         else
         {
             delete pRet;
             pRet=nullptr;
         }
     }

     bool init(int x, int y,int w,int l)
     {
         RenderShape::init(x,y);
         _w=w;
         _l=l;
         return true;
     }

     void autoRelease()
     {
         this->next=head;
         head=this;
     }

     virtual void show()
     {
         cout<<"draw rect from"<<"("<<_x<<","<<")"<<_y
            <<"width"<<_w<<"length"<<_l<<endl;
     }
 protected:
     int _w;
     int _l;
 };

 class Circle:public RenderShape
 {
 public:
     Circle *create(int x,int y,int r)
     {
         Circle *pRet=new Circle;
         if(pRet&&pRet->init(x,y,r))
         {
             pRet->autoRelease();
         }
         else
         {
             delete pRet;
             pRet=nullptr;
         }
     }

     bool init(int x, int y, int r)
     {
         RenderShape::init(x,y);
         _r=r;
         return true;
     }

     void autoRelease()
     {
         this->next=head;
         head=this;
     }

     virtual void show()
     {
         cout<<"draw circle from"<<"("<<_x<<","<<")"<<_y
            <<"radius"<<_r<<endl;
     }

 protected:
     int _r;
 };

 class Ellipse:public RenderShape
 {
 protected:
     int _l;
     int _s;
 };

 void threadTask()
 {
     while()
     {
         cout<<"++++++++++++++++++++++++++"<<endl;
         RenderShape::RenderShapeList();
         sleep();
         cout<<"--------------------------"<<endl;
     }
 }
 int main()
 {
     Rect *pr;
     Circle *pc;

     thread t(threadTask);
     while()
     {
         int choice;
         cin>>choice;
         switch(choice)
         {
             case :
                 pr=Rect::create(,,,);
                 break;
             case :
                 pc=Circle::create(,,);
                 break;
         }
     }
     t.join();
     return ;
 }